5.2 Evolution Scenario

In all processes occurring in the universe, there are random factors (stochastic). They influence the development of processes and give them some uncertainty. The previous sections dealt with the probabilistic nature of the second law of thermodynamics. It is known that the laws of the microworld are described in the language of probability theory. The need to use probabilistic considerations to describe many of the laws of physics is an empirical generalization. Stochasticity permeates all levels of the organization of matter. For example, mutagenesis is a macro manifestation of the stochastic laws of the microworld. The identically flowing laws are absent, there is only a similarity, proximity. In other words, one cannot ignore the probabilistic nature of many processes occurring in the outside world, and the presence in them of many uncertain factors.

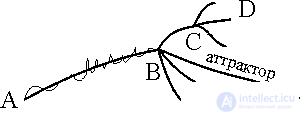
The analysis of dissipative systems considered in the previous chapter showed how self-organizing structures arise in a chaotic system, and revealed the role of fluctuations. When the system is unstable, a small fluctuation can grow to macroscales. The emergence of a new structure can take place along different trajectories of development: in such an environment there is potentially a range of structures (forms of organization). Their manifestation is determined by the internal properties of the medium. What has been said here allows us to give the following fairly universal scheme of the evolutionary process (Fig. 1). At the initial stage of development (segment AB) there is a slow change in the properties of the system; it is predictable up to random fluctuations that do not change the nature of development. At some point, B or external influences reach a critical value, or cumulation of internal influences occurs, at which the parameters of the system begin to change rapidly; a previously stable state loses its stability and the possibility of different paths of development arises. The evolutionary development of AB moves to completely new rails (point B). Its appearance is unpredictable, as is the further development of the system. Point B is called the bifurcation point. This concept is one of the main ones in universal evolutionism (bifurcation is a field of branching virtual paths of evolution). This term was introduced by the French physicist and mathematician Henri Poincare, he studied the various manifestations of the mechanism of bifurcation.

The bifurcation mechanism plays a crucial role in the overall evolutionary scheme; it is the source of the growth of the morphogenesis of various forms of matter.

Among the various branches of evolution after the bifurcation point B, there is a trajectory (or a rather narrow corridor of trajectories), which is distinguished by relative stability and, as it were, attracts all the multitude of trajectories of systems with different initial states. This trajectory is called an attractor (goal). If the system falls into this corridor (cone) of trajectories, then it inevitably evolves to this relatively stable state. 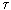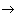The attractor can also be defined as the asymptotic limit ( 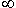) solutions, the limit on which the initial condition does not directly affect.

Due to the probabilistic nature of the bifurcation processes, evolution cannot have a reverse course, and this leads to irreversibility not only of evolution, but also of time.

In conclusion, we emphasize that chance is a creative, constructive beginning that can lead the system to an attractor, to one of its own environmental structures, to the internal tendency of its organization.

Here it is appropriate to present an important principle of the evolution of systems, which was formulated in a somewhat different form from each other by I. Prigogine and N. N. Moiseev: if the laws of conservation (matter, energy, momentum) allow several equilibrium states (solutions), then a state of motion is realized, which corresponds to the minimum increase in entropy.