Lecture
Before studying the main material, we recommend readers to become more familiar with the physical mechanisms of absorption and radiation.
For concreteness, we consider the scheme of a solid-state laser, for example, a ruby laser (Fig. 1).
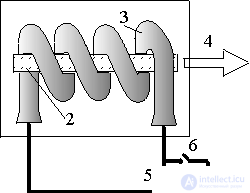
The housing 1 contains a ruby rod 2, on the ends of which there are mirrors; Using a xenon lamp 3, the ruby rod is optically pumped. Light of a xenon lamp is absorbed in the absorption bands of a ruby with wavelengths of 410 and 560 nm. From the end of a ruby rod with a translucent mirror, laser radiation 4 occurs with a wavelength of 694.3 nm. When the key 6 is closed from the power source 7, the capacitor 5 is charged; when this circuit is broken, a capacitor is discharged and then a pulsed radiation from a xenon lamp.
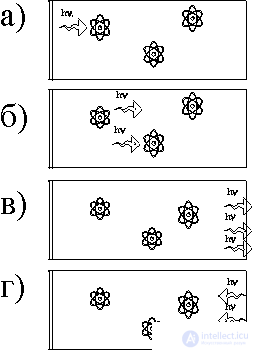 Figure 2. Generation of radiation in the active body:
Figure 2. Generation of radiation in the active body:
a) the photon interacts with the excited atom;
b) two photons appeared;
c) radiation from three atoms;
d) photons reflected from a translucent mirror end.
The radiation mechanism is schematically represented in fig. 2. Suppose that in the active body most of the atoms are in an excited state; they can be brought into this state in various ways - by optical pumping, due to collisions with electrons or excited atoms, and also due to the spontaneous emission of atoms. In fig. 2a shows three excited atoms (white circles); external photon with energy h  stimulates atom 1 to emit photon 2; further two photons move with energy h
stimulates atom 1 to emit photon 2; further two photons move with energy h  (Fig. 2b), which stimulate atom 2 to emit photon 3 with energy h
(Fig. 2b), which stimulate atom 2 to emit photon 3 with energy h  (Fig. 2c); Further, these three photons are reflected from a translucent mirror (Fig. 2d). Reflected photons travel along the rod the way back, and an increasing number of atoms populate a higher energy level.
(Fig. 2c); Further, these three photons are reflected from a translucent mirror (Fig. 2d). Reflected photons travel along the rod the way back, and an increasing number of atoms populate a higher energy level.
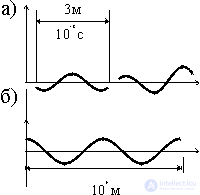
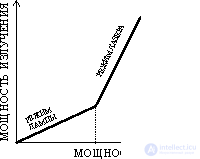
With a limited pump power, the laser works like a lamp — the emissions of individual atoms are not coordinated with each other and they emit wave trains of several meters in length (Fig. 3a). At a certain critical value of the pump power, the power of laser radiation sharply increases. A coordinated, cooperative emission of waves that are in the same phase occurs, and the length of the wave trains increases to 10 9 m (Fig. 3b). The transition from the lamp radiation mode to the laser mode occurs (Fig. 4).
Prior to the development of the laser in 1960, all radiation available to mankind in the ultraviolet, visible and infrared regions of the spectrum was incoherent. We note the features of laser radiation: monochromaticity ( 
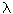 ~ 0.1
~ 0.1 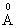 ); high temporal and spatial coherence; high intensity; the narrowness of the beam (from the Earth to the Moon is 360000 km, and the beam expansion is only 3 m).
); high temporal and spatial coherence; high intensity; the narrowness of the beam (from the Earth to the Moon is 360000 km, and the beam expansion is only 3 m).
We offer readers to get acquainted with the mathematical model of the laser.
The generation of coherent radiation with the help of a laser produced a revolution in one of the most well-established branches of physics - optics. It was shown that this phenomenon can be regarded as a kind of self-organization process that occurs under non-equilibrium conditions.
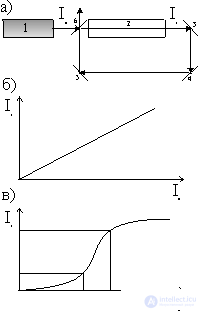 Figure 5. Optical bistability.
Figure 5. Optical bistability.
a) Diagram of the experimental device: 1 - laser; 2 - nonlinear medium; 3, 4, 5 - mirrors, 6 - a translucent mirror.
b) Dependence of the intensities of transmitted and incident light in an empty cavity.
c) the same for the optically active medium.
Consider the concept of using the phenomenon of optical bistability for the implementation of an optical computer. In fig. 5a is a schematic representation of a device for observing optical bistability. From laser 1, a beam of light with intensity I 0 passes through optical medium 2 and exits with intensity I 1 . At the expense of a certain position of the mirrors 3-6, part of the light returns to Wednesday 2 (positive feedback). If medium 2 were empty, then the dependence I 1 = f 1 (I 0 ) would have the form shown in Fig. 5 B. Fill cavity 2 with optical material and note that the interaction of the substance with the light is non-linear in the presence of the resonance of the substance with the incident beam. Then, on some part of the curve I 1 = f 2 (I 0 ), an amplification occurs (Fig. 5c). The system acquires the properties of an optical transistor. There are conditions under which the dependence I 1 = f 3 (I 0 ) of the system behavior is characterized by the presence of bistability: two (sometimes several) stable stationary states can occur (Fig. 6).
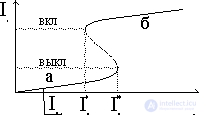
At some value of the parameter 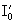 , there is only one steady state (branch a). Increasing I 0 , we enter the area of multiple states
, there is only one steady state (branch a). Increasing I 0 , we enter the area of multiple states 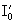 <I 0 <
<I 0 < 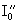 . However, the system remains on branch a until I 0 exceeds the values
. However, the system remains on branch a until I 0 exceeds the values 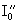 after which a jump-like transition occurs to branch b, on which the system remains. If we now change I 0 in the opposite direction, then the system will be on branch b up to the values
after which a jump-like transition occurs to branch b, on which the system remains. If we now change I 0 in the opposite direction, then the system will be on branch b up to the values 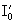 . Two transmission levels can be brought into correspondence with the logical states "0" and "1", i.e., to build on this basis an element of "optical memory" or "optical switch".
. Two transmission levels can be brought into correspondence with the logical states "0" and "1", i.e., to build on this basis an element of "optical memory" or "optical switch".
Comments
To leave a comment
Synergetics
Terms: Synergetics