Lecture
The remains of the Austrian physicist Boltzmann (1844-1906) rest in the central cemetery of the city of Vienna. On his gravestone is engraved a formula that bears his name:
The parameter S - entropy - serves as a measure of the scattering of the energy of the Universe, and P - characterizes any spontaneous changes, this value refers to the world of atoms that determine the hidden mechanism of change. Thus, formula (1), the derivation of which is given separately, associates entropy with chaos.
Under equilibrium conditions, entropy is a function of the state of a system that can be measured or calculated theoretically. But if an isolated system deviates from equilibrium, the property of entropy arises - it only increases.
Imagine the formula (1) in the form
and pay attention to the fact that the statistical weight of the state of the system P grows exponentially with increasing S. In other words, a less ordered state (greater chaos) has a greater statistical weight * , since it can be implemented in more ways. Therefore, entropy is a measure of system disorder.
Due to random rearrangements, there is a growing mess on the table, in the room. The order is created artificially, the disorder is spontaneous, since it is answered with a high probability, a large entropy. Reasonable human activity is aimed at overcoming disorder.
Let's pay attention to the fact that the first law of thermodynamics (energy conservation law) is an absolutely strict law, it is a deterministic law. The second law of thermodynamics, the law of entropy increase, is a statistical (probabilistic) law.
There is even a possibility that molecules located in a 1 cm 3 cube may all gather in one half of this cube. The probability for one molecule to be in the right side of the cube: q 1 = 1/2. Under normal conditions, 1 cm 3 contains the number of molecules 2.7 * 10 19 (the number of Loshmidt), then the probability that all molecules will gather in the right half of the cube is equal to  . This is vanishingly small.
. This is vanishingly small.
Boltzmann's work is a breakthrough in a completely new field: probability has entered into physics, statistical laws. This means that although rarely, the entropy may also decrease.
In the state of equilibrium occurs in the system of equalization of temperatures T, densities 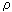 and s
and s 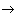 S max , i.e., the system is in the state of maximum possible heterogeneity. However, there may be deviations from the most likely temperature
S max , i.e., the system is in the state of maximum possible heterogeneity. However, there may be deviations from the most likely temperature 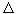 T, condensation and gas dilution (
T, condensation and gas dilution ( 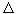 r). These deviations are called fluctuations. They are the less likely, the greater the number of molecules. Recall (output) the distribution of N molecules in two boxes.
r). These deviations are called fluctuations. They are the less likely, the greater the number of molecules. Recall (output) the distribution of N molecules in two boxes.
Calculate the distribution in two boxes for 2; four; 6; ...; 12 molecules. The results are presented in table 1.
The table shows how the nature of the distribution changes with an increase in the number of particles N: the larger the N, the sharper the distribution, i.e., the lower the probability of the extreme distributions. When N = 2, the statistical weight of the state in which all the molecules are collected, for example, in the left box is only two times smaller than the state with a uniform distribution. With N = 12, this ratio is no longer 1: 2, but 1: 924. So, the probability of a noticeable deviation from the most probable state decreases with increasing N. These deviations are fluctuations * .
With a large number of molecules, the number of ways of their uniform distribution in two boxes is equal to

Approximate expression is obtained according to the Stirling formula [1].
Comments
To leave a comment
Synergetics
Terms: Synergetics