Lecture
If several irreversible processes take place at the same time, then in an open system these processes are connected with each other: the flows J 1 and J 2 depend on the forces X 1 and X 2 , i.e.
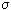 = J 1 X 1 + J 2 X 2
= J 1 X 1 + J 2 X 2 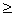 0 but
0 but Here L 11 , L 12 , L 21 , L 22 are the coefficients of proportionality.
These equations are linear, which is the case for systems that are close to equilibrium, with the relation
With small deviations from the equilibrium state between the flows and forces there are linear dependencies. For example, the mass flow j [kg / (m 2. s)] is associated with the gradient of concentration grad C dependence (Fick's law):
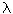 grad T,
grad T, 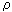 ) grad j.
) grad j. In these equations D, 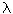 , (one/
, (one/ 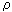 ) - diffusion coefficients, thermal conductivity and electrical conductivity.
) - diffusion coefficients, thermal conductivity and electrical conductivity.
If several irreversible processes take place simultaneously, then in an open non-equilibrium system these processes are associated with each other and can lead to the appearance of new effects. For example, thermoelectricity appears from the superposition of thermal and electrical conductivities, while diffusion and thermal conduction are superimposed - thermal diffusion.
Consider some examples. In the case of thermal diffusion, the fluxes of matter (- D grad C) and thermal energy (- 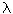 grad T) are conjugate
grad T) are conjugate
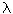 grad T, (2)
grad T, (2) 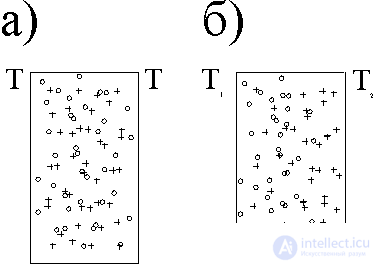
In fig. 1a, a mixture of gases in a vessel is presented, the walls of which have the same temperatures T, the mixture is in equilibrium and S = S max . If the walls of the vessel receive different temperatures T 1 and T 2 , then a process of thermal diffusion will occur. At the same time, lighter molecules (greater mobility) tend to move to warm regions, and heavy molecules - to cold ones (Fig. 1, b) - the Soret effect. With a constant temperature gradient, a steady-state concentration gradient is established. At the same time with thermal diffusion, which causes partial separation of the mixture, oppositely directed gradient diffusion appears, which tends to equalize the concentration. Note that the loss of entropy during the separation of gases (a larger order - less entropy) overlap with its gain due to thermal conductivity. Consequently, it is possible to implement a process that goes with a decrease in entropy as a result of conjugation with an entropy profitable process.
Consider thermoelectric phenomena in isotropic bodies.
- Seebeck effect: at the junction of two different conductors having a temperature difference  t occurs EMF E =
t occurs EMF E = 
 t (
t ( 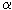 - coefficients TEDS). Therefore, if from two different conductors to make a closed circuit and the contact points to support when
- coefficients TEDS). Therefore, if from two different conductors to make a closed circuit and the contact points to support when 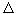 t, then an emf arises in the circuit.
t, then an emf arises in the circuit.
- Peltier effect: when electric current passes through such a circuit, Peltier heat, which is proportional to the amperage, is released or absorbed at such a junction.
- Thomson effect: when electric current passes through such a circuit, in addition to Joule heat, additional heat is generated, which is proportional to the temperature gradient.
Under the joint action of electrical and thermal processes, heat flux q and electricity j are conjugated
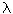 qrad t - П j, (3)
qrad t - П j, (3) 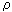 ) qradj +
) qradj + 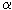 qrad t,
qrad t, 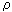 and
and 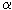 - electrical resistivity and TEC.
- electrical resistivity and TEC. Dependencies (2) - (3) can be represented in the form of an equation, which can be generalized for many processes:
the flow J i , caused by the action of the forces X c , is proportional to these forces
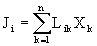 ,
, where L ik - coefficients of proportionality to these forces (thermal conductivity, diffusion, electrical conductivity, thermal electric potential, Peltier and others). Onsager's theorem (1) for many forces will take a general view
This dependence means that there is a symmetry in the interaction of various processes. For example, if qrad T causes a concentration gradient, the latter generates a temperature gradient.
Comments
To leave a comment
Synergetics
Terms: Synergetics