Skeletoning methods

The second important family of path planning algorithms is based on the concept of skeletonization . These algorithms reduce the free space of the robot to a one-dimensional representation, for which the scheduling task becomes easier. Such a representation with a smaller number of dimensions is called the skeleton of the configuration space.

An example of the use of the skeletonization method is shown in the figure: this is the Voronoi line for free space, which is the geometric locus of all points equidistant from two or several obstacles. In order to plan the path using the Voronoi line, the robot first moves from the current configuration to a point on the Voronoi line. It can easily be shown that such an operation can always be performed by moving in a straight line in the configuration space. Then the robot follows the Voronoi line until it reaches the point closest to the target configuration. Finally, the robot leaves the Voronoi line and moves to the target. And at this last stage, the movement in a straight line in the configuration space is performed again.

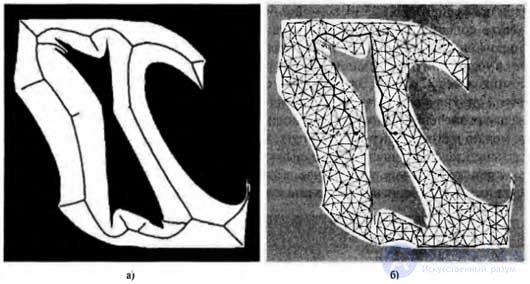
One example of the skeletonization method: the Voronoi line is the locus of points equidistant from two or more obstacles in the configuration space (a); probabilistic roadmap consisting of 400 randomly selected points in free space (b)

Thus, the initial task of planning a path is reduced to finding a path on the Voronoi line, which is usually one-dimensional (with the exception of some special cases) and has a finite number of points at which three or more one-dimensional curves intersect. Movement along the Voronoi line may not provide the shortest path, but the paths detected will be distinguished by the presence of maximum distances from obstacles. The drawbacks of the methods based on the use of the Voronoi line are that they are difficult to apply in configuration spaces with large dimensions, moreover, when using them, one has to perform too large detour maneuvers if the configuration space has a wide scope. In addition, it may be difficult to calculate the Voronoi line, especially in the configuration space, which is characterized by a complex form of obstacles.

An alternative to the Voronoi line based method is a method using a probabilistic roadmap . It represents such an approach to skeletonization, which allows you to identify more possible routes and therefore is better suited for spaces with a wide scope. An example of a probabilistic roadmap is shown in Figure b). The line shown in this figure was created by forming a large number of configurations at random and removing those that do not fit into the free space. After that, any two nodes are connected by some line, if one of them can be “easily” reached from the other; for example, if in free space you can go from one node to another in a straight line. The final result of all these operations is the creation of a randomized graph in the free space of the robot. If the positions of the initial and target configurations of the robot are added to this graph, then the task of planning the path will be reduced to a search in a discrete graph. Theoretically, this approach is incomplete, because if the randomly given points are chosen unsuccessfully, it may be impossible to find a single path from the initial node to the target. But the likelihood of such a failure can be limited by regulating the number of formed points and taking into account certain geometric properties of the configuration space. It is also possible to direct the process of generating control points to those areas where a partially completed search shows good prospects for finding an acceptable path, acting in two directions simultaneously, from the initial and from the target positions. After making all these improvements, the planning method using a probabilistic roadmap shows better scalability in multidimensional configuration space conditions compared to most other alternative path planning methods.