Reliable methods

Uncertainty can also be dealt with using so-called robust rather than probabilistic methods. A reliable method is one that implies a limited amount of uncertainty in every aspect of the problem, but the probabilities are not assigned to values ​​within the allowed interval. A reliable solution is defined as such a solution that leads to the intended target, regardless of what data values ​​occur in reality, provided that they are within the intended interval. An extreme form of a reliable method is a compatible planning approach — it develops plans that can be accomplished even without state information.

We consider one of the reliable methods used for planning thin movements (or abbreviated FMP - Fine-Motion Planning) in the tasks of a robotic assembly. Planning for subtle movements provides movement of the robot arm in very close proximity to the object in a static environment. The main difficulty associated with planning for subtle movements is that the required movements and the corresponding characteristics of the environment are very small. On such a small scale, the robot loses the ability to accurately measure or control its position; in addition, uncertainty may arise regarding the shape of the medium itself; It is assumed that all these uncertainties are limited. The solution of the FMP problem usually becomes a conditional plan (or policy), which uses feedback from the senders and which guarantees successful execution in all situations compatible with the estimated limits of uncertainty.

The plan for conducting subtle movements is the definition of a number of protected movements. Each protected movement consists, firstly, of the movement command and, secondly, of the termination condition, which is a predicate defined on the sensory values ​​of the robot, and returns the true value as an indication of the end of the protected movement. Motion commands typically specify adaptable movements that allow the robot to perform gliding movements if other movement commands cause a collision with an obstacle. As an example, Figure 1 shows a two-dimensional space of configurations with a narrow vertical opening. Such a space of configurations can arise when solving the problem of inserting a rectangular peg into the hole, which is slightly larger than it. Motion commands are performed at constant speeds. Termination conditions are surface contact situations. To simulate uncertainty in the control process, let us assume that the robot actually moves not in the direction indicated in the command, but fits into the cone C _v around this direction. Figure 1 shows what happens if a constant speed command is given strictly in the vertical direction from the source area s . Due to the uncertainty in speed, the robot can move in any direction within the conical envelope; It is possible that this will lead to a hole in the hole, but it is more likely that the peg will fall on one side or the other. And since the robot will not have information on which side of the hole the peg has dropped, it will not know where to move it further.

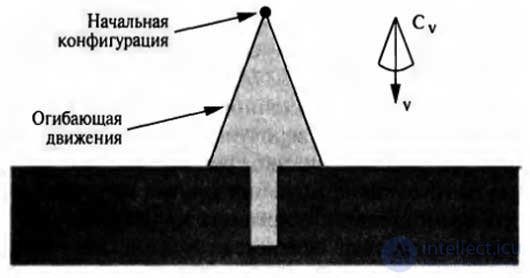
Figure 1. Two-dimensional environment, a cone of velocity uncertainty and the envelope of possible robot movements. The target speed is equal to v , but due to uncertainty, the actual speed can be within C _v , and this leads to the fact that the final configuration can be determined at any point within the envelope of the movement. This means that uncertainty arises as to whether or not it will be able to get into the hole.

A more acceptable strategy is shown in Figure 2 and 3. In Figure 2

An example of how the robot intentionally directs its movement in a certain direction from the hole is given. The conditions for executing a movement command are shown in the figure, and contact with any surface becomes the verification of the end of movement. Figure 3 shows that a motion command is issued that forces the robot to move the peg that slides along the surface before it enters the hole. Thus, the use of the adaptable movement command is assumed. Since all possible speeds in the envelope are directed to the left, the robot must move the peg sliding on the surface to the right after it comes into contact with the horizontal surface. Following the touch of the peg with the right vertical wall of the hole, the peg should slide down, since all possible speeds are directed downward relative to this vertical surface. The peg will continue to move until it reaches the bottom of the hole, since that is the condition for the completion of this movement. Despite the uncertainty of control, all possible trajectories of the robot's movement end in contact with the bottom of the hole, of course, provided that no surface defects are found that make the robot unable to move the stuck peg.

Figure 2. First 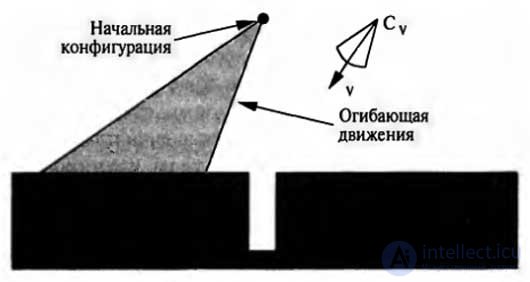I am a team of movement and the resulting envelope of possible movements of the robot. Regardless of any errors, it is known that in the final configuration the peg will be to the left of the hole

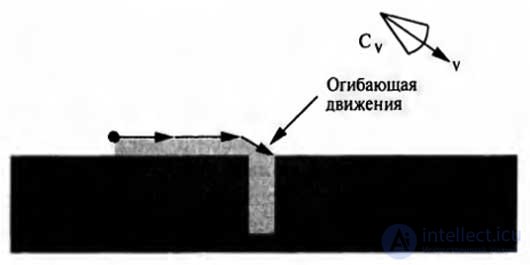
Figure 3. Second movement command and envelope of possible movements. Even with inaccuracies, the peg ends up in the hole

It is quite obvious that the task of constructing plans for subtle movements is not trivial; in fact, it is much more complicated than the task of planning in terms of precise movements. To solve this problem, you can either choose a constant number of discrete values ​​for each movement, or use the geometry of the medium to select directions that allow you to determine a qualitatively different behavior. The Planner of Thin Motions takes as input the description of the configuration space, the angle of inclination of the cone of velocity uncertainty, and the specification of possible sensory perceptions that determine the termination situation (in this case, contact with the surface). In turn, the planner must develop a multi-stage conditional plan (or policy), allowing to achieve guaranteed success, if such a plan exists.

In this example, it is assumed that the scheduler has at its disposal an exact model of the environment, but it is also possible to accept the assumption that there is a limited error in this model, as shown below. If the error can be described in terms of parameters, then the corresponding parameters are added as degrees of freedom to the configuration space. In particular, in the last example, if there were uncertainties regarding the depth and width of the hole, then these values ​​could be added to the configuration space as two degrees of freedom. It does not follow from this that it will be possible to move the gripper of the robot directly in the direction of these degrees of freedom in the configuration space or to receive information about their position. But both of these limitations can be taken into account by describing the task as an FMP task, setting the data on the uncertainties of the controls and sensors accordingly. The result is a complex, four-dimensional planning task, but it is possible to use exactly the same planning methods as before. It should be noted that a reliable approach of this kind leads to the creation of plans that take into account the results of the most unfavorable developments, rather than maximizing the expected quality of the plan, unlike the methods of the theory of solutions. The only optimal aspect of action plans in the most unfavorable situation (from the point of view of the theory of solutions) is that they allow you to prevent the consequences of failure during the execution of the plan, much worse than any other costs associated with its implementation.