Lecture
Reducing the mass of radio-electronic devices is of great importance for the expansion of opportunities to meet the information needs of society. In many cases, the mass (dimensions) of a radio electronic device is crucial for its application possibilities. Particularly critical are the requirements for the mass of electronic devices when they are used on airplanes, rockets, satellites.
If the mass of the onboard RES exceeds a certain level, then the meaning of their installation is lost, since the payload mass (passengers, scientific equipment) for which an airplane, a rocket, an AES is created is unacceptably reduced. Of course, it is possible to increase the capacity of the carrier, its carrying capacity, etc. But, at the same time, it is necessary to significantly increase their mass in comparison with the RES.
In tab. 3.2 given the change 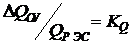 for different carriers where
for different carriers where 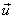 - increase in the mass of the installation object (carrier), necessary to save its parameters during the installation of the electronic device;
- increase in the mass of the installation object (carrier), necessary to save its parameters during the installation of the electronic device; 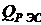 - mass RES;
- mass RES; 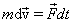 - coefficient of weight increase.
- coefficient of weight increase.
The expediency of reducing the mass of radio electronic devices is obvious, especially since often microminiaturization leads to an increase in processability and lower cost. However, sometimes a decrease in OEP leads to an increase in their cost, for example, when using custom-made LSIs, gilded contacts, microminiature ERE, in which expensive materials are used, as well as a decrease in the yield. It should be borne in mind that for airborne RESs, it is usually justified to reduce the mass of the RESs even when costs increase. Consider the optimization of the total cost of the RES and the carrier in connection with the increase in its mass and cost during the installation of the RES. Increment the cost of the media when installing RES:
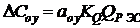 (3.3)
(3.3)
Where 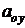 - proportionality coefficient, showing the cost per kilogram of carrier.
- proportionality coefficient, showing the cost per kilogram of carrier.
We will get the costs for the EFEs, assuming that they increase with decreasing mass. Suppose that the inverse proportion is true. Then
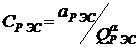 (3.4)
(3.4)
Where 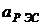 - coefficient reflecting the increase in the cost of RES with their complexity; a - the exponent, reflecting the rate of change in the cost of RES with a change
- coefficient reflecting the increase in the cost of RES with their complexity; a - the exponent, reflecting the rate of change in the cost of RES with a change 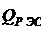 . Then total costs
. Then total costs 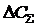 are equal:
are equal:
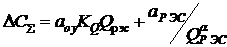
Differentiating on Q RES and equating the derivative to zero, we find the mass of the RES, which gives the minimum cost for the carrier and the RES when installing the RES:
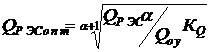 (3.5)
(3.5)
Let us assume that the complex of the airplane RES has an initial weight of 300 kg and costs 10 5 rubles. Then, for a = 1, arc = 3 10 7 rubkg. The optimal mass of the RES in the assumption of fairness (4) with a oy = 100rub / kg, K Q == 15 will be
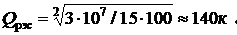
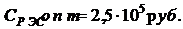
Therefore, to reduce the total cost, it is advisable to redesign the RES to allow for an increase in manufacturing costs by about two times (for example, by increasing the degree of integration and using custom-made LSIs; most compact connectors, etc.).
Comments
To leave a comment
Design and engineering of electronic equipment
Terms: Design and engineering of electronic equipment