Shortcut Search Algorithms

In the shortest path problem (shortest-paths problem), we set a weighted oriented graph G = (V, E) with the weight function w: E -> R, which reflects edges on their weights, whose values ​​are expressed by real numbers. The weight (weight) of the path p = (Vo, Vi, ..., Vk) is equal to the total weight of the edges included in it.

The weight of the shortest path (shortest-path weight) from the top and to the top v is determined by the ratio

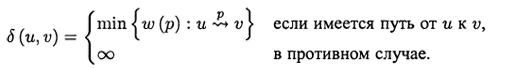
Then, by definition, the shortest path (shortest path) from the vertex and to the vertex v is any path whose weight satisfies the relation w (p) = delta (u, v).

The weight of each of the edges can be interpreted not as a distance, but as a different metric. Often they are used to represent time intervals, cost, fines, losses, or any other value that linearly accumulates as one moves along the edges of the graph and which should be kept to a minimum.

The algorithm allows to solve many other problems, including those listed below.

1) The problem of the shortest path to a given destination (single-destination shortest-paths problem). It is required to find the shortest path to the given destination vertex t, which starts at each of the vertices v. By changing the direction of each edge belonging to the graph, this problem can be reduced to the problem of a single initial vertex.

2) The problem of the shortest path between a given pair of vertices (single-pair shortest-paths problem). It is required to find the shortest path from the given vertex u to the given vertex v. If the problem of a given initial vertex u is solved, then this problem is also solved.

3) The problem of the shortest path between all pairs of vertices (all-pairs shortest-paths problem). It is required to find the shortest path from each vertex u to each vertex v. This problem can also be solved using an algorithm designed to solve the problem of a single source vertex, but usually it is solved faster.

This section presents the Bellman-Ford algorithm, which allows to solve the problem of the shortest path from a fixed source in the general case when the weight of any edge can be negative. This algorithm is notable for its simplicity. Its advantages also include the fact that it determines whether the graph contains a negative-weight cycle reachable from the source. The section also describes the Dijkstra algorithm, which is characterized by a shorter execution time than the Bellman-Ford algorithm, but requires that the weight of each of the edges be non-negative. In addition, a dynamic programming algorithm is given - the Floyd-Warshall algorithm (Floyd-Warshall), which allows solving the problem of finding the shortest paths between all pairs of vertices.