New Year's party decision through graphs

USA Computing Olympiad, 2002

The task

A group of N (1

The cow party coordinator wants to maximize the total number of dishes that will be brought to the party, but has a fixed limit on the number of dishes of each type. Each cow can bring K (1 <= K <= 5) dishes, but they must be different from each other. For example, one cow cannot bring 3 beef patties, but can bring a pie, bread and delicious alfalfa in an orange sauce. What is the maximum amount of food that cows can bring to the party?

Input

Line 1: Three integers: N, K, D
Line 2: D non-negative numbers - the limit of the total quantity for each of the various dishes that can be brought to the party.
Lines 3..N + 2: Each line contains an initial integer Z (1 <= Z <= D), denoting the number of types of different dishes that one cow can cook; the remainder of the line contains Z integers - identifiers of the types of food that a cow can prepare, corresponding to the current line (in line 3 - cow 1, in line 4 - cow 2, etc.).

  Input example [ party.in ] file: 
 4 3 5 
 2 2 2 2 3 
 4 1 2 3 4 
 4 2 3 4 5 
 3 1 2 4 
 3 1 2 3 

  Data Explanations 
 4 3 5 4 cows, each up to 3 courses, a total of 5 different types of food 
 2 2 2 2 3 max - 2 dishes of types 1..4 and 3 dishes of type 5 
 4 1 2 3 4 1st cow can cook 4 different dishes A, 2, 3, 4) 
 4 2 3 4 5 The 2nd cow can cook 4 different dishes B, 3, 4, 5) 
 3 1 2 4 The 3rd cow can cook 3 different dishes A, 2, 4) 
 3 1 2 3 4th cow can cook 3 different dishes A, 2, 3) 

Conclusion

One line contains one integer - the maximum number of dishes that can be brought to the party.

Example output:
9

Explanations:
Cow 1 will bring dishes 3 and 4:
Cow 2 will bring dishes 3. 4 and 5:
Cow 3 will bring dishes 1 and 2;
Cow 4 will bring dishes 1 and 2.

Solution [up]

Consider a graph consisting of N + D vertices. Vertices with numbers from 1 to N correspond to cows, vertices with numbers from N + 1 to N + D correspond to different types of food (dishes).

First of all, we must add a source to the vertex graph (vertex with number start = N + D + 1) and drain (vertex with number Finish = N + D + 2). It is clear that from the source there should be arcs to all vertices 1..N (cows), and from the vertices N + 1..N + D (dishes) there should be arcs to drain. What should be the weights of the arcs introduced from the source and to the drain? For source “arcs”: c [start, i] - K (for all i from 1 to N), since each cow can bring K to dishes. For “to drain” arcs: c [i, Finish] - Lim [iN] (for all i from N + 1 to N + D), since there is a limit on the number of dishes of each type.

We build an arc from cow i to dish j if and only if cow i can cook dish j. The weight of each arc should be set to 1, since the dishes that the cow will bring must be different from each other.

Next, using the Ford-Fulkerson algorithm, we find the maximum flow from the source (top start) to the drain (top finish). The value of the maximum flow will be the desired value of the number of dishes.

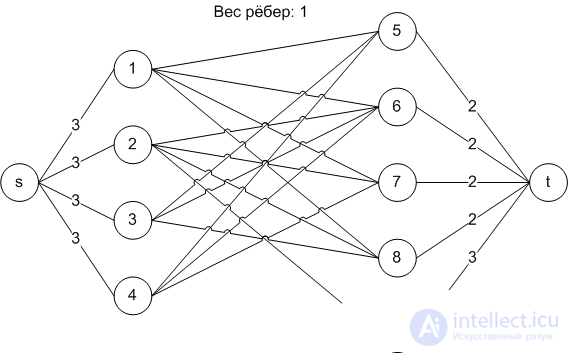
The graph obtained for this task

Formal description [up]

  Party ()
 1. Read the task input data from the file.
 2. Create a vertex-source and connect it with the vertices of the graph, which 
    meet the cows.  The throughput for these edges is 
    the value of the limit on the dishes for each cow.
 3. Create a top-drain and connect it with the tops-dishes. 
    The capacity is equal to the limit for each dish.
 4. Find the maximum flow for the Ford-Fulkerson algorithm between the source 
    and drain.
 5. Find dishes cooked by each cow.
 6. Count the number of different dishes.