Prima algorithm

The Prima algorithm is an algorithm for constructing a minimal spanning tree of a weighted connected non-oriented graph. The algorithm was first discovered in 1930 by the Czech mathematician Wojciech Jarnik, later rediscovered by Robert Prim in 1957, and, independently of them, by E. Dijkstra in 1959.

The Prima algorithm has the property that the edges in the set A always form a single tree. The tree starts from an arbitrary root vertex r and grows until it covers all vertices in V. At each step, a light edge is added to tree A, connecting the tree and a separate vertex from the rest of the graph. This rule adds only A-safe edges; therefore, upon completion of the algorithm, the edges in A form a minimal spanning tree. This strategy is greedy, because at each step an edge is added to the tree, which makes the minimum possible contribution to the total weight.

The input data to the algorithm are the connected graph G and the root r of the minimal spanning tree. All vertices of G that have not yet fallen into the tree are stored in a queue with priority Q. The priority of vertex v is determined by the value key [v], which is equal to the minimum weight of the edges connecting v with the vertices of the minimum skeleton. The prev [v] field for the tree vertices indicates the parent, and for the vertices from the queue, it indicates the tree vertex into which the edge leads with the weight key [v] (one of these edges, if there are several).

Formal description

  MST_PRIM (G, w, r)
 1 for (For) each vertex u є V [G]
 2 do key [u] "- INFINITY
 3 prev [u] "- NIL
 4 key [r] "- 0
 5 Q "- V [G]
 6 while Q is not empty
 7 do u "- Extract_Min (Q)
 8 for (For) each vertex v є Adj [u] 
  9 do if v є Q and w (u, v) < key [v]
 10 then prev [v] "- u
 11 key [v] "- w (u, v)

In lines 1-5, the keys of all vertices are set equal to INFINITY (except for the root r, the key of which is 0, so that it turns out to be the first vertex to be processed), parent signs for all nodes are assigned NIL values ​​and all vertices are entered in the queue with priorities Q. The algorithm supports the following cycle invariant, consisting of three parts.

Before each iteration of the while loop in lines 6-11

1. A = {(v, prev [v]): v є V - {r} - Q};
2. the vertices already placed in the minimum spanning tree belong to the set V - Q;
3. for all vertices v є Q the following is true: if prev [v]! = NIL, then key [v]

Line 7 defines a vertex and belonging to a light edge intersecting the cut (V - Q, Q) (except for the first iteration, when and = r according to the assignment in line 4). Deleting and from the set Q adds it to the set V - Q of tree vertices. The for loop in lines 8-11 updates the key and prev fields for each vertex v adjacent to u and not in the tree. This update saves the third part of the invariant.

Complexity assessment

The operation time of the Prim algorithm depends on the chosen implementation of the queue with priorities Q. If you implement it as a binary pyramid, then it will take O (V) time to perform the initialization in lines 1-5. The body of the while loop is executed | V | times, and since each Extract_Min operation takes O (lg V) time, the total time of all Extract__Min procedure calls is O (V * lg V). The for loop in lines 8-11 is executed only O (E) times, since the sum of the lengths of all adjacency lists is 2 | E |. Inside the for loop, a check for Q belonging on line 9 can be implemented in constant time by using a bit for each vertex indicating whether it is in Q and updating this bit when deleting a vertex from Q. The assignment in line 11 implicitly includes the Decrease_Key operation over the pyramid. The execution time of this operation is O (lg V). Thus, the total operation time of the Prima algorithm is o (V * lg V + E * lg V) = o (E * lg V) , which asymptotically coincides with the time of the Kruskal algorithm.

Example

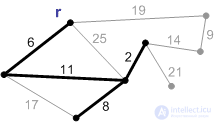
Execution of the Prima algorithm:

1. The initial phase. The minimal forest cover consists of a root and an empty set of edges.

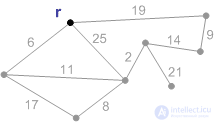
2. An edge with a weight of 6 is the minimum edge connecting the root to the other vertices. Add it to the minimum frame.

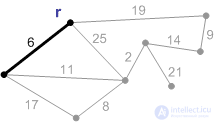
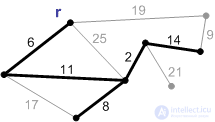
3. The next safe edge with a weight of 11. Add it.

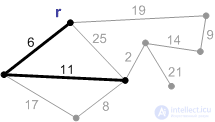
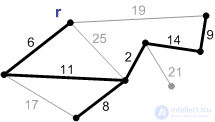
4-8. Add the rest of the safety edges.

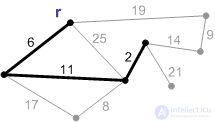
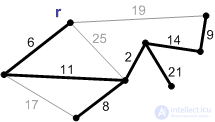
Ribs weighing 17, 19, and 25 are not safe. Their ends are in the same connected component. A rib with a weight of 21 is safe, so we add it. Minimum spanning tree built.

Evaluation

The asymptotics of the algorithm depends on the method of storing the graph and the method of storing vertices that are not in the tree. If the priority queue is {\ displaystyle Q} implemented as a regular array {\ displaystyle d} then {\ displaystyle Extract.Min (Q)} executed in {\ displaystyle O (n)} , and the cost of the operation is {\ displaystyle d [u] \ gets w (v, u)} makes {\ displaystyle O (1)} . If {\ displaystyle Q} is a binary pyramid, then the cost is {\ displaystyle Extract.Min (Q)} reduced to {\ displaystyle O (\ log n)} , and the cost is {\ displaystyle d [u] \ gets w (v, u)} increases to {\ displaystyle O (\ log n)} . When using the Fibonacci pyramid operation {\ displaystyle Extract.Min (Q)} running as {\ displaystyle O (\ log n)} and {\ displaystyle d [u] \ gets w (v, u)} for {\ displaystyle O (1)} .

The way to represent the priority queue and graph	Asymptotics
Array d, adjacency lists (adjacency matrix)	{\ displaystyle O (V ^ {2})}
Binary pyramid adjacency lists	{\ displaystyle O ((V + E) \ log V) = O (E \ log V)}
Fibonacci's pyramid, adjacency lists	{\ displaystyle O (E + V \ log V)}

See also

• Minimum spanning tree (Prim's algorithm) online calculator