Lecture
Accurate knowledge of the number of operations performed by the algorithm does not play a significant role in the analysis of algorithms. Much more important is the growth rate of this number with an increase in the volume of input data. This rate is called the growth order of the algorithm. We are interested only in the general nature of the behavior of the algorithms, and not in the details of this behavior. When analyzing algorithms, we will rather be interested in the growth order class to which the algorithm belongs, than the exact number of operations of each type it performs (Table 2.1).
Fast growing features dominate slow growth functions. Therefore, if it was revealed that the growth order of the algorithm is the sum of two or several functions, then all functions are often rejected except those that grow the fastest. If, for example, it is established that the algorithm makes comparisons, then it is said that the growth order of the algorithm is equal.
Table 2.1 - Some classes of growth orders
|
Number of elements of the algorithm input |
||||||
|
1 |
0 (1) |
0 (1) |
0 (1) |
0 (1) |
0 (1) |
0 (2) |
|
10 |
3 |
10 |
33 |
100 |
1000 |
1024 |
|
20 |
4 |
20 |
86 |
400 |
8,000 |
1048576 |
|
50 |
6 |
50 |
282 |
2500 |
125,000 |
|
|
100 |
7 |
100 |
664 |
10,000 |
1,000,000 |
The rate of growth of the complexity of the algorithm plays an important role, and is determined by the senior, dominant member of the formula.
Although in the analysis of algorithms all functions are assigned to the same class, the growth order of which coincides to a constant factor, there are many similar classes. For example, the order of growth of a function depends on. The time efficiency of a large number of algorithms can be attributed to one of several main classes (Table 2.2).
Table 2.2 - a list of the main classes of algorithms, depending on the temporal efficiency
|
Class |
Title |
Comment |
|
one |
constant |
If you do not take into account the efficiency of algorithms at best, a very small number of algorithms fall into this class. Usually, as the size of the input data increases, the execution time of the algorithm increases. |
| log n |
logarithmic |
Typically, this dependence appears as a result of reducing the size of the problem to a constant value at each step of the algorithm iteration. In the logarithmic method, it is impossible to work with all input data (and even with some fixed part of them). In this case, the execution time of any algorithm will be at least linearly dependent on the size of the input data. |
| n |
linear |
This class includes algorithms that perform a scan of a list consisting of elements, for example, a search algorithm by sequential search. |
| n log n | n log n |
This class includes most decomposition algorithms, such as merge or quick sort algorithms. |
| n ^ 2 |
quadratic |
As a rule, such a dependence characterizes the efficiency of algorithms containing two built-in cycles. As typical examples, it suffices to call a simple sorting algorithm and a number of operations performed on matrices. |
| n ^ 3 |
cubic |
As a rule, such a dependence characterizes the efficiency of algorithms containing three built-in cycles. This class includes several rather complex algorithms of linear algebra. |
| 2 ^ n |
exponential |
This dependence is typical for algorithms that perform processing of all subsets of a certain set, which consists of elements. Often the term “exponential” is used in a broad sense and means very high orders of growth, i.e. including faster than exponential growth orders. |
| n! |
factorial |
This dependence is typical for algorithms that perform processing of all permutations of a certain set, which consists of elements. |
Considering the input data of a sufficiently large size to estimate only such a quantity as the order of growth of the algorithm operation time, we determine the asymptotic efficiency of the algorithms. This means that we are only interested in how the running time of the algorithm grows with the size of the input data to infinity. Usually, an algorithm that is efficient in the asymptotic sense will be productive for all input data, except for very small ones.
In order to be able to compare with each other these orders of growth and classify them, the following conventions were introduced: (pronounced “O large”),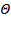 
("Large") and 
("Omega great").
Denote by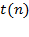 
algorithm execution time. Through 
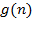let's denote Functions 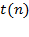and 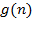can be any non-negative functions defined on the set of natural numbers.
Speaking loosely, designation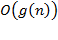 
Is the set of all functions, the order of growth of which for sufficiently large does not exceed (ie, less than or equal to) the value of some constant multiplied by the value of the function .
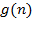Second designation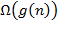 
, Is the set of all functions whose growth order for large enough is not less (that is, greater than or equal to) the value of some constant multiplied by the value of the function 
.
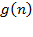Finally, the designation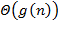 
Is the set of all functions whose growth order for sufficiently large is equal to the value of the constant multiplied by the value of the function .
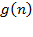The main indicator of the complexity of the algorithm is the time required to solve the problem and the amount of required memory.
Also, when analyzing the complexity for a class of tasks, a certain number is defined that characterizes a certain amount of data - the size of the input.
So, we can conclude that the complexity of the algorithm is a function of the size of the input.
The complexity of the algorithm may be different for the same input size, but different input data.
There are notions of complexity at worst, average or best. Usually, the complexity is estimated at worst.
In the worst case, the time complexity is a function of the size of the input, equal to the maximum number of operations performed during the operation of the algorithm in solving the problem of a given size.
In the worst case, capacitive complexity is a function of the size of the input, equal to the maximum number of memory cells that were addressed when solving problems of a given size.
The order of growth of complexity (or axiomatic complexity) describes the approximate behavior of the complexity function of an algorithm with a large input size. From this it follows that in assessing the time complexity there is no need to consider elementary operations, it suffices to consider the steps of the algorithm.
The step of the algorithm is a set of consecutive elementary operations whose execution time does not depend on the size of the input, that is, is bounded above by some constant.
Comments
To leave a comment
Algorithms
Terms: Algorithms