Span trees of minimum cost

Let G be (V, E) a connected graph in which each edge (v, w) is labeled with a number c (v, w), which is called the cost of the edge. The core tree of the graph G is the free tree containing all the vertices V of the graph G. The cost of the spanning tree is calculated as the sum of the values ​​of all edges included in this tree. In this section, we will look at methods for finding minimum spanning trees.

Minimum spanning tree of a connected graph
(edges of the minimum spanning tree separately highlighted in color)

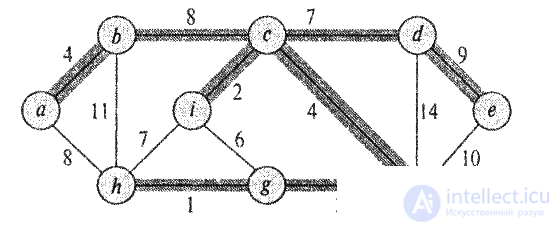
The given tree is not the only thing: removing the edge (b, c) and replacing it with the edge (a, h), we get another spanning tree with the same weight of 37.

In this chapter, we consider two algorithms for solving the problem of finding the minimum spanning tree — the Kruskal algorithm and the Prim algorithm. Each of them is easy to implement using ordinary binary pyramids, getting the operating time O (E * lgV). When using Fibonacci pyramids, the Prim algorithm can be accelerated to O (E + V * lgV), which is a very significant acceleration at | V | << | E |.

Both of these algorithms are greedy . At each step of the algorithm, we choose one of the possible options. A greedy strategy involves choosing the option that is best at the moment. In the general case, such a strategy does not guarantee a globally optimal solution of the problem; however, for the problem of finding the minimum spanning tree, one can prove that certain greedy strategies give us a spanning tree of minimal weight.