Lecture
Belarusian Republican Olympiad, 2002.
In some cities there is a subway consisting of N (1 <= N <= 1000) stations and M (0 <= M <= 500,000) lines connecting them. Each line provides travel between two stations in both directions. Between any pair of stations held no more than one line. The metro network is constructed in such a way that each station can be passed on to each (possibly through intermediate stations). We call this property the metro connectivity.
In connection with the invention of a fundamentally new type of transport, the metro became unprofitable, and it was decided to stop its work. At a meeting of the city hall, it was decided to close each year one station, but so that the metro connectivity is maintained each time. When closing any station, the lines leading from this station to others naturally also cease to function.
According to the information entered on the metro network, develop a procedure for closing stations, in which the metro will always remain connected. For example, let the subway look like the one shown in the picture.
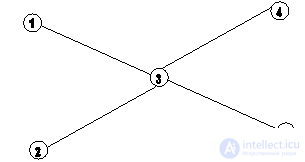
Then the station can be closed, for example, in the order 1,2,4,3,5. And the order 3,1,2,4,5 - does not fit, since after the closure of the 3rd metro station it will fall into four non-connected parts.
Input
The first line of the input file will contain the numbers N and M. The next M lines contain information about the lines. Each of these lines contains, separated by a space, the numbers Ai and Bi (Ai, Bi) - two stations that are connected by the i-th line.
Conclusion
The output file must consist of N lines. Each line must contain one number - the station number. Display stations need in order to close them.
Input Example Output Example 5 4 1 3 1 2 3 2 4 3 4 3 3 5 5
It is natural to imagine the metro stations with the tops of the graph, and the lines connecting them are the edges of the graph. Under the terms of the problem, the lengths of the lines do not matter, so we can set the weights of all edges to 1.
Now it is enough for us to find the spanning tree (we will look for the spanning tree using the Prim algorithm), and then bypass the original graph by searching in depth using only the edges included in the spanning tree.
Metro ()
1. Read the list of graph edges from the file, create a graph adjacency matrix.
2. Use the Prima algorithm to find the smallest skeleton tree
(comply with paragraphs 2.1-2.4):
3.1. Add all vertices to the queue, initialize the key value
infinity, and the array with the previous vertices -1.
3.2. Assign key value 0 to the starting vertex.
3.3. While there are vertices in the queue, repeat paragraphs. 3.3.1-3.3:
3.3.1. Find a vertex with a minimum key.
3.3.2. Remove found vertex from the queue.
3.3.3. Update key for all incident vertices that
are in line.
3.3.4. For all the incident vertices that are in the queue,
the vertex previous to them is the current vertex.
3. Build an adjacency matrix for the derived skeleton tree.
4. To go around all the vertices of the trunk tree inland, displaying the vertices on the screen.
Sample metro scheme.
The order of closure of stations: 3, 8, 9, 7, 6, 5, 4, 2, 1.
Comments
To leave a comment
Algorithms
Terms: Algorithms