Lecture
Any message with which we deal in information theory is a collection of information about a certain physical system. For example, a message about a normal or elevated reject rate, the chemical composition of the raw materials or the temperature in the furnace may be transmitted to the input of the automated control system of the production department. At the entrance of the air defense control system, a message can be transmitted that there are two targets in the air, flying at a certain height, at a certain speed. A message can be sent to the same input that a certain number of fighters are currently on alert at a particular aerodrome, or that the airfield is disabled by enemy fire, or that the first target was shot down, and the second one continues to fly with the changed course. Any of these messages describes the state of a physical system.
Obviously, if the state of the physical system were known in advance, there would be no point in transmitting the message. The message acquires meaning only when the state of the system is not known in advance, by chance.
Therefore, as an object about which information is transmitted, we will consider some physical system 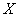 , which can randomly be in one or another state, i.e., a system that certainly has some degree of uncertainty. Obviously, information received about the system will, generally speaking, be more valuable and meaningful, the more the system’s uncertainty was before receiving this information (“a priori”). A natural question arises: what does “large” or “smaller” degree of uncertainty mean and how can it be measured?
, which can randomly be in one or another state, i.e., a system that certainly has some degree of uncertainty. Obviously, information received about the system will, generally speaking, be more valuable and meaningful, the more the system’s uncertainty was before receiving this information (“a priori”). A natural question arises: what does “large” or “smaller” degree of uncertainty mean and how can it be measured?
To answer this question, we can compare two systems, each of which has some uncertainty.
As the first system, we take a coin, which as a result of the throwing can end up in one of two states: 1) the coat of arms fell out and 2) the figure fell out. As a second, the dice, which has six possible states: 1, 2, 3, 4, 5, and 6. It is asked, which system’s uncertainty is greater? Obviously, the second, since it has more possible states, in each of which it can be with the same probability.
It may seem that the degree of uncertainty is determined by the number of possible system states. However, in general this is not the case. Consider, for example, a technical device that can be in two states: 1) normal and 2) failed. Suppose that prior to obtaining information (a priori), the probability of the correct operation of the device is 0.99, and the probability of failure is 0.01. Such a system has only a very small degree of uncertainty: you can almost guess that the device will work properly. When throwing a coin, there are also two possible states, but the degree of uncertainty is much greater. We see that the degree of uncertainty of a physical system is determined not only by the number of its possible states, but also by the probabilities of states.
Let us turn to the general case. Consider some system 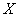 which can take a finite set of states:
which can take a finite set of states: 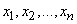 with probabilities
with probabilities 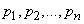 where
where
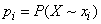 (18.2.1)
(18.2.1)
- the probability that the system 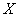 will take the state
will take the state 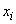 (symbol
(symbol 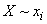 denotes the event: the system is in a state
denotes the event: the system is in a state 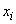 ). Obviously
). Obviously 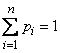 .
.
We write this data in the form of a table, where the upper line lists the possible states of the system, and the lower line shows the corresponding probabilities:
|
|
|
|
|
|
|
|
|
|
This writing tablet is similar to a series of distributions of a discontinuous random variable. 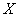 with possible values
with possible values 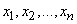 having probabilities
having probabilities 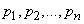 . And indeed, between the physical system
. And indeed, between the physical system 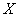 with a finite set of states and a discontinuous random variable much in common; in order to reduce the first to the second, it is sufficient to assign to each state some numerical value (say, the number of the state). We emphasize that to describe the degree of uncertainty of the system it does not matter at all what values
with a finite set of states and a discontinuous random variable much in common; in order to reduce the first to the second, it is sufficient to assign to each state some numerical value (say, the number of the state). We emphasize that to describe the degree of uncertainty of the system it does not matter at all what values 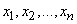 recorded in the top row of the table; only the number of these values and their probabilities are important.
recorded in the top row of the table; only the number of these values and their probabilities are important.
As a measure of a priori uncertainty of the system (or a discontinuous random variable 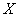 a) a special characteristic is used in information theory, called entropy. The concept of entropy is fundamental in information theory.
a) a special characteristic is used in information theory, called entropy. The concept of entropy is fundamental in information theory.
The entropy of a system is the sum of the products of probabilities of various states of the system by the logarithms of these probabilities, taken with the opposite sign:
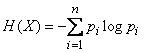 . (18.2.2)
. (18.2.2)
Entropy 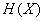 as we shall see, it has a number of properties that justify its choice as a characteristic of the degree of uncertainty. First, it vanishes when one of the states of the system is reliable, while others are impossible. Secondly, for a given number of states, it turns to a maximum when these states are equally probable, and with increasing number of states - it increases. Finally, and most importantly, it has the property of additivity, that is, when several independent systems are combined into one, their entropies are added.
as we shall see, it has a number of properties that justify its choice as a characteristic of the degree of uncertainty. First, it vanishes when one of the states of the system is reliable, while others are impossible. Secondly, for a given number of states, it turns to a maximum when these states are equally probable, and with increasing number of states - it increases. Finally, and most importantly, it has the property of additivity, that is, when several independent systems are combined into one, their entropies are added.
The logarithm in the formula (18.2.2) can be taken for any reason. 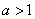 . The change of the base is equivalent to simply multiplying the entropy by a constant number, and the choice of the base is equivalent to choosing a certain unit of measurement of the entropy. If the number 10 is chosen for the base, then they speak of “decimal units” of entropy, if 2 - of “binary units”. In practice, it is most convenient to use logarithms at base 2 and measure entropy in binary units; This agrees well with the binary number system used in electronic digital computers.
. The change of the base is equivalent to simply multiplying the entropy by a constant number, and the choice of the base is equivalent to choosing a certain unit of measurement of the entropy. If the number 10 is chosen for the base, then they speak of “decimal units” of entropy, if 2 - of “binary units”. In practice, it is most convenient to use logarithms at base 2 and measure entropy in binary units; This agrees well with the binary number system used in electronic digital computers.
In the future, we will be everywhere, unless otherwise stated, under the symbol 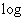 understand binary logarithm.
understand binary logarithm.
The appendix (Table 6) gives binary logarithms of integers from 1 to 100.
It is easy to verify that when choosing 2, the entropy of the simplest system is taken as the base of logarithms for the unit of entropy measurement 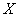 which has two equally possible states:
which has two equally possible states:
|
|
|
|
|
|
Indeed, by the formula (18.2.2) we have:
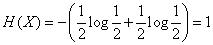 .
.
The entropy unit defined in this way is called a “binary unit” and is sometimes denoted by bit (from the English word “binary digit”). This is the entropy of one digit of a binary number, if it can be zero or one with the same probability.
Measuring in entropy of the system in binary units 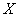 , which has
, which has 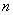 equiprobable states:
equiprobable states:
|
|
|
|
|
|
|
|
|
|
We have:
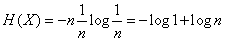
or
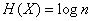 , (18.2.3)
, (18.2.3)
that is, the entropy of a system with equally possible states is equal to the logarithm of the number of states.
For example, for a system with eight states 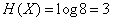 .
.
We prove that in the case when the state of the system is precisely known in advance, its entropy is zero. Indeed, in this case all probabilities 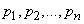 in the formula (18.2.2), they vanish, except for one - for example
in the formula (18.2.2), they vanish, except for one - for example 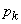 which is equal to one. Member
which is equal to one. Member 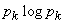 vanishes since
vanishes since 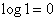 . The rest of the terms also vanish, since
. The rest of the terms also vanish, since
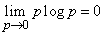 .
.
We prove that the entropy of a system with a finite set of states reaches a maximum when all states are equally probable. To do this, consider the entropy of the system (18.2.2) as a function of probabilities 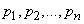 and find the conditional extremum of this function, provided:
and find the conditional extremum of this function, provided:
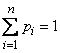 . (18.2.4)
. (18.2.4)
Using the method of uncertain Lagrange multipliers, we will look for the extremum of the function:
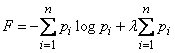 . (18.2.5)
. (18.2.5)
Differentiating (18.2.5) by 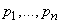 and equating the derivatives to zero, we obtain the system of equations:
and equating the derivatives to zero, we obtain the system of equations:
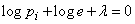
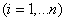
or
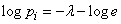
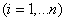 , (18.2.6)
, (18.2.6)
whence it is clear that the extremum (in this case, the maximum) is reached at equal values 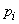 . From the condition (18.2.4) it can be seen that
. From the condition (18.2.4) it can be seen that
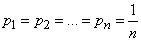 , (18.2.7)
, (18.2.7)
and the maximum entropy of the system is:
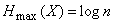 , (18.2.8)
, (18.2.8)
that is, the maximum entropy of a system with a finite number of states is equal to the logarithm of the number of states and is reached when all states are equally probable.
The calculation of entropy using the formula (18.2.2) can be somewhat simplified by introducing a special function into consideration:
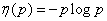 , (18.2.9)
, (18.2.9)
where the logarithm is taken over base 2.
The formula (18.2.2) takes the form:
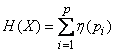 . (18.2.10)
. (18.2.10)
Function 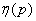 tabbed; the appendix (Table 7) gives its values for
tabbed; the appendix (Table 7) gives its values for  from 0 to 1 through 0.01.
from 0 to 1 through 0.01.
Example 1. Determine the entropy of a physical system consisting of two airplanes (fighter and bomber) participating in an air battle. As a result of the battle, the system may be in one of four possible states:
1) both aircraft are not shot down;
2) the fighter shot down, the bomber is not shot down;
3) the fighter is not shot down, the bomber shot down;
4) both aircraft shot down.
The probabilities of these states are respectively 0.2; 0.3; 0.4 and 0.1.
Decision. We write the conditions in the form of a table:
|
|
|
|
|
| 0.2 | 0.3 | 0.4 | 0.1 |
By the formula (18.2.10) we have:
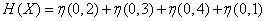 .
.
Using table 7 of the application, we find
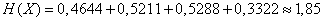 (two units).
(two units).
Example 2. Determine the entropy of a system whose state is described by a discontinuous random variable. 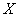 with a number of distribution
with a number of distribution
|
|
|
|
|
|
| 0.01 | 0.01 | 0.01 | 0.01 | 0.96 |
Decision.
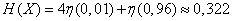 (two units).
(two units).
Example 3. Determine the maximum possible entropy of a system consisting of three elements, each of which can be in four possible states.
Decision. The total number of possible system states is 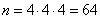 .The maximum possible entropy of the system is
.The maximum possible entropy of the system is 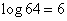 (two units).
(two units).
Example 4. Determine the maximum possible entropy of a message consisting of five letters, the total number of letters in the alphabet being 32.
Decision. The number of possible system states 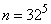 .The maximum possible entropy is equal
.The maximum possible entropy is equal 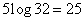 (dv. Units).
(dv. Units).
Formula (18.2.2) (or equivalent to it (18.2.10)) serves to directly calculate the entropy. However, when performing transformations, another form of entropy recording is often more convenient, namely, its representation in the form of a mathematical expectation:
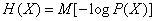 , (18.2.11)
, (18.2.11)
Where 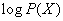 - the logarithm of the probability of any (random) state of the system, considered as a random variable.
- the logarithm of the probability of any (random) state of the system, considered as a random variable.
When the system 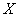 takes a state
takes a state 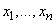 , the random variable
, the random variable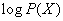 takes the values:
takes the values:
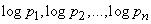 . (18.2.12)
. (18.2.12)
The mean value (mathematical expectation) of a random variable 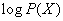 is, as is easily seen, the entropy of the system
is, as is easily seen, the entropy of the system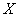 . To obtain it, the values (18.2.12) are averaged with “weights” equal to the corresponding probabilities
. To obtain it, the values (18.2.12) are averaged with “weights” equal to the corresponding probabilities 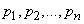 .
.
Formulas like (18.2.11), where entropy is represented as a mathematical expectation, allow us to simplify the transformations associated with entropy, reducing them to the application of well-known theorems about mathematical expectations.
Comments
To leave a comment
Algorithms
Terms: Algorithms