10 Network models. Algorithm for constructing a minimum spanning tree. Algorithm for determining the shortest path. Floyd's algorithm.

In practical life, there is a mass of mathematical programming problems that can be formulated and solved as network models (up to 70% are considered). Examples include:

- design of communication networks, including computer,

- designing a network of roads and finding the shortest routes,

- design of oil, gas, water, heating mains.

Basic definitions.

A network consists of a set of nodes connected by arcs (to match terminology with graph theory, we will call only oriented edges arcs, we will use an edge as a more general concept (and an edge, and an arc), the network node is equivalent to the top of the graph). The network is described by a pair of sets (N, A), where N is the set of nodes, A is the set of arcs.

N = {1, 2, 3, 4, 5},

A = {(1, 2), (1, 3), (2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 5) }.

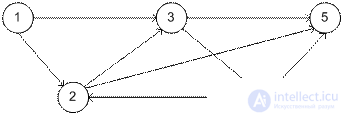
A specific stream type is associated with each type of network. In general, streams in networks are set by bandwidth.

A path is a sequence of edges connecting two nodes, regardless of the direction of flow in each edge. If the start and end nodes are the same, then the path is called a loop. For example, arcs (2, 3), (3, 4), (4, 2) form a cycle. A cycle can be oriented if all arcs are oriented in the same direction.

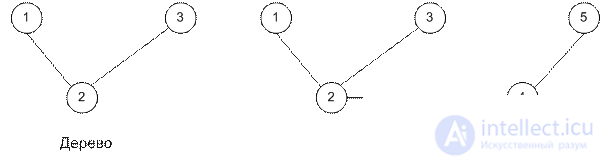
A connected network is a network in which any two nodes are connected in at least one way. The network in the picture is connected. A tree is a connected network that contains a subset of nodes in the source network and does not have loops. The spanning tree is a tree containing all the nodes in the network.

Algorithm for constructing a minimum spanning tree.

The algorithm for constructing a minimum spanning tree involves connecting all the nodes using the paths of the smallest length.

We describe this algorithm. Let N = {1, 2, ..., n} denote the set of network nodes and introduce the notation:

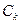- a set of network nodes connected by an algorithm after performing the k-th iteration of this algorithm.

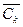- a set of network nodes that are not connected to the set nodes after the kth iteration of the algorithm has been completed.

k = 0. Stage 0. Assume C ₀ = Ø and 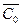= N.

k = 1. Stage 1.

Choose any node i from the set 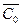and define C ₁ = {i}. Then 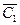= N - {i}. We assume k = 2.

Main stage k.

In the set 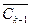choose the node j *, which is connected by the shortest arc to any node from the set C _{k -1} . The node j * joins the set C _{k -1} and is removed from the set 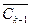. Thus, C _k = C _{k -1} + {j *}, 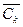= 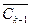- {j *}.

If many 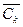empty, then the execution of the algorithm ends. Otherwise, we set k = k + 1 and repeat the last stage.

Example.

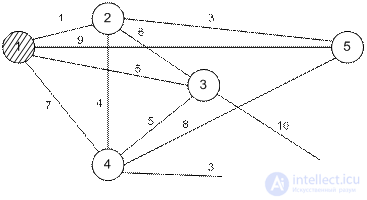
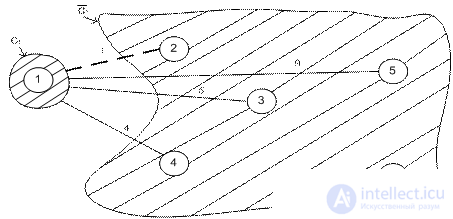
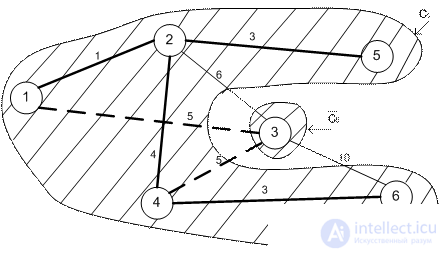
The television company is planning to connect five new areas to its cable network. The figure shows the structure of the planned network and the distance between the regions and the telecentre. It is necessary to plan the most economical cable network.

To start the execution of the algorithm, choose node 1 (or any other). Then

C ₁ = {1}, = {2, 3, 4, 5, 6}.

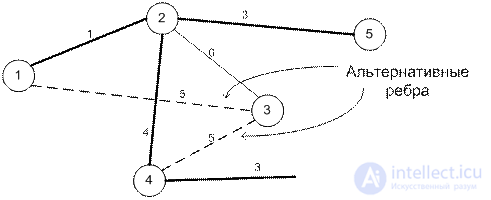
Consider successive iterations. The thin lines show the edges connecting the nodes belonging to the sets C _k and among which we look for an edge of minimal length. Found edge is shown by dashed line. Thick solid lines indicate the edges connecting the nodes of the set C _k (which were previously denoted by dashed lines).

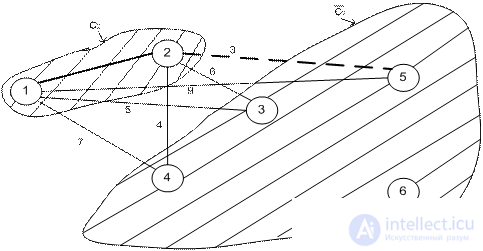
Iteration 1.

The edge (1, 2) has the lowest cost. therefore

j * = 2, C ₂ = {1, 2}, 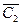= {3, 4, 5, 6}.

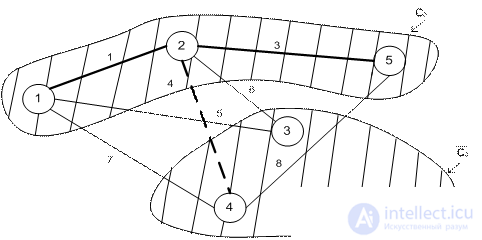
Iteration 2.

Iteration 3.

Iteration 4.

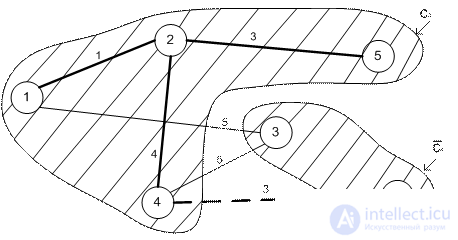
Iteration 5.

Iteration 6.

The solution was obtained at the 6th iteration. The minimum cable length for building a cable network is 1 + 3 + 4 + 3 + 5 = 16 km.

Algorithm for determining the shortest path.

1. Algorithm Dijkstra.

This algorithm is designed to find the shortest path between a given source node and any other network node.

In the process of executing this algorithm, when passing from node i to the next node j, a special procedure for marking edges is used. Let u _i denote the shortest distance from the source node 1 to the node i, and d _{ij the} edge length (i, j). Then for the node j we define the label [u _ij , i] as follows.

[u _j , i] = [u _i + d _ij , i], d _ij ≥0.

Node labels in Dijkstra's algorithm can be of two types: temporary and permanent. The timestamp can later be replaced by another timestamp, if a shorter path to this node is found. When it becomes obvious that there is no shorter path from the source node to this one, the status of the timestamp changes to a permanent one.

Computational algorithm scheme.

Step 0. The source node (node ​​1) is assigned a permanent label [0, -]. We assume i = 1.

Stage 1.

a) Calculate timestamps [u _i + d _ij , i] for all nodes j, which can be reached directly from node i and which do not have permanent marks. If node j already has a label [u _j , k] received from another node k, and if u _i + d _ij <u _j , then the label is replaced with [u _i + d _ij , i].

b) If all nodes have permanent labels, the calculation process ends. Otherwise, the [u _r , s] label is selected with the smallest distance u _r among all time marks (if there are several such tags, then the choice is arbitrary). We set i = r and repeat step i.

Example. A transport network is shown connecting five cities with specified distances. It is necessary to find the shortest distance from city 1 (node ​​1) to all other cities.

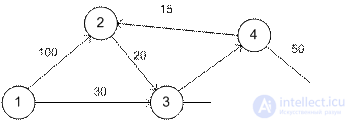
Step 0. Assign a constant label [0, -] to node 1.

Step 1. From node 1, you can reach nodes 2 and 3. We calculate the labels for these nodes.

Among nodes 2 and 3, node 3 has the smallest distance value (u ₃ = 30). Therefore, the status of the label is changed to permanent.

Stage 2. From node 3 (the last node with a permanent label) you can get to nodes 4 and 5. We get a list of tags.

The temporary status of the label [40, 3] of node 4 is replaced by a permanent (u ₄ = 40).

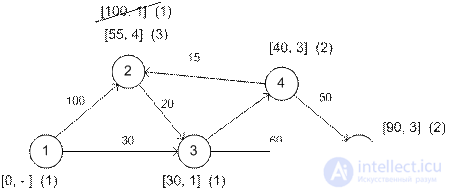
Stage 3. From node 4 you can reach nodes 2 and 5.

The timestamp [100, 1], obtained by node 2 in stage 2, was replaced by [55, 4]: that is, a shorter path to this node was found (through node 4). In the third stage, node 5 receives two labels with the same distance value u ₅ = 90.

Step 4. From node 2 you can only go to node 3, but it already has a permanent label that cannot be changed. Therefore, the list of labels is the same, but with a single change: the label of node 2 receives the status of a permanent. With a timestamp, only node 5 remains, but since no other can be reached from this node, the calculation process ends.

The algorithm allows to perform calculations only on the network diagram.

(...) = step

The shortest route between node 1 and any other node is determined starting from the destination node by passing them in the opposite direction along the labels. For example, to determine the shortest route between nodes 1 and 2, we obtain the following sequence of nodes:

(2) → [55, 4] → (4) [40, 3] → (3) → [30, 1] → (1).

Thus, we obtain the path 1 → 3 → 4 → 2 with a total length of 55 km.

An example . The most reliable route.

Mr. Umnick goes to work every day by car. He identified the shortest path from home to work. Unfortunately, the road is heavily patrolled by the traffic police, and Mr. Umnick is often stopped for speeding. Thus, the shortest path is not the fastest. Therefore, Mr. Umnik plans to develop a new route, which would be the highest probability not to be stopped by the police.

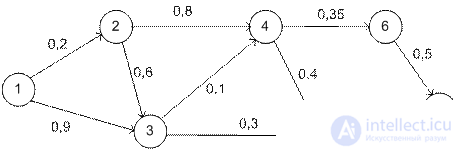
The diagram shows the probability of not being stopped by the traffic police for each segment. For example, the probability of not being stopped on the route 1 → 3 → 5 → 7 is 0.9 * 0.3 * 0.25 = 0.0675.

It is necessary to maximize the probability of not being stopped. Instead of probabilities, you can use logarithms of probabilities:

log p _1k = log p ₁ + log p ₂ + ... + log p _k .

Since log p _{1 k} ≤0, the problem is equivalent to minimization - log p _{1 k} .

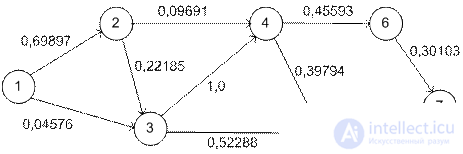
Using the TORA program, we find the shortest path 1 → 3 → 5 → 7 with the corresponding path length of 1.1707 (= - log p ₁₇ ), that is, the maximum probability of not being stopped is p ₁₇ = 0.0675.

Floyd's algorithm.

This algorithm is more general than the Dijkstra algorithm, since it finds the shortest path between any two nodes on the network.

In this algorithm, the network is represented by a square n × n matrix. Element (i, j) is equal to the distance d _ij from node i to node j, which is of course, if there is an arc (i, j), and is equal to infinity otherwise.

The basic idea of ​​the Floyd algorithm is as follows. Let there be three nodes i, j, and k and set the distances between them.

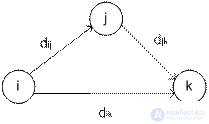
If the inequality d _ij + d _jk <d _ik holds, then it is advisable to replace the path i → k with i → j → k. Such a replacement (we will call it a triangular operator) is performed systematically during the execution of the Floyd algorithm.

Stages of the algorithm.

Step 0. Determine the initial distance matrix D _ij and the matrix of the sequence of nodes S ₀ . The diagonal elements of both matrices are marked with a “-” sign, indicating that these elements do not participate in the calculations. We assume k = 1.

Main stage k . Specifies the string k and the column k as the leading row and leading column. Consider the possibility of applying a triangular operator to all the elements d _{ij of the} matrix D _{k -1} . If inequality holds

d _ik + d _kj <d _ij (i ≠ k, j ≠ k, i ≠ j),

then do the following:

a) create the matrix D _k by replacing the element d _ij in the matrix D _{k -1} with the sum d _ik + d _kj ;

b) create the matrix S _k , changing the element S _ij by k in the matrix S _{k -1} . We set k = k + 1 and repeat step k.

Imagine the matrix D _k-1 as:

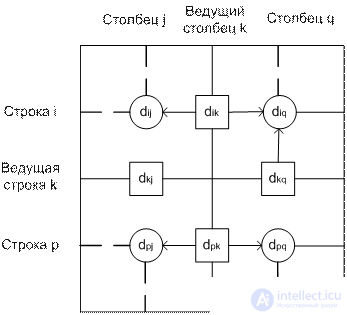
Line k and column k are leading. Line i is any number from 1 to k-1, line p is any number from k + 1 to n. Similarly with columns. The triangular operator is executed as follows. If the sum of the leading row and column elements (in squares) is less than the elements located at the intersection of the row and column (circles), then the distance (the element in the circle) is replaced by the sum of the distances represented by the leading elements.

After implementing the n steps of the algorithm, the shortest path ij is defined as follows.

1. The distance between nodes i and j is equal to the element d _ij in the matrix D.

2. Intermediate nodes are determined by the matrix S _n . Let S _ij = k,   then we have the path i → k → j. If S _ik = k and S _kj = j, then we assume that the whole path is defined, since All intermediate nodes found.