Search for maximum matching

Let a non-oriented graph G = (V, E) be given. A matching is a subset of edges M є E such that, for all vertices v ∈ V, M contains at most one edge incident to v.

Maximum matching is called maximum power matching, i.e. is the match M, that for any match M ': | M | > = | M '|.

We confine ourselves to the task of searching for maximal matching in bipartite graphs . We assume that the set of vertices can be divided into two subsets V = LUR, where L and R do not intersect, and all edges from E are between L and R. Further we assume that each vertex from V has at least one incident edge.

Using the Ford-Fulkerson method, one can find the maximum matching in the undirected bipartite graph G = (V, E) in a time polynomially dependent on | V | and | E |. For a given bichromatic graph G, we define the corresponding transport network G '= (V', E ') as follows. Take as a source of s and sink t new vertices that are not in V, and let V '= VU { s, t }. If the partition of the vertices in the graph G is given as V = LUR, the oriented edges of G will be the edges of E directed from L to R, and also | V | new ribs. To complete the construction, assign each edge E 'unit capacity.

Below is a bipartite graph and its corresponding transport network. The selected edges provide maximum flow and determine the maximum matching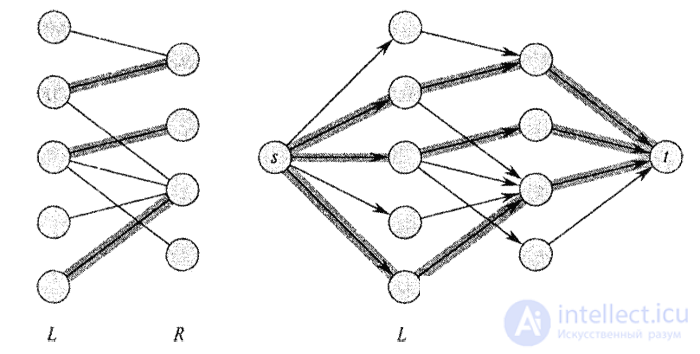

Formal description [up]

  Matching (G)
 1. Check whether the count is bichromatic.
 2. If the graph is bichromatic, then go to paragraph 2.1., Otherwise 
    display a message that the graph is non-trivial and complete the work.
    2.1.  Break the graph into 2 parts.
    2.2.  Create 2 vertices, associate a start with your vertices 
         from the first part of the graph, the final - with all vertices 
         from the second part of the graph.
    2.3.  Upgrade the resulting network by changing the bandwidth 
         in the opposite direction of the graph to negative values.
    2.4.  Find the maximum flow using the Ford-Fulkerson algorithm.
    2.5.  Count the edges between the two parts of the graph 
         with a stream equal to 1 pairing edges.
    2.6.  Count the number of edges in matching.

Evaluation of complexity [up]

Since any matching in a bipartite graph has a power of not more than min (L, R) = O (V), the maximum flux in G is O (V). Therefore, the maximum matching in a bichromatic graph can be found in time O (V * E ') = O (V * E) , since | E' | = o (E).

Example [up]

Consider a scheme for reducing a bichromatic graph to a network. The figure shows the original bipartite graph G.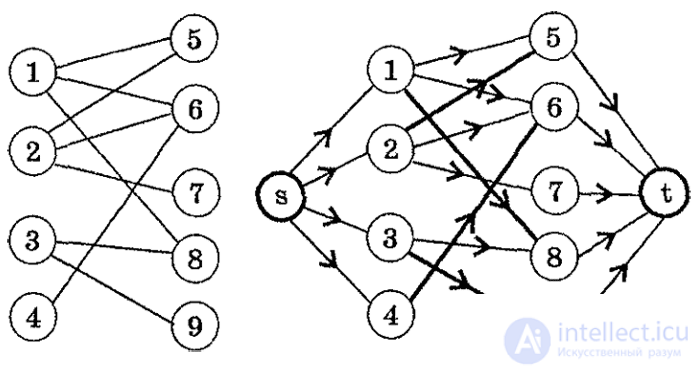

We construct a network S (G) with source s and drain t as follows:
* connect the source s by arcs with vertices from the set X;
* connect the vertices from the set Y by arcs with the drain t;
* the direction on the edges of the original graph will be from vertices from X to vertices from Y;
* bandwidth of all arcs C [i, j] = 1.
Find the maximum flow from s to t for the constructed network. He exists. Saturated arcs of the flow (they are highlighted by “bold” lines in the figure) correspond to the edges of the largest matching of the original graph. The largest matching found is not the only one.

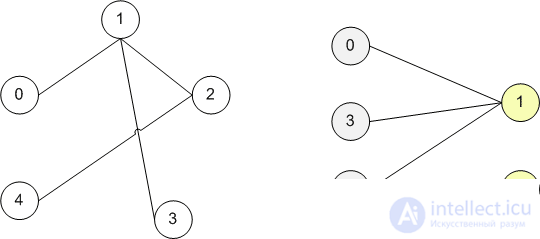
Find in the original graph (left) two parts and remember them. So we get a bichromatic graph.

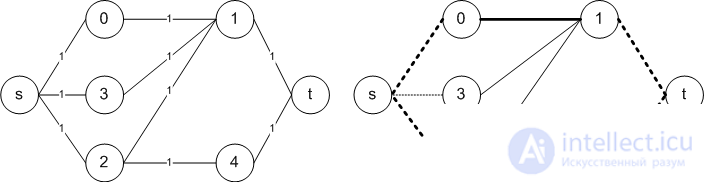
Add top-source and top-drain. Connect the source and drain with different parts of the graph.
For all edges, the throughput is 1. Find the maximum flow from the source to the drain.

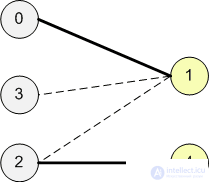
The edges of the original graph, through which the flow is equal to 1, will be the edges of the maximum matching. In this case, the maximum matching consists of 2 edges: (0; 1) and (2; 4).

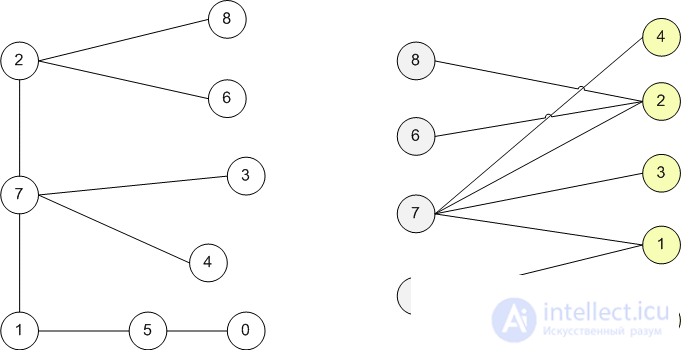
Find in the original graph (left) two parts and remember them. So we get a bichromatic graph.

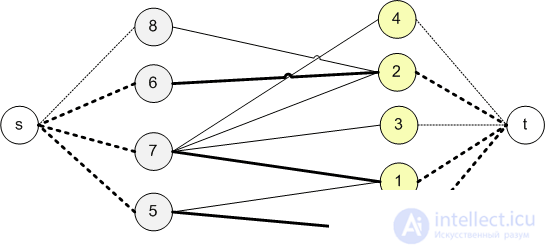
Add top-source and top-drain. Connect the source and drain with different parts of the graph.
For all edges we set the bandwidth equal to 1. Find the maximum flow from the source to the drain.

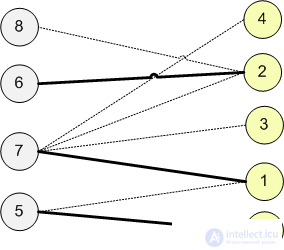
The edges of the original graph, through which the flow is equal to 1, will be the edges of the maximum matching. In this case, the maximum matching consists of 2 edges: (0; 1) and (2; 4).