Lecture
The interpolation search is based on the interpolation operation. Interpolation - finding intermediate values of a value over an existing discrete set of known values. Interpolation search only works with ordered arrays; it is similar to binary, in the sense that at each step a certain search area is computed, which, as the algorithm runs, narrows down. But unlike binary, interpolation search does not divide the sequence into two equal parts, but calculates the approximate location of the key (the desired element), focusing on the distance between the desired and the current value of the element. The idea of the algorithm resembles the search for a phone number in the usual directory that is well known to older generations: the list of caller names is ordered, so it’s not difficult to find the desired phone number, since, for example, we are looking for a subscriber with a last name starting with the letter “U”, then Further search will be reasonable to go to the end of the directory.
The formula that determines the interpolation search algorithm is as follows:
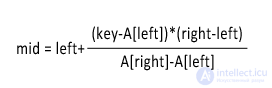
Here mid is the element number with which the key value is compared, key is the key (the desired element), A is an array of ordered elements, left and right are numbers of extreme elements of the search area. It is important to note that the division operation in the formula is strictly integer, that is, the fractional part, whatever it is, is discarded.
| one 2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 thirty 31 |
#include "stdafx.h"
#include using namespace std; const int N = 17; // interpolation search int InterpolSearch (int A [], int key) { int mid, left = 0, right = N-1; while (a [left] <= key && a [right]> = key) { mid = left + ((key-A [left]) * (right-left)) / (A [right] -A [left]); if (A [mid] else if (A [mid]> key) right = mid-1; else return mid; } if (A [left] == key) return left; else return -1; } // main function void main () { setlocale (LC_ALL, "Rus"); int i, key; int A [N] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59}; cout << "Search Item>"; cin >> key; // enter key cout << "Source array:"; for (i = 0; i if (InterpolSearch (A, key) == - 1) cout << "\ nItem is not found"; else cout << "\ nItem number:" << InterpolSearch (A, key) +1; system ("pause >> void"); } |
| one 2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 |
program InterpolationSearch;
uses crt; const N = 17; type Arr = array [1..N] of integer; var mid, left, right, key, i: integer; const A: Arr = (2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59); {interpolation search} function InterpolSearch (A: Arr; key: integer): integer; begin left: = 1; right: = N; while ((A [left] <= key) and (A [right]> = key)) do begin mid: = left + ((key-A [left]) * (right-left)) div (A [right] -A [left]); if (A [mid] else if (A [mid]> key) then right: = mid-1 else begin InterpolSearch: = mid; exit; end; end; if (A [left] = key) then InterpolSearch: = left else InterpolSearch: = - 1; end; {main program block} begin write ('search element>'); read (key); {key entry} write ('Source array:'); for i: = 1 to N do write (A [i], ''); {array output} writeln; if (InterpolSearch (A, key) = - 1) then write ('Element not found') else write ('Element number:', InterpolSearch (A, key)); end. |
Interpolation search in efficiency, as a rule, exceeds the binary one, on average requiring log (log (N)) operations. Thus, the time of his work is O (log (log (N))). But if, for example, the sequence increases exponentially, then the speed will increase to O (N), where N (as in the previous case) is the total number of items in the list. The algorithm shows the highest performance on a sequence whose elements are evenly distributed relative to each other.
Java:
Comments
To leave a comment
Algorithms
Terms: Algorithms