Bubble Sort

The most famous (and notorious) algorithm is bubble sort (bubble sort, bubble sort, or just bubble sort) ^[1] . Its popularity is explained by the interesting name and simplicity of the algorithm itself. However, in general this is one of the worst sorting algorithms.

Bubble sorting belongs to the class of exchange sorts, i.e. to the class of sorting by exchange. Its algorithm contains repeated comparisons (ie, multiple comparisons of the same elements) and, if necessary, the exchange of neighboring elements. Elements behave like air bubbles in water - each of them rises to its level. A simple form of the sorting algorithm is shown below:

  / * Bubble sort.  * /
 void bubble (char * items, int count)
 {
   register int a, b;
   register char t;

   for (a = 1; a <count; ++ a)
     for (b = count-1; b> = a; --b) {
       if (items [b-1]> items [b]) {
         / * exchange elements * /
         t = items [b-1];
         items [b-1] = items [b];
         items [b] = t;
       }
     }
 }

Here items is a pointer to the array of characters to be sorted, and count is the number of elements in the array. Bubble sorting is performed in two cycles. If the number of elements in the array is equal to count , the outer loop causes the count array to be scanned - 1 time. This ensures that the elements are placed in the correct order by the end of the execution of the function, even in the worst case. All comparisons and exchanges are performed in the inner loop. (A slightly improved version of the bubble sorting algorithm terminates if there was not a single exchange when viewing the array, but this is achieved by adding another comparison with each pass of the internal loop.)

With this version of the bubble sort algorithm, you can sort arrays of characters in ascending order. For example, the following short program sorts the string entered by the user:

  / * Program calling the bubble sort function * /

 #include <string.h>
 #include <stdio.h>
 #include <stdlib.h>

 void bubble (char * items, int count);

 int main (void)
 {
   char s [255];

   printf ("Enter the string:");
   gets (s);
   bubble (s, strlen (s));
   printf ("Sorted line:% s. \ n", s);

   return 0;
 }

In order to visually show how bubble sorting works, suppose that the source array contains dcab elements. The following shows the state of the array after each pass:

  Start dcab
 Adcb pass 1
 Pass 2 abdc
 Pass 3 abcd

When analyzing any sorting algorithm, it is useful to know how many comparisons and exchanges will be performed in the best, average and worst cases. Since the characteristics of the executed code depend on such factors as optimization made by the compiler, the differences between processors and implementation features, we will not try to get the exact values ​​of these parameters. Instead, focus on the overall efficiency of each algorithm.

In bubble sorting, the number of comparisons is always the same, since two for loops are repeated a specified number of times, regardless of whether the list was initially ordered or not. This means that the bubble sort algorithm always performs

( n ² - n ) / 2

comparisons, where n is the number of elements to be sorted. This formula is derived on the grounds that the outer loop is executed n - 1 times, and the inner loop is executed on average n / 2 times. The product of these quantities gives the previous expression.

Pay attention to the term n ² in the formula. Bubble sorting is said to be an algorithm of order n ² , since its execution time is proportional to the square of the number of sorted elements. It is necessary to recognize that an algorithm of order n ^{2 is} not effective with a large number of elements, since the execution time grows exponentially depending on the number of elements being sorted. In fig. 21.1 shows a graph of the growth of the sorting time with increasing the size of the array.

In the bubble sort algorithm, the number of exchanges is at best zero if the array is already sorted. However, on average and worst cases, the number of exchanges is also of the order of n ² .

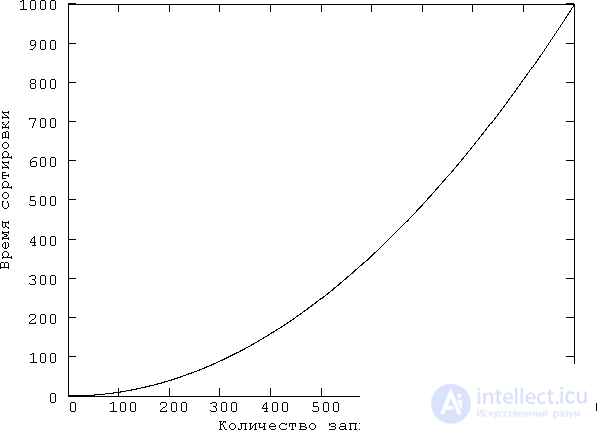
Fig. 21.1. Sorting time order n ² depending on the size of the array. (In fact, here the curve is drawn: y = n 2/1000, and not the curve y = n ² , the slope of which is 1000 times higher. In fact, it’s like drawing a curve y = n ² , choosing a smaller scale along the ordinate axis ( 1000 times). It is practically impossible to draw a curve y = n ² without stretching along the abscissa axis on which the n values ​​are laid. The fact is that with the selected interval of change n (from 0 to 1000) the curve y = n ² almost merges with axis of ordinates.)

Shaker sorting in C language

The bubble sorting algorithm can be slightly improved if you try to increase its speed. For example, bubble sorting has such a feature: unordered elements at the “big” end of the array (for example, “ a ” in the example of dñb ) occupy the correct positions in one pass, but unordered elements at the beginning of the array (for example, “ d ”) rise to their places So slow. This fact suggests a way to improve the algorithm. Instead of constantly looking at the array in one direction, you can alternate directions in successive passes. By this we will achieve that the elements, which are very remote from their positions, will quickly fall into place. This version of bubble sort is called shaker sort ^[2] , since the actions it performs with the array resemble shaking or shaking. The implementation of shaker sorting is shown below.

  / * Shaker sorting.  * /
 void shaker (char * items, int count)
 {
   register int a;
   int exchange;
   char t;

   do {
     exchange = 0;
     for (a = count-1; a> 0; --a) {
       if (items [a-1]> items [a]) {
         t = items [a-1];
         items [a-1] = items [a];
         items [a] = t;
         exchange = 1;
       }
     }

     for (a = 1; a <count; ++ a) {
       if (items [a-1]> items [a]) {
         t = items [a-1];
         items [a-1] = items [a];
         items [a] = t;
         exchange = 1;
       }
     }
   } while (exchange);  / * sort until exchanges * /
 }

Although shaker sorting is an improved option compared to bubble sorting, it still has a runtime of the order of n ² . This is explained by the fact that the number of comparisons has not changed, and the number of exchanges has decreased only by a relatively small constant. Shaker sorting is better than bubble sorting, but there are still much better sorting algorithms.

^[1] In fact, there are even two bubble sorting algorithms: bubble sorting and bubble sorting . However, the effectiveness of both is the same.

^[2] As well as sorting by shaking (cocktail shaker sort), sorting by shaking, sorting by shaking . However, this is a kind of bubble sort, in which alternative passes are performed in the opposite direction.