Lecture
Ford-Fulkerson algorithm - solves the problem of finding the maximum flow in the transport network.
The problem of the maximum flow for this network is as follows: to find the maximum possible rate of production (and consumption) of a substance, at which it can still be delivered from source to drain at given pipe carrying capacities.
Two concepts play a key role in the Ford-Fulkerson method: residual networks and complementary paths. Let the network and the flow in it be given. Then the residual network consists of those edges (also called residual), the flow of which can be increased. Note that the residual edge does not have to be an edge of the original network. Such "strange" ribs appear when there is a flow of matter in the opposite direction, because this flow can be reduced. We call the simple path from the source to the drain in the residual network a complementary path. It follows from the definition of the residual network that it is possible to send some more substance along all the edges of the complementary path without exceeding their carrying capacity. The value of the largest stream that can be sent along the complementary path is called the residual bandwidth of the path. Obviously, it is equal to the value of the minimum residual edge that enters this path.
During each iteration of the Ford-Fulkerson method, we find some increasing path p , and the flow f along each edge of a given path increases by the amount of residual capacity with f (p). The implementation of this method calculates the maximum flow in the graph G = (V, E) by updating the flow f [u, v] between each pair of vertices and and v connected by an edge. If the vertices u and v are not connected by an edge in any direction, it is implicitly assumed that f [u, v] = 0. It is assumed that the values of throughput are specified together with the graph and c (u, v) = 0 if ( u, v ) є E.
The residual capacity with f (u, v) is calculated by the formula c f (u, v) = c (u, v) - f (u, v).
Ford_Fulkerson (G, s, t) 1 for (for) each edge ( u, v ) є E [G] 2 do f [u, v] "-0 3 f [v, u] «- 0 4 while there is a path p from s to t in the residual network Gf
5 do cf (p) "- min { c f (u, v) : ( u, v ) belongs to p}
6 for (for) each edge ( u, v ) in p
7 do f [u, v] «- f [u] + c f (p)
8 f [v, u] "- -f [u, v]
Lines 1-3 initialize the flow f with value 0. In the while loop, in lines 4-8, a search is made repeatedly for the increasing path p in G f , and the flow f along the path p is increased by the residual capacity C f (p). When the increasing paths are no longer present, the flux f is maximum.
The execution time of the procedure Ford_Fulkerson depends on how exactly the search for the increasing path p is performed in line 4. If the search method is unsuccessful, the algorithm may not even end: the value of the flow will increase sequentially, but it will not necessarily converge to the maximum value of the flow.
Execution of lines 1-3 takes time in (E). The while loop on lines 4-8 executes no more than | f * | times, since the magnitude of the stream for each iteration increases by at least one unit. The search time of the path in the residual network is O (V + E ') = O (E), if you are using depth search or wide search. Each iteration of the while loop takes O (E) time, so as a result, the total execution time is O (E | f * |) , where f * is the maximum flow found by this algorithm.
The operation of the basic Ford-Fulkerson algorithm (successive iterations of the while loop). The left side of each figure shows the residual network G f with the selected increasing path p; The right side shows the new f stream, which is obtained by adding f p to f 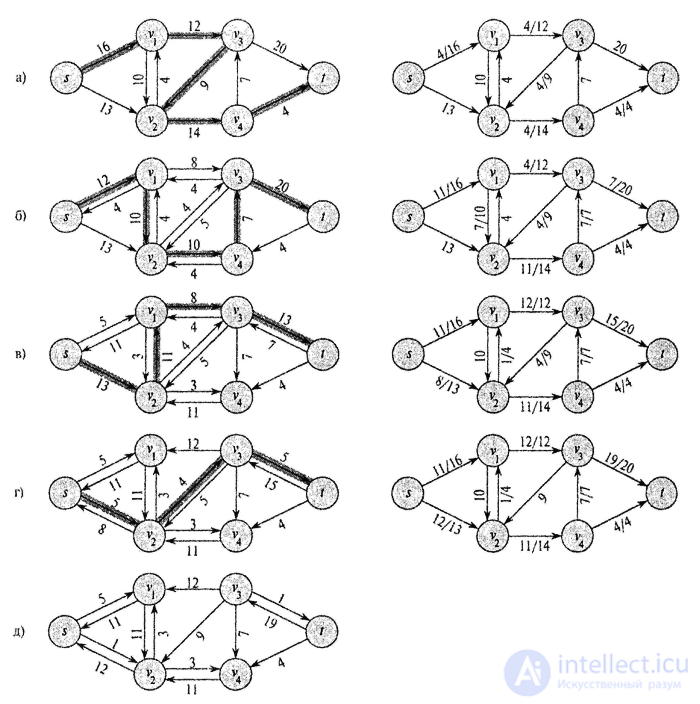
Comments
To leave a comment
Algorithms
Terms: Algorithms