Binary search

When the search for some element must be carried out in an ordered sequence in ascending or descending order, then we apply the binary (binary) search algorithm. The method uses the “divide and conquer” strategy, namely: a given sequence is divided into two equal parts and the search is performed in one of these parts, which then also divides in two, and so on until the presence of the desired element or its absence is detected. Using this operation, halving the search area each time, is only possible on the basis of the fact that the sequence elements are pre-ordered. Having found the middle element (it is not difficult to do this, knowing the number of elements in the array), and comparing its value with the desired one, we can confidently say where the required element is located relative to the middle element.

Further, we will assume that the elements of the array are arranged in ascending order, since there is no significant difference in how they are ordered: ascending or descending value. We also denote the boundaries of the search zone by left and right - the leftmost and rightmost elements, respectively.

The progress of the algorithm, divided into stages, is as follows:

1. the search area (in the first step, the entire array is divided into two), by defining its middle (mid) element;
2. the middle element is compared with the desired key, the result of this comparison will be one of three cases:
   • key <mid. The element at the middle (right ← mid-1) becomes the rightmost edge of the search area;
   • key> mid. The leftmost border of the search area becomes the next element after the middle (left ← mid + 1);
   • key = mid. The values ​​of the average and the required elements coincide, therefore the element is found, the algorithm is completed.
3. if there is no element left to check, the algorithm is completed, otherwise the transition to step 1 is performed.

The table below shows a specific integer array, and step-by-step execution of a binary search algorithm applied to its elements. To save space in the table, left, right and mid are replaced by a, b and c.

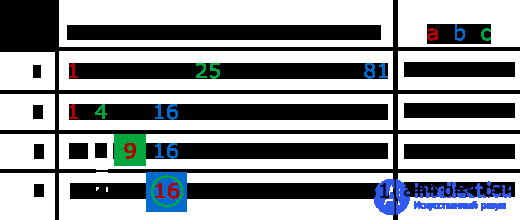
There is a sequence of integers arranged in ascending order, and the key is the number 16. Initially, the boundary elements are the elements with numbers 1 and 9, and the values ​​1 and 81. The number of the middle element is calculated, for which the formula is usually used (right + left) / 2, or left + (right-left) / 2 (further, the second formula will be used in the programs as the most resistant to overflows). After comparison, it turns out that the desired element is less than the average, and therefore the subsequent search is performed in the left part of the sequence. The algorithm continues to run in a similar way, until the desired element is found at step 4.

It should be noted that much less time is required here than if we used linear search, but unlike linear search, binary works only with arrays whose elements are ordered, which undoubtedly gives it negative specificity.

C ++ program code:

Pascal program code:

In the program, it would be possible to implement an array check for the presence of elements in it, but since it is filled, regardless of the user, by a strictly defined number of constant values, this is not necessary.

In the case when the first mid value coincides with the key, then it is considered that the algorithm was executed in its best time O (1). In average and worst case, the algorithm has a running time of O (log n ), which is much faster than a linear search that requires linear time.