Lecture
The algorithm of the Dutch scientist Edsger Dijkstra finds all the shortest paths from one initially defined vertex of the graph to all the others. With it, with all the necessary information, you can, for example, find out which sequence of roads is better to use to get from one city to each of many others, or to which countries it is more profitable to export oil and the like. The disadvantage of this method is the impossibility of processing graphs with negative weight edges, i.e. if, for example, some system provides routes that are unprofitable for your company, then you should use a method other than Dijkstra’s algorithm to work with it.
For the software implementation of the algorithm, we need two arrays: a logical visited - to store information about the visited vertices and a numerical distance in which the shortest paths will be entered. So, there is a graph G = (V, E). Each of the vertices in the set V is initially marked as not visited, that is, the elements of the visited array are set to false. Since the most profitable paths are only to be found, each element of the distance vector records a number that is obviously greater than any potential path (usually this number is called infinity, but the program uses, for example, the maximum value of a particular data type). The vertex s is selected as the starting point and the zero path is assigned to it: distance [s] = 0, since there is no edge from s to s (the method does not provide loops). Further, all adjacent vertices (which have an edge from s) are located (let t and u be such) and are investigated in turn, namely, the cost of the route from s is alternately calculated for each of them:
But it is quite probable that there are several paths to one or another vertex from s, so the price of the path to such a vertex in the distance array will have to be revised, then the highest (non-optimal) value is ignored, and the smallest is assigned to the vertex.
After processing the vertices adjacent to s, it is marked as visited: visited [s] = true, and that vertex becomes active, the path from s to which is minimal. Suppose the path from s to u is shorter than from s to t, therefore, the vertex u becomes active and its neighbors are investigated in the above manner, with the exception of the vertex s. Further, u is marked as passed: visited [u] = true, the vertex t becomes active, and the whole procedure is repeated for it. Dijkstra’s algorithm continues until all the vertices accessible from s are examined.
Now, on a specific graph, let us follow the operation of the algorithm, find all the shortest paths between the source and all the other vertices. The size (number of edges) of the graph shown below is 7 (| E | = 7), and the order (number of vertices) is 6 (| V | = 6). This is a weighted graph, each numerical value is assigned to each of its edges, so the route value is not necessarily determined by the number of edges lying between a pair of vertices.
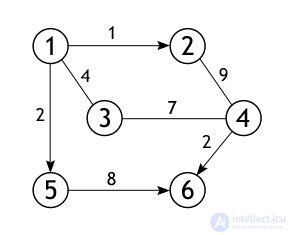
From all the vertices in the set V, we choose one, the one from which it is necessary to find the shortest paths to the other available vertices. Let vertex 1 be such. The length of the path to all vertices except the first is initially equal to infinity, and to it is 0, since the graph has no loops.
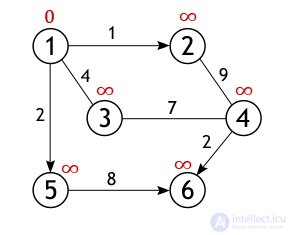
Vertex 1 has exactly 3 neighbors (vertices 2, 3, 5), and to calculate the length of the path to them, add the weight of the arcs lying between the vertices: 1 and 2, 1 and 3, 1 and 5 with the value of the first vertex (with zero) :
As already noted, the resulting values are assigned to the vertices, only if they are “better” (less) than those that appear at the moment. And since each of the three numbers is less than infinity, they become new values that determine the length of the path from vertex 1 to vertices 2, 3, and 5.
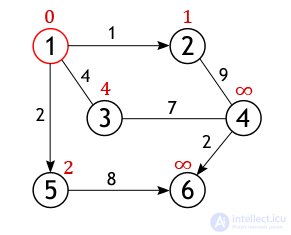
Further, the active vertex is marked as visited, the status of “active” (red circle) goes to one of its neighbors, namely, to peak 2, since it is closest to the previously active peak.
At vertex 2 there is only one not considered neighbor (vertex 1 is marked as visited), the distance to which is 9, but we need to calculate the length of the path from the source vertex, for which we add the value assigned to vertex 2 with the weight of the arc from it to vertex 4 :
The condition of “brevity” (10 <∞) is fulfilled, therefore, vertex 4 receives a new value of the path length.
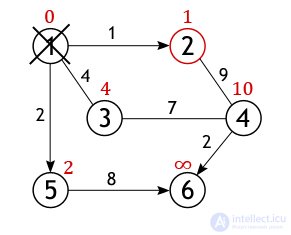
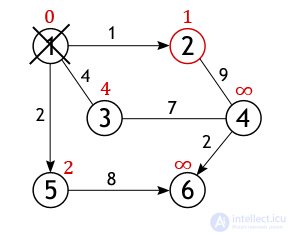
Vertex 2 ceases to be active, as well as vertex 1 is removed from the list of not visited. Now the neighbors of vertex 5 are examined in the same way, and the distance to them is calculated.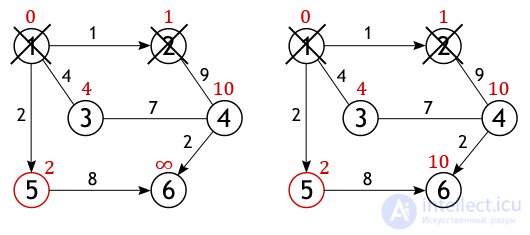 
When it comes to inspecting the neighbors of vertex 3, then it is important not to be mistaken, since vertex 4 has already been investigated and the distance of one of the possible paths from the source to it has been calculated. If we move to it through vertex 3, then the path will be 4 + 7 = 11, and 11> 10, so the new value is ignored, the old one remains.
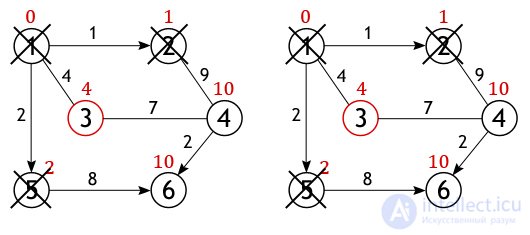The situation is similar with vertex 6. The value of the closest path to it from vertex 1 is 10, and it turns out only if you go through vertex 5. 
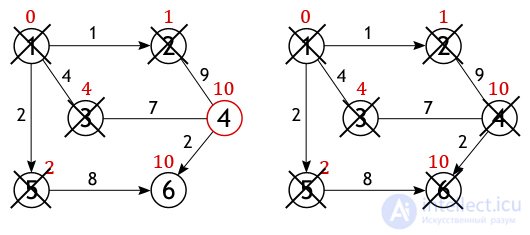When all the vertices of the graph, or all those that are accessible from the source, will be marked as visited, then the work of the Dijkstra algorithm will end, and all the paths found will be shortest. So, for example, a list of the most optimal distances lying between vertex 1 and all other vertices of the graph under consideration will look like:
1 → 1 = 0
1 → 2 = 1
1 → 3 = 4
1 → 4 = 10
1 → 5 = 2
1 → 6 = 10
In the program that finds the nearest path between the vertices using the Dijkstra method, the graph will be represented as a non-binary adjacency matrix. Instead of units, the weights of the edges will be set in it, the function of the zeros will remain the same: to show between which vertices there are no edges or they are, but negatively directed.
|
one |
#include "stdafx.h" |
|
one |
program DijkstraAlgorithm; |
Comments
To leave a comment
Algorithms
Terms: Algorithms