Sort Inserts

Insertion sorting is a simple sorting algorithm, mainly used in training programming. The positive side of the method is simplicity of implementation, as well as its effectiveness on partially ordered sequences, and / or consisting of a small number of elements. However, the high computational complexity does not allow recommending an algorithm for widespread use.

Consider the sorting algorithm inserts on the example of a deck of playing cards. The process of ordering them in ascending order (in a deck of cards arranged in a random order) will be as follows. Pay attention to the second card, if its value is less than the first, then we swap these cards, otherwise the cards retain their positions, and the algorithm proceeds to step 2. At the 2nd step, we look at the third card, here four cases of the relationship between card values ​​are possible :

1. the first and second cards are smaller than the third;
2. the first and second cards are larger than the third;
3. the first card is inferior to the value of the third, and the second one exceeds it;
4. the first card exceeds the value of the third card, and the second one is inferior to it.

In the first case, no permutations occur. In the second - the second card is shifted to the third, the first to the second, and the third card takes the position of the first. In the penultimate case, the first card remains in place, while the second and third cards change places. Finally, the last case requires casting only the first and third cards. All subsequent steps are completely similar to those described above.

Consider the example of the numerical sequence of the process of sorting the method of inserts. The cell highlighted in dark gray is an active element at this step, it also corresponds to the i-th number. Light gray cells are those elements whose values ​​are compared with the i-th element. All that is painted white is the part of the sequence that is not affected by the step.

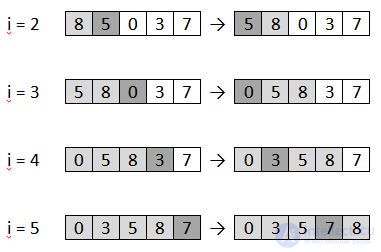
The animated image below shows another example of how the inserts sorting algorithm works. Here, as in the previous example, the sequence is sorted in ascending order.

Thus, it turns out that at each stage of the algorithm execution, some part of the array is sorted, the size of which increases in increments, and at the end the entire array is sorted.

C ++ program code:

Pascal program code:

Both programs sort the array in ascending order. In their main part, three operations are performed: determining the number of elements in the array, entering these elements and calling the subroutine. A subroutine consists of a sorting algorithm and a loop that outputs the resulting ordered sequence. The algorithm includes the structure of nested loops, which is classical for many sorting algorithms. The number of iterations of the outer loop does not exceed n-1, where n is the number of elements in the array; the internal loop, starting with step i + 1, ends its execution at j = 0 (the value of the counter variable j decreases with each step by 1). The key and temp variables in the i-th step are assigned values ​​depending on the step and the values ​​of the element of the mas array in this step. The temp variable stores the value of the element of the mas [i + 1] array; it is compared in the internal loop with the values ​​of other elements. Key remembers the index of the element that last was more than temp, and upon completion of the inner loop, the value of the variable temp is assigned.