Lecture
When they say "number to share," they mean that it is to share without a trace. So A is divisible by B, only if the remainder of their division is zero. The concept of the greatest common divisor (GCD) is based on this property. The GCD of two numbers is the largest of all their common divisors.
One of the simplest algorithms for finding the greatest common divisor is the Euclidean Algorithm. It is named after the famous ancient Greek mathematician, the author of the first theoretical treatises in mathematics that have come down to us - Euclid of Alexandria. There are two ways to implement the algorithm: the method of division and the method of subtraction. Consider separately each of them.
Finding the GCD of two integers is a little easier using the subtract operation. To do this, you need to follow this condition: if A = B, then the GCD is found and it is equal to one of the numbers, otherwise you need to replace the larger of the two numbers with its difference and the smaller one.
The block diagram of the Euclidean algorithm by subtraction:
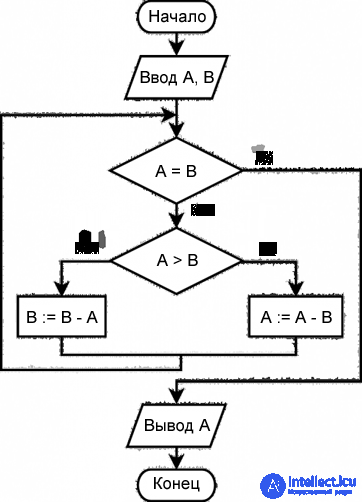
Operating with this block diagram — making up the program code for it, it is quite expedient to include in it a loop operator with a nested conditional branch operator having two branches.
|
one
2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 |
#include "stdafx.h"
#include using namespace std; // Euclidean algorithm. Subtraction int NOD (int A, int B) { while (a! = b) if (A> B) A- = B; else B- = A; return A; } // main function void main () { setlocale (LC_ALL, "Rus"); int A, B; cout << "A>"; cin >> A; cout << "B>"; cin >> B; cout << "NOD (" << A << "," << B << ") =" << NOD (A, B); system ("pause >> void"); } |
|
one
2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 |
program AlgEvklid;
uses crt; var A, B: integer; {Euclidean algorithm. Subtraction} function NOD (A, B: integer): integer; begin while a <> b do if A> B then A: = AB else B: = BA; NOD: = A; end; {main program block} begin write ('A>'); read (A); write ('b>'); read (B); write ('GCD (', A, ',', B, ') =', NOD (A, B)); readkey; end. |
The second method differs from the first one in that in the main part of the program the subtraction operation is replaced by a division operation, more precisely, by taking the remainder of dividing a large number by a smaller number. This method is preferable to the previous one, since it is in most cases more efficient, requires less time. With specific examples, we will demonstrate the work of each type of algorithm implementation. To begin with, based on the operation of taking the remainder of the division. We have two numbers: 112 and 32. The first is larger than the second — we replace it with the remainder of dividing 112 by 32. The new pair of numbers includes 16 and 32. The second is larger, so we also replace it with the remainder of dividing 32 by 16, i.e. zero. As a result, we obtain a gcd = 16. Tabularly it looks like this:
|
Initial data |
112 |
32 |
|
Step 1 |
sixteen |
32 |
|
Step 2 |
sixteen |
0 |
And now with the same numbers we compose a table for the subtraction algorithm.
|
Initial data |
112 |
32 |
|
Step 1 |
80 |
32 |
|
Step 2 |
48 |
32 |
|
Step 3 |
sixteen |
32 |
|
Step 4 |
sixteen |
0 |
The given example demonstrated how, in the particular case, preferring division (taking the remainder of division) to subtraction, you can win in speed. The advantage of division becomes visible most clearly after the following reasoning. Suppose that A is less than B, and since the GCD of two integers is less than or equal to the smallest of them, then it is less than or equal to A; therefore, it will be optimal even at the first operation to replace B with a number less than or equal to A. Further, it is known that in one case a larger number is replaced by its difference and a smaller number, and in the other by the remainder of division. When dividing B by A (more by less), the remainder cannot exceed the number in the denominator (i.e., A), therefore taking the remainder of the division guarantees an optimal outcome. But the same cannot be said with regard to the operation of subtraction, since it is not necessary that immediately after the first subtraction, B becomes less than or equal to A. For example, let A be equal to 150, and B - 1100. So, using subtraction, we in the first step, we get B equal to 950, while the division method will give 50.
The block diagram of the Euclidean algorithm by dividing:
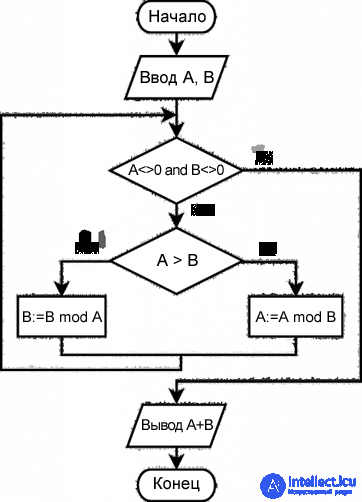
Except for the loop exit condition and operations in expressions, this block diagram is similar to the previous one. It is enough that the condition under which the body of the cycle will be fulfilled as long as both variables have nonzero values, since when the condition ceases to be true, it follows from this that one of the present values is the sought greatest common divisor. And then, there is no way to allow the next iteration, in which an attempt will be made to divide by zero.
|
one
2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 |
#include "stdafx.h"
#include using namespace std; // Euclidean algorithm. Division int NOD (int A, int B) { while (A! = 0 && B! = 0) if (A> B) A% = B; else B% = A; return A + B; } // main function void main () { setlocale (LC_ALL, "Rus"); int A, B; cout << "A>"; cin >> A; cout << "B>"; cin >> B; cout << "NOD (" << A << "," << B << ") =" << NOD (A, B); system ("pause >> void"); } |
|
one
2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 |
program AlgEvklid;
uses crt; var A, B: integer; {Euclidean algorithm. Division} function NOD (a, B: integer): integer; begin while (a <> 0) and (b <> 0) do If A> B then A: = A mod B else B: = B mod A; NOD: = A + B end; {main program block} begin write ('A>'); read (A); write ('b>'); read (B); write ('GCD (', A, ',', B, ') =', NOD (A, B)); readkey; end. |
Comments
To leave a comment
Algorithms
Terms: Algorithms