Lecture
In practice, it is often necessary to determine the entropy for a complex system obtained by combining two or more simple systems.
Under the union of the two systems 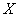 and
and 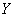 with possible states
with possible states 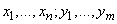 complex system is understood
complex system is understood 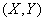 whose state
whose state 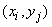 represent all possible combinations of states
represent all possible combinations of states 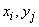 systems
systems 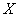 and
and 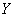 .
.
Obviously, the number of possible system states 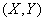 equally
equally 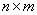 . Denote
. Denote 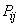 probability that the system
probability that the system 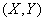 will be able to
will be able to 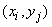 :
:
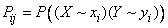 . (18.3.1)
. (18.3.1)
Probabilities 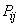 conveniently arranged in a table (matrix)
conveniently arranged in a table (matrix)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Find the entropy of a complex system. By definition, it is equal to the sum of the products of the probabilities of all its possible states to their logarithms with the opposite sign:
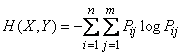 (18.3.2)
(18.3.2)
or, in other designations:
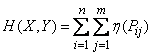 . (18.3.2 ')
. (18.3.2 ')
The entropy of a complex system, like the entropy simple, can also be written in the form of a mathematical expectation:
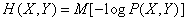 , (18.3.3)
, (18.3.3)
Where 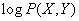 - the logarithm of the probability of the state of the system, considered as a random variable (state function).
- the logarithm of the probability of the state of the system, considered as a random variable (state function).
Suppose the systems 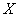 and
and 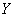 are independent, that is, they take their states independently of one another, and we calculate under this assumption the entropy of a complex system. By the probability multiplication theorem for independent events
are independent, that is, they take their states independently of one another, and we calculate under this assumption the entropy of a complex system. By the probability multiplication theorem for independent events
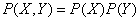 ,
,
from where
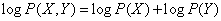 .
.
Substituting in (18.3.3), we get
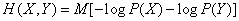 ,
,
or
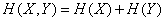 , (18.3.4)
, (18.3.4)
that is, when combining independent systems, their entropies are added.
The proven position is called the entropy addition theorem.
The entropy addition theorem can be easily generalized to an arbitrary number of independent systems:
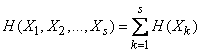 . (18.3.5)
. (18.3.5)
If the systems being combined are dependent, simple addition of entropy is no longer applicable. In this case, the entropy of a complex system is less than the sum of the entropies of its constituent parts. To find the entropy of a system composed of dependent elements, you need to introduce a new concept of conditional entropy.
Comments
To leave a comment
Algorithms
Terms: Algorithms