Lecture
In 1959, the American scientist Donald Schell published a sorting algorithm, which subsequently received his name - "Shell Sort." This algorithm can be considered both as a generalization of bubble sorting and sorting by inserts.
The idea of the method is to compare the elements of a sequence divided into groups that are at some distance from each other. Initially, this distance is equal to d or N / 2, where N is the total number of elements. In the first step, each group includes two elements spaced N / 2; they are compared with each other, and, if necessary, change places. At subsequent steps, verification and exchange also occur, but the distance d is reduced by d / 2, and the number of groups, respectively, decreases. Gradually, the distance between the elements decreases, and d = 1 passes through the array for the last time.
Further, by the example of a sequence of integers, the process of sorting an array using the Shell method is shown. For convenience and clarity, the elements of one group are highlighted in the same color.
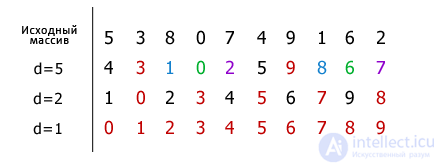
The first value corresponding to the distance d is 10/2 = 5. At each step, it is halved. The elements belonging to one group are compared and if the value of any element standing to the left of that with which it is compared turns out to be more (sorting ascending), then they switch places. Thus, the elements by intragroup permutations gradually become their positions, and at the last step (d = 1), the sorting is reduced to passing through one group, which includes all N elements of the array. At the same time, the number of exchanges required is quite small.
|
one
2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 thirty 31 32 33 34 35 36 37 38 |
#include "stdafx.h"
#include using namespace std; int i, j, n, d, count; void Shell (int A [], int n) // Shell sort { d = n; d = d / 2; while (d> 0) { for (i = 0; i { j = i; while (j> = 0 && A [j]> A [j + d]) { count = A [j]; A [j] = A [j + d]; A [j + d] = count; j--; } } d = d / 2; } for (i = 0; i } // main function void main () { setlocale (LC_ALL, "Rus"); cout << "Array size>"; cin >> n; int * A = new int [n]; // declare a dynamic array for (i = 0; i {cout << i + 1 << "element>"; cin >> A [i]; } cout << "\ nThe resulting array:"; Shell (A, n); delete [] A; // freeing memory system ("pause >> void"); } |
|
one
2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 thirty 31 32 33 34 35 |
program ShellSorting;
uses crt; type massiv = array [1..100] of integer; var i, j, n, d, count: integer; A: massiv; procedure Shell (A: massiv; n: integer); {shell sort} begin d: = n; d: = d div 2; while (d> 0) do begin for i: = 1 to nd do begin j: = i; while ((j> 0) and (A [j]> A [j + d])) do begin count: = A [j]; A [j]: = A [j + d]; A [j + d]: = count; j: = j-1; end; end; d: = d div 2; end; writeln; for i: = 1 to n do write ('', A [i]); {array output} end; {main program block} begin write ('array size>'); read (n); for i: = 1 to n do {array input} begin write (i, 'element>'); readln (a [i]); end; write ('Resulting array:'); Shell (A, n); end. |
Shell sorting is inferior in quick sorting efficiency, but wins out sorting by inserts. You can compare the speed of these three algorithms using the following table.
|
Sort Inserts |
Shell sort |
Quick sort |
|
|
Worst case |
O ( n 2 ) |
O ( n 2 ) |
O ( n 2 ) |
|
Best case |
O ( n ) |
O ( n log n ) |
O ( n log n ) |
|
Average case |
O ( n 2 ) |
Depends on the distance between the elements. |
O ( n log n ) |
Comments
To leave a comment
Algorithms
Terms: Algorithms