Sundaram Sieve - an algorithm for finding all primes in a given range. It was developed in 1934 by the now unknown student from India S.P. Sundaram.
The principle of operation of the Sundaram algorithm is reduced, as in its famous predecessor, to the sequential elimination of all unnecessary numbers. But it has one small feature: the result of the algorithm will be a sequence of primes from the range from 2 to twice the value of the boundary number. Suppose you need to get all the primes to some N, then the output will be all the primes from 2 to 2N + 1.
The Sundaram sieve excludes numbers of the form 2ij + i + j from the series of natural numbers not exceeding N. The result of this expression, for any values of variables included in it, does not exceed N (2ij + i + j≤N). Observing this condition, as well as the fact that i is always less than or equal to j, the variables i and j run through all natural values from the sets:
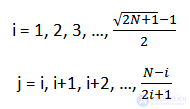
After eliminating all unnecessary numbers, it is necessary to double each remaining number and add one (2i + 1). The final set will contain the numbers: 2, 3, ..., 2N + 1.
C ++ program code:
|
one
2
3
four
five
6
7
eight
9
ten
eleven
12
13
14
15
sixteen
17
18
nineteen
20
21
22
23
24
25
26
27
28
29
thirty
31
32
33
|
#include "stdafx.h"
#include
using namespace std;
// Sieve Sundaram
void Sundaram (bool A [], int N)
{
int i, j;
for (i = 1; i <= N; i ++) A [i] = true;
i = 1; j = 1;
while ((2 * i * j + i + j) <= N)
{
while (j <= (Ni) / (2 * i + 1))
{
A [2 * i * j + i + j] = false;
j ++;
}
i ++;
j = i;
}
for (i = 1; i <= N; i ++)
if (A [i]) cout << 2 * i + 1 << "";
}
// main function
void main ()
{
setlocale (LC_ALL, "Rus");
int N, i, j;
bool A [1000];
cout << "N>"; cin >> N;
cout << "Prime numbers: 2";
Sundaram (A, N);
system ("pause >> void");
}
|
Pascal program code:
|
one
2
3
four
five
6
7
eight
9
ten
eleven
12
13
14
15
sixteen
17
18
nineteen
20
21
22
23
24
25
26
27
28
29
thirty
31
32
|
program SieveOfSundaram;
uses crt;
type arr = array [1..1000] of boolean;
var
N: integer;
A: arr;
{Sieve Sundaram}
procedure Sundaram (A: arr; N: integer);
var i, j: integer;
begin
for i: = 1 to N do A [i]: = true;
i: = 1; j: = 1;
while (2 * i * j + i + j) <= n do
begin
while j <= (Ni) / (2 * i + 1) do
begin
A [2 * i * j + i + j]: = false;
j: = j + 1;
end;
i: = i + 1;
j: = i;
end;
write (2, '');
for i: = 1 to n do
if A [i] then write (2 * i + 1, '');
end;
{main program block}
begin
write ('N>'); read (n);
writeln ('Prime numbers:');
Sundaram (A, N);
end.
|
See also
Comments
To leave a comment
Algorithms
Terms: Algorithms