Lecture
Существует три способа преобразования, т. е. изменения формы, простых суждений: обращение, превращение и противопоставление предикату.
Обращение ( конверсия ) – это преобразование простого суждения, при котором субъект и предикат меняются местами. Например, суждение: « Все акулы являются рыбами », – преобразуется путём обращения в суждение: « Некоторые рыбы являются акулами ». Здесь может возникнуть вопрос, почему исходное суждение начинается с квантора « все », а новое – с квантора « некоторые »? Этот вопрос, на первый взгляд, кажется странным, ведь нельзя же сказать: « Все рыбы являются акулами », – следовательно, единственное, что остаётся, это: « Некоторые рыбы являются акулами ». Однако в данном случае, мы обратились к содержанию суждения и по смыслу поменяли квантор « все » на квантор « некоторые »; а логика, как уже говорилось, отвлекается от содержания мышления и занимается только его формой. Поэтому обращение суждения: « Все акулы являются рыбами », – можно выполнить формально, не обращаясь к его содержанию (смыслу). Для этого установим распределённость терминов в этом суждении с помощью круговой схемы. Термины суждения, т. е. субъект « акулы » и предикат « рыбы », находятся в данном случае в отношении подчинения (рис. 27):
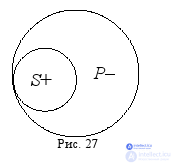
На круговой схеме видно, что субъект распределён (полный круг), а предикат нераспределён (неполный круг). Вспомнив, что термин распределён, когда речь идёт обо всех входящих в него предметах, и нераспределён, когда – не обо всех, мы автоматически мысленно ставим перед термином « акулы » квантор « все », а перед термином « рыбы » квантор « некоторые ». Делая обращение указанного суждения, т. е. меняя местами его субъект и предикат и начиная новое суждение с термина « рыбы », мы опять же автоматически снабжаем его квантором « некоторые », не задумываясь о содержании исходного и нового суждений, и получаем безошибочный вариант: « Некоторые рыбы являются акулами ». Возможно, всё это покажется чрезмерным усложнением элементарной операции, однако, как увидим далее, в иных случаях преобразование суждений сделать непросто без использования распределённости терминов и круговых схем.
Обратим внимание на то, что в рассмотренном выше примере исходное суждение было вида A , а новое – вида I , т. е. операция обращения привела к смене вида простого суждения. При этом, конечно же, поменялась его форма, но не поменялось содержание, ведь в суждениях: « Все акулы являются рыбами » и « Некоторые рыбы являются акулами », – речь идёт об одном и том же. In tab. 5 представлены все случаи обращения в зависимости от вида простого суждения и характера отношений между его субъектом и предикатом:
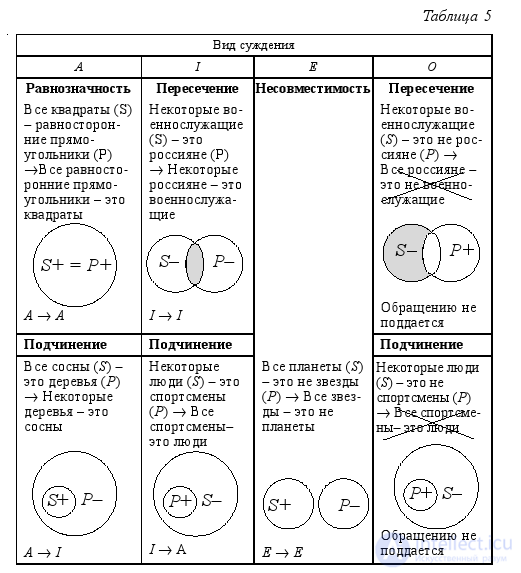
Суждение вида A обращается или в само себя, или в суждение вида I . Суждение вида I обращается или в само себя, или в суждение вида A . Суждение вида E всегда обращается в само себя, а суждение вида O не поддаётся обращению.
Второй способ преобразования простых суждений, называемый превращением ( обверсией ), заключается в том, что у суждения меняется связка: положительная на отрицательную, или наоборот. При этом предикат суждения заменяется противоречащим понятием (т. е. перед предикатом ставится частица «не»). Например, то же самое суждение, которое мы рассматривали в качестве примера для обращения: « Все акулы являются рыбами », – преобразуется путём превращения в суждение: « Все акулы не являются не рыбами ». Это суждение может показаться странным, ведь обычно так не говорят, хотя на самом деле перед нами более короткая формулировка той мысли, что ни одна акула не может быть таким существом, которое не является рыбой, или что множество всех акул исключается из множества всех существ, которые не являются рыбами. Субъект « акулы » и предикат « не рыбы » суждения, получившегося в результате превращения, находятся в отношении несовместимости.
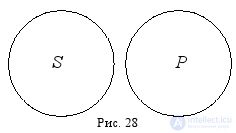
Приведённый пример превращения демонстрирует важную логическую закономерность: любое утверждение равно двойному отрицанию, и наоборот. Как видим, исходное суждение вида A в результате превращения стало суждением вида E . В отличие от обращения превращение не зависит от характера отношений между субъектом и предикатом простого суждения. Поэтому суждение вида A всегда превращается в суждение вида E , а суждение вида E – в суждение вида A . Суждение вида I всегда превращается в суждение вида O , а суждение вида O – в суждение вида I (рис. 28).
Третий способ преобразования простых суждений – противопоставление предикату – состоит в том, что сначала суждение подвергается превращению, а потом обращению. Например, чтобы путём противопоставления предикату преобразовать суждение: « Все акулы являются рыбами », – надо сначала подвергнуть его превращению. Получится: « Все акулы не являются не рыбами ». Теперь надо совершить обращение с получившимся суждением, т. е. поменять местами его субъект « акулы » и предикат « не рыбы ». Чтобы не ошибиться, вновь прибегнем к установлению распределённости терминов с помощью круговой схемы (субъект и предикат в этом суждении находятся в отношении несовместимости) (рис. 29):
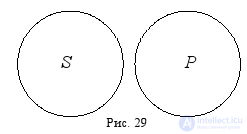
На круговой схеме видно, что и субъект, и предикат распределены (и тому, и другому термину соответствует полный круг), следовательно, мы должны сопроводить как субъект, так и предикат квантором « все ». После этого совершим обращение с суждением: « Все акулы не являются не рыбами ». Получится: « Все не рыбы не являются акулами ». Суждение звучит непривычно, однако это – более короткая формулировка той мысли, что если какое-то существо не является рыбой, то оно никак не может быть акулой, или что все существа, которые не являются рыбами, автоматически не могут быть и акулами в том числе. Обращение можно было сделать и проще, посмотрев в табл. 5 для обращения, которая приведена выше. Увидев, что суждение вида E всегда обращается в само себя, мы могли, не используя круговой схемы и не устанавливая распределённости терминов, сразу поставить перед предикатом « не рыбы » квантор « все ». В данном случае был предложен другой способ, чтобы показать, что вполне можно обойтись без табл. для обращения, и запоминать её совсем необязательно. Здесь происходит примерно то же самое, что и в математике: можно запоминать различные формулы, но можно обойтись и без запоминания, т. к. любую формулу нетрудно вывести самостоятельно.
Все три операции преобразования простых суждений проще всего совершать с помощью круговых схем. Для этого надо изобразить три термина: субъект, предикат и понятие, противоречащее предикату (непредикат). Потом следует установить их распределённость, и из получившейся схемы Эйлера будут вытекать четыре суждения – одно исходное и три результата преобразований. Главное, помнить, что распределённый термин соответствует квантору « все », а нераспределённый – квантору « некоторые »; что соприкасающиеся на схеме Эйлера круги соответствуют связке « является », а несоприкасающиеся – связке « не является ». Например, требуется совершить три операции преобразования с суждением: « Все учебники являются книгами ». Изобразим субъект « учебники », предикат « книги » и непредикат « не книги » круговой схемой и установим распределённость этих терминов (рис. 30):
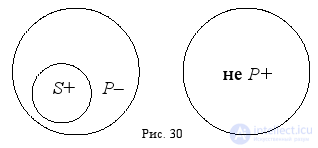
Получившуюся круговую схему можно прочитать четырьмя способами:
1. Все учебники являются книгами (исходное суждение).
2. Некоторые книги являются учебниками (обращение).
3. Все учебники не являются не книгами (превращение).
4. Все не книги не являются учебниками (противопоставление предикату).
Рассмотрим ещё один пример. Надо преобразовать тремя способами суждение: « Все планеты не являются звёздами ». Изобразим кругами Эйлера субъект « планеты », предикат « звёзды » и непредикат « не звёзды ». Обратите внимание на то, что понятия « планеты » и « не звёзды » находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой – это не обязательно планета. Установим распределённость этих терминов (рис. 31):
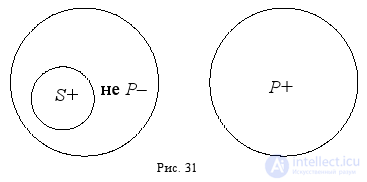
Получившуюся круговую схему можно прочитать четырьмя разными способами:
1. Все планеты не являются звёздами (исходное суждение).
2. All stars are not planets (appeal).
3. All planets are not stars (transformation).
4. Some non-stars are planets (opposition to predicate).
1. How is the treatment operation? Take some three judgments and make an appeal to each of them. How does the appeal occur in all kinds of simple judgments and in all cases the relationship between their subject and the predicate? What judgments are not amenable to appeal?
2. What is transformation? Take any three judgments and complete a transformation with each of them.
3. What is the operation of opposition to the predicate? Take three judgments and transform each of them by contrasting with the predicate.
4. Каким образом знания о распределённости терминов в простых суждениях и умение её устанавливать с помощью круговых схем может помочь в проведении операций преобразования суждений?
5. Возьмите какое-нибудь суждение вида A и совершите с ним все операции преобразования с помощью круговых схем и установления распределённости терминов. Сделайте то же самое с каким-нибудь суждением вида E .
Comments
To leave a comment
Logics
Terms: Logics