Lecture
Depending on the union through which simple judgments are combined into complex ones, five types of complex judgments are distinguished:
1. Conjunctive judgment (conjunction) is a complex judgment with a connecting union “and”, which in the logic is designated by the symbol “∧”. With the help of this sign, a conjunctive judgment consisting of two simple judgments can be represented as a formula: a ∧ b (read “ a and b ”), where a and b are two simple judgments. For example, a complex judgment: “ Lightning flashed, and thunder rumbled, ” is a conjunction (combination) of two simple judgments: “Lightning flashed,” “Thunder rumbled . ” A conjunction may consist not only of two, but also of a greater number of simple judgments. For example: " Lightning flashed, and thunder crashed, and it started to rain ( a ∧ b ∧ c )".
2. Disjunctive judgment (disjunction) is a complex judgment with the “or” dividing union. Recall that, speaking of the logical operations of addition and multiplication of concepts, we noted the ambiguity of this union - it can be used both in a non-strict (non-exclusive) meaning, and in a strict (exclusive) one. It is not surprising, therefore, that disjunctive judgments are divided into two types:
1. A non-strict disjunction is a complex proposition with the dividing union “or” in its lax (non-exclusive) meaning, which is denoted by the “∨” conventional symbol. With this sign, a loosely disjunctive judgment consisting of two simple judgments can be represented as a formula: a ∨ b (read “ a or b ”), where a and b are two simple judgments. For example, a difficult proposition: “ He studies English, or he studies German ,” is a lax disjunction (division) of two simple propositions: “He studies English,” “He studies German.” These judgments do not exclude each other, because it is possible to study both English and German at the same time, therefore this disjunction is not strict.
2. A strict disjunction is a complex judgment with the dividing union “or” in its strict (exclusive) meaning, which is denoted by the conventional sign “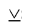 
". Using this sign, a strict disjunctive judgment, consisting of two simple judgments, can be represented as a formula: a
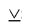b (read “either a or b ”), where a and b are two simple judgments. For example, a complex judgment: “ He studies in grade 9, or he learns in grade 11 ,” is a strict disjunction (separation) of two simple judgments: “He learns in grade 9,” “He learns in grade 11” . We draw attention to the fact that these judgments exclude each other, because it is impossible to study at the same time in 9 and 11 grade (if he learns in grade 9, then he definitely does not learn in grade 11, and vice versa), so this disjunction is strict.
Both lax and strict disjunctions can consist of not only two, but also of a greater number of simple judgments. For example: “ He learns English, or he learns German, or he learns French (a ∨ b ∨ c) ”, “ He studies in grade 9, or he learns in grade 10, or he learns in grade 11 (a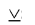
b
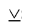c) ".
3. Implicative judgment (implication) is a complex judgment with the conditional union “if ... then”, which is denoted by the symbol “→”. With this sign, an implicative proposition consisting of two simple propositions can be represented as a formula: a → b (read “if a , then b ”), where a and b are two simple judgments. For example, a complex judgment: “ If a substance is a metal, then it is electrically conductive ,” is an implicative judgment (a causal link) of two simple judgments: “A substance is a metal”, “A substance is electrically conductive . ” In this case, these two judgments are connected in such a way that the second follows from the first one (if the substance is metal, then it is necessarily conductive), but the first does not follow from the second one (if the substance is electrically conductive, then this does not mean that it is a metal). The first part of the implication is called the base , and the second is the effect ; the corollary follows from the base, but the base does not follow from the corollary. The implication formula: a → b , can be read like this: “if a , then b is necessary, but if b , then a is not necessary”.
4. Equivalent judgment (equivalence) is a complex judgment with the union “if ... then” not in its conditional meaning (as in the case of implication), but in the identity (equivalent). In this case, this union is denoted by the symbol “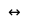 
", By which an equivalent judgment, consisting of two simple judgments, can be represented as a formula: a 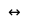b (read “if a , then b , and if b , then a ”), where a and b are two simple judgments. For example, a complex proposition: “ If a number is even, then it is divisible by 2 ”, is an equivalent judgment (equality, identity) of two simple judgments: “The number is even”, “The number is divisible by 2” . It is easy to notice that in this case the two judgments are connected in such a way that the second follows from the first and the first from the second: if the number is even, then it is necessarily divided without a balance by 2, and if the number is divided without a balance by 2, then it is necessarily even . It is clear that in an equivalent, in contrast to implication, there can be neither a basis nor a consequence, since its two parts are equivalent judgments.
5. Negative judgment (negation) is a complex judgment with the union “it is not true that ...”, which is denoted by the conventional sign “¬”. With this sign, a negative judgment can be represented as a formula: ¬ a (reads “it is not true that a ”), where a is a simple judgment. Here the question may arise - where is the second part of the complex judgment, which we usually denoted by the symbol b ? In the entry: ¬ a , there are already two simple judgments: a is some kind of statement, and the “¬” sign is its negation. We are confronted with two simple judgments, one affirmative, the other negative. An example of a negative judgment is: “ It is not true that all flies are birds .”
So, we have considered five types of complex judgments: conjunction, disjunction (non-strict and strict), implication, equivalence and denial.
There are many unions in natural language, but all of them are reduced in meaning to the five types considered, and any complex judgment relates to one of them. For example, a complex judgment: “ It is nearing midnight, but Herman is not there ,” is a conjunction, because in it the union “ a ” is used as a connecting union “and”. Complicated judgment, in which there is no union at all: “ Sow the wind, reap the storm, ” is an implication, since two simple judgments in it are connected in the sense of the conditional union “if ... then.”
Any complex judgment is true or false, depending on the truth or falsity of its simple judgments. Table is given. 6 truths of all types of complex judgments depending on all possible sets of truth values of two simple judgments within them (there are only four such sets): both simple judgments are true; the first judgment is true, and the second is false; the first judgment is false, and the second is true; both judgments are false).
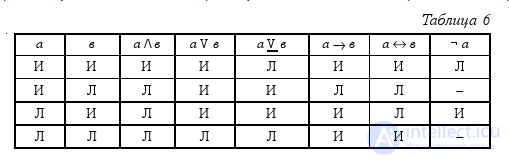
As we see, a conjunction is true only when both simple judgments that are included in it are true. It should be noted that the conjunction, consisting not of two, but of a greater number of simple judgments, is also true only in the case when all the judgments included in it are true. In all other cases, it is false. A non-strict disjunction, on the contrary, is true in all cases, except for the case when both simple judgments within it are false. A non-strict disjunction, consisting not of two, but of a greater number of simple judgments, is also false only if all simple judgments included in it are false. A strict disjunction is true only when one simple judgment is true, and the other is false. A strict disjunction, consisting not of two, but of a greater number of simple judgments, is true only if only one of its simple judgments is true, and all the others are false. Implication is false only in one case - when its foundation is true, and the consequence is false. In all other cases, it is true. The equivalence is true when the two components of its simple judgments are true or when both are false. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна. Проще всего определяется истинность отрицания: когда утверждение истинно, его отрицание ложно; когда утверждение ложно, его отрицание истинно.
1. На каком основании выделяются виды сложных суждений?
2. Охарактеризуйте все виды сложных суждений: название, союз, условное обозначение, формула, пример. Чем отличается нестрогая дизъюнкция от строгой? Как отличить импликацию от эквиваленции?
3. Каким образом можно определить вид сложного суждения, если в нём вместо союзов «и», «или», «если… то» употребляются какие-либо другие союзы?
4. Приведите по три примера для каждого вида сложных суждений, не используя при этом союзов «и», «или», «если…то».
5. Определите, к какому виду относятся следующие сложные суждения:
1. Живое существо является человеком только тогда, когда оно обладает мышлением.
2. Человечество может погибнуть то ли от истощения земных ресурсов, то ли от экологической катастрофы, то ли в результате третьей мировой войны.
3. Вчера он получил двойку не только по математике, но ещё и по русскому.
4. Проводник нагревается, когда через него проходит электрический ток.
5. Окружающий нас мир либо познаваем, либо нет.
6. Или же он совершенно бездарен, или же полный лентяй.
7. Когда человек льстит, он лжёт.
8. Вода превращается в лёд лишь при температуре от 0 °C и ниже.
6. От чего зависит истинность сложных суждений? Какие значения истинности принимают конъюнкция, нестрогая и строгая дизъюнкция, импликация, эквиваленция и отрицание в зависимости от всех наборов истинностных значений входящих в них простых суждений?
Comments
To leave a comment
Logics
Terms: Logics