Lecture
"One drop of water a person who can think logically can conclude that the Atlantic Ocean or Niagara Falls exists, even if he has not seen that other one and never heard of them ... On the nails of a person, on his hands, shoes, the fold of the trousers on the knees, on the thickening of the skin on the thumb and forefinger, on the expression of the face and the cuffs of the shirt — in such trifles it is not difficult to guess his profession. And there is no doubt that all this, taken together, will tell the competent observer the right conclusions. ”
This is a quote from a program article of the most famous detective-consultant Sherlock Holmes in the world literature. Based on the smallest details, he built logically impeccable chains of reasoning and uncovered intricate crimes, often without leaving his apartment on Baker Street. Holmes used the deductive method he had created himself, which, as his friend Dr. Watson suggested, would solve crimes to the edge of exact science.
Of course, Holmes somewhat exaggerated the value of deduction in criminalistics, according to his reasoning about the deductive method did the trick. “Deduction” from a special and only a little known term has turned into a commonly used and even fashionable concept. The popularization of the art of correct reasoning, and, above all, deductive reasoning, is no less a merit of Holmes than all the crimes he uncovered. He managed to “give logic the beauty of a dream, wading through the crystal labyrinth of possible deductions to a single brilliant conclusion” (V. Nabokov).
Deduction is a special case of inference.
In a broad sense, inference is a logical operation, as a result of which from one or several accepted assertions (assumptions) we get a new statement (conclusion, consequence).
Depending on whether there is a connection between logical premise and conclusion of logical following, two kinds of conclusions can be distinguished.
The basis of deductive reasoning is a logical law, whereby the conclusion with logical necessity follows from the accepted assumptions.
A distinctive feature of such a conclusion is that it always leads to a true conclusion from true premises.
In inductive reasoning, the connection between premises and conclusions is not based on the law of logic, but on some factual or psychological grounds that are not of a purely formal nature.
In such a conclusion, the conclusion does not follow logically from the premises and may contain information that is missing from them. The reliability of the premises therefore does not mean the reliability of the inductively derived from them. Induction will give only plausible, or plausible, conclusions that need further verification.
By deductive include, for example, such conclusions:
If it rains, the ground is wet. It's raining.
The earth is wet.
If helium is metal, it is electrically conductive. Helium is not electrically conductive.
Helium is not metal.
The line separating the premise from the conclusion replaces, as usual, the word "therefore."
Examples of induction are:
Argentina is a republic; Brazil is a republic; Venezuela is a republic; Ecuador is a republic. Argentina, Brazil, Venezuela, Ecuador - Latin American states.
This means that all Latin American states are republics.
Italy - Republic, Portugal - Republic, Finland - Republic, France - Republic.
Italy, Portugal, Finland, France - Western European countries.
Consequently, all Western European countries are republics.
Induction does not give a full guarantee of obtaining a new truth from the existing ones. The maximum that can be talked about is a certain degree of probability of the statement to be output. So the premisses of both the first and second inductive conclusions are true, but the conclusion of the first one is true, and the second one is false. Indeed, all Latin American states are republics; but among the West European countries there are not only republics, but also monarchies, for example, England, Belgium and Spain. Particularly characteristic deductions are logical transitions from general to particular knowledge, such as:
All metals are plastic. Copper is metal.
Consequently, copper is ductile.
In all cases when it is necessary to consider some phenomena on the basis of the already known general rule and to derive the necessary conclusion regarding these phenomena, we deduce in the form of deduction. The reasoning leading from knowledge about a part of objects (private knowledge) to knowledge about all objects of a certain class (general knowledge) is typical inductions. There always remains the possibility that the generalization will be hasty and unreasonable (“Napoleon is a commander; Suvorov is a commander; it means that every person is a commander”).
At the same time, it is impossible to identify deduction with the transition from the general to the particular, and induction with the transition from the particular to the general.
In the discourse, “Shakespeare wrote sonnets; therefore, it is not true that Shakespeare did not write sonnets ”is deduction, but there is no transition from the general to the particular. The argument “If aluminum is plastic or clay is plastic, then aluminum is plastic” is, as is commonly believed, inductive, but there is no transition from the particular to the general.
Deduction is the derivation of conclusions that are as reliable as the assumptions taken, induction - the extraction of probable (plausible) conclusions. Inductive conclusions include both transitions from the particular to the general, as well as analogy, methods for establishing causal relationships, confirmation of consequences, targeted justification, etc.
The particular interest that is manifested in deductive conclusions is understandable. They allow one to receive new truths from already existing knowledge, and moreover with the help of pure reasoning, without recourse to experience, intuition, common sense, etc. Deduction provides an absolute guarantee of success, and not just provides one or another, perhaps high, probability of a true conclusion. Going from the true premises and arguing deductively, we will in all cases get reliable knowledge.
Stressing the importance of deduction in the process of unfolding and justifying knowledge, one should not, however, detach it from induction and underestimate the latter. Almost all the general provisions, including scientific laws, are the results of inductive generalization. In this sense, induction is the basis of our knowledge. In and of itself, it does not guarantee its truth and validity, but it creates assumptions, links them with experience, and thereby informs them of a certain likelihood, a more or less high degree of probability. Experience is the source and foundation of human knowledge. Induction, departing from that which is apprehended in experience, is the necessary means of its generalization and systematization.
3.1. Inference as a form of thinking
Inference is a form of thinking in which from two or more judgments, called premises, follows a new judgment, called conclusion (conclusion):
All living organisms eat moisture. All plants are living organisms. All plants eat moisture.
In the example above, the first two propositions are the premises, and the third is the conclusion. Packages must be true judgments and must be interconnected. If at least one of the packages is false, then the output is false:
All birds are mammals.
All sparrows are birds. All sparrows are mammals.
As we see, in the above example, the falsity of the first premise leads to a false conclusion, despite the fact that the second premise is true. If the premises are not related to each other, then it is impossible to make a conclusion from them. For example, from the following two premises no output follows:
All planets are celestial bodies. All pines are trees.
? Let us pay attention to the fact that inference consists of judgments, and judgments consist of concepts, that is, one form of thinking enters the other as an integral part.
All conclusions are divided into direct and indirect. In direct conclusions, the conclusion is made from a single premise. Examples of such conclusions are given:
All flowers are plants. Some plants are flowers. It is true that all flowers are plants. It is not true that some flowers are not plants.
It is not difficult to guess that the direct conclusions are already known to us operations of converting simple judgments and conclusions about the truth of simple judgments by a logical square. The first example of direct reasoning is the transformation of a simple judgment by inversion, and in the second example, the logical square from the truth of the judgment of the form A concludes that the judgment of the form O is false.
In mediated inference, the conclusion is made from several premises. For example:
All fish are living creatures. All crucians are fish. All crucians are living creatures.
Indirect conclusions are divided into three types:
1. Deductive conclusions (deduction) (from the Latin. Deductio - derivation) are conclusions in which a conclusion is drawn from a general rule for a particular case (a special case is derived from a general rule). For example:
All stars radiate energy. The sun is a star. The sun radiates energy.
As we see, the first premise is a general rule, from which (with the help of the second premise) a special case follows in the form of a conclusion: if all stars radiate energy, it means that the Sun also radiates it, because it is a star. In deduction, reasoning goes from the general to the particular, from the larger to the lesser, knowledge is narrowed, by virtue of which the deductive conclusions are reliable, that is, accurate, obligatory, necessary. Let's look again at the given example. Could a different conclusion flow from the two data packages, besides which one follows from them? Could not!
The resulting conclusion is the only one possible in this case. We depict the relationship between the concepts of which our reasoning consisted of Euler circles.
Volumes of three concepts: " stars " ( W ); “ Energy radiating bodies ” ( T ); " Sun " ( C ), schematically located as follows (Fig. 33):

If the volume of the concept of " stars " is included in the volume of the concept of " body radiating energy ", and the volume of the concept of " Sun " is included in the volume of the concept of " stars ", then the volume of the concept of " Sun " is automatically included in the volume of the concept of " body radiating energy " in the power of which deductive conclusion is credible.
The undoubted merit of deduction, of course, lies in the reliability of its findings. Recall the famous literary hero Sherlock Holmes used the deductive method in the detection of crimes. This means that he constructed his reasoning in such a way as to deduce the particular from the general. In one work, explaining to Dr. Watson the essence of his deductive method, he gives such an example. Around the killed Colonel Morena, Scotland Yard detectives discovered a smoked cigar and decided that the colonel smoked it before he died. However, he (Sherlock Holmes) irrefutably proves that Colonel Morin could not smoke this cigar, because he wore large, bushy mustaches, and the cigar was smoked to the end, i.e., if it were smoked by Colonel Morin, then he certainly burned have your mustache. Consequently, another person smoked a cigar. In this reasoning, the conclusion looks convincing precisely because it is deductive: from the general rule:
“ Anyone with a big, bushy mustache cannot smoke a cigar to the end ,” says a special case: “ Colonel Moren could not smoke a cigar to the end because he wore such mustaches .”
We will consider the considered reasoning to the standard form of recording of inferences in the form of assumptions and output taken in logic:
Anyone with a big, bushy mustache can not smoke a cigar to the end. Colonel Morin wore a large, bushy mustache. Colonel Morin could not smoke a cigar to the end.
2. Inductive conclusions (induction) (from the Latin. Inductio - guidance) are conclusions in which a general rule is derived from several particular cases (a few private cases, as it were, suggest a general rule). For example:
Jupiter is moving. Mars is moving. Venus is moving. Jupiter, Mars, Venus are planets. All planets are moving.
The first three premises are special cases, the fourth one brings them under one class of objects, unites them, and the conclusion refers to all objects of this class, that is, a certain general rule (arising from three special cases) is formulated. It is easy to see that inductive conclusions are constructed on the principle opposite to the construction of deductive conclusions. In induction, reasoning goes from the particular to the general, from the smallest to the larger, knowledge expands, which is why inductive conclusions, unlike deductive ones, are not reliable, but probabilistic. In the induction example considered above, the feature found on some objects of some group has been transferred to all objects of this group, a generalization has been made, which is almost always fraught with an error: there may be some exceptions in the group, and even if many objects from a certain group characterized by some sign, it does not mean with certainty that all objects of this group are characterized by this sign. The probabilistic nature of the conclusions is, of course, a lack of induction. However, its undoubted advantage and advantageous difference from deduction, which is a narrowing knowledge, lies in the fact that induction is expanding knowledge that can lead to new things, while deduction is an analysis of the old and the already known.
3. Inference by analogy (analogy) (from the Greek. Analogia - correspondence) is the conclusion in which, based on the similarity of objects (objects) in some signs, it is concluded that they are similar in other signs. For example:
Planet Earth is located in the solar system, it has an atmosphere, water and life. Planet Mars is located in the solar system, it has an atmosphere and water. There is probably life on Mars.
As you can see, two objects are compared (compared) (planet Earth and planet Mars), which are similar to each other in some essential, important features (to be in the solar system, to have an atmosphere and water). Based on this similarity, it is concluded that, perhaps, these objects are similar to each other and in other signs: if there is life on Earth, and Mars is in many ways similar to Earth, then there is a possibility of life on Mars. The conclusions of the analogy, like the conclusions of induction, are probabilistic.
1. What is the conclusion? Why should the premise of conclusions be true and interconnected judgments?
2. What is the difference between direct reasoning and indirect ones? Give three examples of direct and indirect inferences.
3. What are deductive conclusions? Why are the deduction conclusions reliable?
4. What is inductive reasoning? What is the difference between induction and deduction? What is the reason for the probabilistic nature of the inductive conclusions?
5. How are inference built by analogy? How do they differ from deductive and inductive conclusions?
3.2. Figures and modes of simple syllogism
All deductive conclusions are called syllogisms (from the Greek. Sillogismos - counting, summarizing, deducing the effect). There are several types of syllogisms. The first of them is called simple ( categorical ), because all judgments included in it (two assumptions and conclusion) are simple, or categorical. These are already known to us judgments of types A , I , E , O.
Consider an example of a simple syllogism:
All flowers ( M ) are plants ( P ).
All roses ( S ) are flowers ( M ).
All roses ( S ) are plants ( P ). Both premises and conclusion are simple judgments in this syllogism (and the premises and conclusion are judgments of the form A (general affirmative)). We draw attention to the conclusion presented by the proposition: " All roses are plants ." In this conclusion, the subject is the term " roses ", and the predicate is the term " plants ". The subject of the conclusion is present in the second premise of the syllogism, and the predicate of the conclusion is in the first. Also in both premises the term “ flowers ” is repeated, which, as it is not difficult to see, is a binding: it is thanks to it that the unrelated, disconnected in the premises the terms “ plants ” and “ roses ” can be linked in the conclusion. Thus, the structure of the syllogism includes two premises and one conclusion, which consist of three (variously arranged) terms:
1. The subject of the conclusion is located in the second premise of the syllogism and is called the lesser term of the syllogism (the second premise is also called the lesser).
2. The predicate of the conclusion is located in the first premise of the syllogism and is called the big term of the syllogism (the first premise is also called the greater one). As a rule, the predicate of inference is a larger concept than the subject of inference (in the example given, the concepts of “ roses ” and “ plants ” are in relation to generic subordination), which is why the predicate of inference is called a larger term, and the subject of inference is a lesser term.
3. Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизма и обозначается латинской буквой М , потому что «средний» на латинском – это medium .
Три термина силлогизма могут быть расположены в нём по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма . Таких фигур четыре, т. е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Consider them.
Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. For example:
Все газы ( М ) – это химические элементы ( Р ).
Гелий ( S ) – это газ ( М ).
Гелий ( S ) – это химический элемент ( Р ). Учитывая, что в первой посылке средний термин связан с предикатом, во второй субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведённом примере (рис. 34):

The straight lines in the diagram (with the exception of the one that separates the premisses from the conclusion) show the connection of terms in the premises and in the conclusion. Since the role of the middle term is to connect the larger and the smaller terms of the syllogism, on the diagram the middle term in the first premise is connected with the middle term in the second premise. The diagram shows exactly how the middle term connects other terms of the syllogism in its first figure. In addition, the relationship between the three terms can be depicted using Euler circles. In this case, we get the following scheme (Fig. 35):

The second figure of the syllogism is the arrangement of its terms, in which both the first and the second premises end with an average term. For example:
All fish ( P ) breathe with gills ( M ).
All whales ( S ) do not breathe in the gills ( M ) . All whales ( s ) are not fish ( p ).
The schemes of mutual arrangement of terms and relations between them in the second figure of the syllogism look like this (Fig. 36):

The third figure of a syllogism is the arrangement of its terms, in which both the first and second premises begin with the middle term. For example:
All tigers ( M ) are mammals ( P ).
All tigers ( M ) are predators ( S ).
Some predators ( S ) are mammals ( P ). Schemes of mutual arrangement of terms and relations between them in the third figure of the syllogism (Fig. 37):

The fourth figure of the syllogism is the arrangement of its terms, in which the first premise ends in an average term, and the second begins with it. For example:
All squares ( P ) are rectangles ( M ).
All rectangles ( M ) are not triangles ( S ).
Все треугольники ( S ) – это не квадраты ( Р ). Схемы взаимного расположения терминов и отношений между ними в четвёртой фигуре силлогизма (рис. 38):

Отметим, что отношения между терминами силлогизма во всех фигурах могут быть и другими.
Любой простой силлогизм состоит из трёх суждений (двух посылок и вывода). Каждое из них является простым и принадлежит к одному из четырёх видов ( A , I , E , O ). Набор простых суждений, входящих в силлогизм, называется модусом простого силлогизма .
For example:
Все небесные тела движутся. Все планеты – это небесные тела. Все планеты движутся.
В силлогизме первая посылка является простым суждением вида A (общеутвердительным), вторая посылка – это тоже простое суждение вида A , и вывод в данном случае представляет собой простое суждение вида A . Поэтому рассмотренный силлогизм имеет модус AАA .
Во втором примере: Все журналы – это периодические издания. Все книги не являются периодическими изданиями. Все книги не являются журналами. Силлогизм имеет модус AEE. В третьем примере: Все углероды – простые тела. Все углероды электропроводны. Некоторые электропроводники – простые тела.
Силлогизм имеет модус AAI . Всего модусов во всех четырёх фигурах, т. е. возможных комбинаций простых суждений в силлогизме, – 256. В каждой фигуре 64 модуса. Однако из этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность её выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные – неправильными.
Наша задача – уметь определять фигуру и модус любого простого силлогизма. Например, требуется установить фигуру и модус силлогизма:
Все вещества состоят из атомов. Все жидкости – это вещества. Все жидкости состоят из атомов.
Прежде всего надо найти субъект и предикат вывода, т. е. меньший и больший термины силлогизма. Далее следует установить местоположение меньшего термина во второй посылке и большего – в первой. После этого можно определить средний термин и схематично изобразить расположение всех терминов в силлогизме (рис. 39):

Все вещества ( М ) состоят из атомов ( Р ).
Все жидкости ( S ) – это вещества ( М ).
Все жидкости ( S ) состоят из атомов ( Р ). Как видим, рассматриваемый силлогизм построен по первой фигуре. Теперь надо найти его модус. Для этого следует выяснить, к какому виду простых суждений относятся первая и вторая посылки и вывод. В нашем примере обе посылки и вывод являются суждениями вида A (общеутвердительными), т. е. модус данного силлогизма – AАA . Итак, предложенный силлогизм имеет первую фигуру и модус AАA .
1. Что такое силлогизм?
2. Какова структура простого силлогизма?
3. What is a simple syllogism figure? Think about why there are only four figures of the syllogism? How to determine the shape of the proposed syllogism? Give two examples for each syllogism figure, accompanying them with diagrams of the relative position of the terms and the relations between them.
4. What is a simple syllogism mode? How to determine the modus of the proposed syllogism? How many modes exist in all four syllogism figures? What are right and wrong modes? How many correct modes are there? Bring, independently picked up, one example of syllogisms with modes AAA, AEE, AAI.
5. Determine the shape and mode of the following syllogisms:
1) All snakes are reptiles. All reptiles are not invertebrates. All invertebrates are not terrible.
2) All pines are coniferous trees. No birch is a coniferous tree. No birch is a pine.
3) All bees are insects. All bees are flying creatures. Some flying creatures are insects.
4) No elementary particle is a molecule. All electrons are elementary particles. No electron is a molecule.
5) All majors are military personnel. Some Russians are majors. Some Russians are servicemen.
3.3. General rules of simple syllogism
The rules of the syllogism are divided into general and particular.
The general rules apply to all simple syllogisms, no matter what shape they are built on.
The particular rules are valid only for each syllogism figure and are therefore often referred to as shape rules.
Consider the general rules of syllogism:
1. There should be only three terms in syllogism . Let us turn to the already mentioned example of the syllogism, in which this rule is violated:
Movement forever. Going to school is a movement. Going to school forever.
Both premises of this syllogism are true judgments, but a false conclusion follows from them, because the rule in question has been violated. The word “ movement ” is used in two premises in two different meanings: movement as a universal world change and movement as a mechanical movement of a body from point to point. It turns out that there are three terms in syllogism: movement, going to school, eternity , and there are four meanings (since one of the terms is used in two different senses), that is, an extra meaning implies an extra term. In other words, in the given example, the syllogism had not three, but four (within the meaning) terms. An error that occurs when the above rule is violated is called quadrupling of terms .
2. The middle term should be distributed in at least one of the premises . The distribution of terms in simple judgments was discussed in the previous chapter. Recall that the easiest way to establish the distribution of terms in simple judgments is with the help of circular schemes: it is necessary to depict the relations between the terms of the judgment in Euler circles, while the complete circle in the diagram will denote the distributed term (+), and the incomplete one - unallocated (-). Consider the example of a syllogism:
All cats (K) are living creatures (J. p.). Socrates (C) is also a living being. Socrates is a cat.
False conclusion follows from the two true premises. Let us draw the circles between the terms in the syllogism premises by circles of Euler and establish the distribution of these terms (Fig. 40):
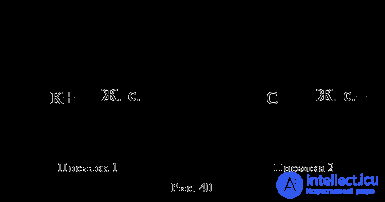
Как видим, средний термин (« живые существа ») в данном случае нераспределён ни в одной из посылок, а по правилу он должен быть распределён хотя бы в одной. Ошибка, возникающая при нарушении рассматриваемого правила, так и называемая – нераспределённость среднего термина в каждой посылке .
3. Термин, который был не распределён в посылке, не может быть распределён в выводе . Обратимся к следующему примеру:
Все яблоки (Я) – съедобные предметы (С. п.). Все груши (Г) – это не яблоки. Все груши – несъедобные предметы.
Посылки силлогизма являются истинными суждениями, а вывод – ложным. Как и в предыдущем случае, изобразим кругами Эйлера отношения между терминами в посылках и в выводе силлогизма и установим распределённость этих терминов (рис. 41):
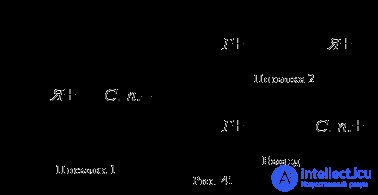
В данном случае предикат вывода, или больший термин силлогизма (« съедобные предметы »), в первой посылке является нераспределённым (–), а в выводе – распределённым (+), что запрещается рассматриваемым правилом. Ошибка, возникающая при его нарушении, называется расширением большего термина . Вспомним, что термин распределён, когда речь идёт обо всех предметах, входящих в него, и не распределён, когда речь идёт о части предметов, входящих в него, именно поэтому ошибка и называется расширением термина.
4. В силлогизме не должно быть двух отрицательных посылок . Хотя бы одна из посылок силлогизма должна быть положительной (могут быть положительными и обе посылки). Если две посылки в силлогизме отрицательные, то вывод из них или вообще сделать нельзя, или же, если его сделать возможно, он будет ложным или, по крайней мере, недостоверным, вероятностным. For example:
Снайперы не могут иметь плохое зрение. Все мои друзья – не снайперы. Все мои друзья имеют плохое зрение.
Обе посылки в силлогизме являются отрицательными суждениями, и, несмотря на их истинность, из них вытекает ложный вывод.
Ошибка, которая возникает в данном случае, так и называется – две отрицательные посылки .
5. В силлогизме не должно быть двух частных посылок . Хотя бы одна из посылок должна быть общей (могут быть общими и обе посылки). Если две посылки в силлогизме представляют собой частные суждения, то вывод из них сделать невозможно. For example:
Некоторые школьники – это первоклассники. Некоторые школьники – это десятиклассники.
Из этих посылок никакой вывод не следует, потому что обе они являются частными. Ошибка, возникающая при нарушении данного правила, так и называется – две частные посылки .
6. Если одна из посылок отрицательная, то и вывод должен быть отрицательным . For example:
Ни один металл не является изолятором. Медь – это металл. Медь не является изолятором.
Как видим, из двух посылок данного силлогизма не может вытекать утвердительный вывод. Он может быть только отрицательным.
7. Если одна из посылок частная, то и вывод должен быть частным . For example:
Все углеводороды – это органические соединения. Некоторые вещества – это углеводороды. Некоторые вещества – это органические соединения.
В этом силлогизме из двух посылок не может следовать общий вывод. Он может быть только частным, т. к. вторая посылка является частной.
1. Что такое общие правила силлогизма?
2. Каковы общие правила простого силлогизма? Приведите по два примера ошибок: учетверение терминов, нераспределённость среднего термина в посылках, расширение большего термина, две отрицательные посылки.
3. Нарушены ли какие-нибудь (и какие) общие правила в следующих силлогизмах:
1) Все травоядные питаются растительной пищей. Все тигры не питаются растительной пищей. Все тигры не являются травоядными.
2) Все отличники не получают двоек. Мой друг не отличник. Мой друг получает двойки.
3) Все рыбы плавают. Все киты тоже плавают. Все киты являются рыбами.
4) Лук – это древнее орудие для стрельбы. Одна из овощных культур – это лук. Одна из овощных культур – это древнее орудие для стрельбы.
5) Любой металл не является изолятором. Вода – это не металл. Вода является изолятором.
3.4. Виды сокращённого простого силлогизма
Простой силлогизм – это одна из широко распространённых разновидностей умозаключения. Поэтому он часто используется в повседневном и научном мышлении. Однако при его употреблении мы, как правило, не соблюдаем его жёсткую логическую структуру. For example:
Все рыбы не являются млекопитающими; а все киты являются млекопитающими. Следовательно, все киты не являются рыбами.
Вместо этого, мы, скорее всего, скажем: « Все киты не рыбы, так как они – млекопитающие », – или: « Все киты не рыбы, потому что рыбы – не млекопитающие». Нетрудно увидеть, что эти два умозаключения представляют собой сокращённую форму приведённого простого силлогизма.
Таким образом, в мышлении и речи обычно используется не простой силлогизм, а его различные сокращённые разновидности:
1. Энтимема – это простой силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что из любого силлогизма можно вывести три энтимемы. For example:
Все металлы электропроводны. Железо – это металл. Железо электропроводно.
Three enthymemes follow from this syllogism: “ Iron is electrically conductive because it is a metal (a large parcel is missed)”, “ Iron is electrically conductive because all metals are electrically conductive (a smaller parcel is omitted)”, “ All metals are electrically conductive, and iron is a metal ( missed output) ".
2. Epichureim is a simple syllogism, in which both premises are entimemes. Take two syllogisms and derive enthymemes from them.
Syllogism 1:
All that leads society to disaster is evil.
Social injustice leads society to disaster.
Social injustice is evil.
Skipping a big premise in this syllogism, we get entymem: “ Social injustice is evil, because it leads society to disaster .”
Syllogism 2:
All that contributes to the enrichment of some at the expense of the impoverishment of others - this is social injustice. Private property contributes to the enrichment of some due to the impoverishment of others. Private property is a social injustice.
Passing a big premise in this syllogism, we get entymem: “ Private property is a social injustice, since it contributes to the enrichment of some due to the impoverishment of others .” If we arrange these two entimemes one after another, they will become the premises of a new, third syllogism, which will be an epichaire:
Social injustice is evil because it leads society to disaster. Private property is a social injustice, as it contributes to the enrichment of some at the expense of the impoverishment of others. Private property is evil.
As we can see, three syllogisms can be distinguished in the epi-heirem: two of them are parcels, and one is built from the conclusions of parcel syllogisms. This last syllogism is the basis for the final conclusion.
3. Polysillogism (complex syllogism) is two or more simple syllogisms, interconnected in such a way that the conclusion of one of them is the premise of the next.
For example:
Anything that develops thinking is helpful. All intellectual games develop thinking. All intellectual games are useful. Chess is an intellectual game. Chess is useful.
Two syllogisms united in polysillogism are highlighted with parentheses. We draw attention to the fact that the conclusion of the previous syllogism was the larger premise of the subsequent one. In this case, the resulting polysillogism is called progressive . If the output of the previous syllogism becomes the smaller premise of the subsequent one, then the polysillogism is called regressive .
For example:
All stars are celestial bodies. The sun is a star. The sun is a heavenly body. All celestial bodies are involved in gravitational interactions. The sun is a heavenly body. The sun is involved in gravitational interactions.
The conclusion of the previous syllogism is the lesser premise of the following. It can be noted that in this case the two syllogisms cannot be graphically connected in a coherent chain, as in the case of progressive polysillogism.
It was said above that polysillogism may consist not only of two, but also of a greater number of simple syllogisms. Let us give an example of polysillogism (progressive), which consists of three simple syllogisms:
All material has physical properties. All objects of the universe are material. All objects of the universe have physical properties. Quanta are objects of the universe. Quanta have physical properties. Photons are quanta of the electromagnetic field. Photons have physical properties.
4. Litter (a complex syllogism) is a polysillogism, in which the premise of the subsequent syllogism is missing, which is the conclusion of the previous one. Let us return to the example of progressive polysillogism discussed above and skip the large premise of the second syllogism, which is the conclusion of the first syllogism. It turns out progressive litters:
Anything that develops thinking is helpful. All intellectual games develop thinking. Chess is an intellectual game. Chess is useful.
Now let us turn to the example of regressive polysillogism discussed above and skip the smaller premise of the second syllogism, which is the conclusion of the first syllogism. Get regressive litters:
All stars are celestial bodies.
The sun is a star.
All celestial bodies are involved in gravitational interactions.
The sun is involved in gravitational interactions.
1. Why is simple syllogism not quite convenient for constant use in thought and speech? What is it usually replaced with?
2. What is entimmema? Why can three enthymemes be derived from any syllogism? Come up with some example of a simple syllogism and derive from it all the enthymeme.
3. What is epichureim? How many simple syllogisms implicitly form part of any epichaeremus? Try to come up with an example of some kind of epi-herem.
4. What is polysillogism? What is the difference between progressive polysillogism and regressive? Come up with one example for progressive and regressive polysillogism.
5. What is littering up? Which litters are progressive, and which - regressive? Come up with one example for progressive and regressive sorit.
3.5. Dividing and categorical and purely dividing syllogisms
Inference that contains the separation, (disjunctive) judgments are called separation . In thinking and speaking, a separating-categorical syllogism is often used, in which, as the name implies, the first premise is a separative (disjunctive) judgment, and the second premise is a simple (categorical) one. For example:
The school may be primary, or secondary, or higher. MSU is a higher education institution. MSU is not a primary or secondary school.
Separating-categorical syllogism has two modes:
1. An approvingly denying modus , in which the first premise is a strict disjunction of several variants of something, the second affirms one of them, and the conclusion denies all the others (thus, the argument moves from affirmation to denial). For example:
Forests are coniferous, or deciduous, or mixed. This forest is coniferous. This forest is not deciduous and not mixed.
With the help of symbols of logical unions, you can present the form of this syllogism in the form of the following entry:
(( a

b

c ) ∧ a ) → (¬ b ∧ ¬ c ), where ( a

b

c ) - this is the first premise in the form of a strict disjunction of three simple judgments; a is the second premise in the form of the statement of one of them; (( a

b

c ) ∧ a ) - these are two syllogism premises, connected by a conjunction sign; (¬ b ∧ ¬ c ) is the conclusion of the syllogism in the form of a conjunction of the negatives of the two remaining simple judgments that were part of the first premise; the implication sign “→” indicates that the output follows the output.
2. The negative-affirming mode , in which the first premise is a strict disjunction of several variants of something, the second denies all given variants but one, and the conclusion confirms the one remaining variant (thus, the argument moves from negation to affirmation).
For example:
People are Caucasians, or Mongoloids, or Negroids. This man is not a Mongoloid or Negroid. This person is Caucasian.
Using the notation of logical unions, you can present the form of this syllogism in the form of the following entry:
(( a

b

c ) ∧ (¬ b ∧ ¬ c )) → a , where ( a

b

c ) - this is the first premise in the form of a strict disjunction of three simple judgments; (¬ b ∧¬ c ) is the second premise in the form of a conjunction of the negatives of two of them;
( a

b

c ) ∧ (¬ b ∧¬ c ) - these are two syllogism premises, connected by a conjunction sign; a is the conclusion of the syllogism in the form of a statement of the third simple proposition that was part of the first premise; and finally, the implication unites the premises and the conclusion of the syllogism.
The first premise of the separation-categorical syllogism is a strict disjunction, that is, it is a logical operation of dividing a concept that is already familiar to us. Therefore, it is not surprising that the rules of this syllogism repeat the rules of division of the concept known to us:
1. The division in the first parcel should be made on one basis . For example:
Transport is ground, or underground, or water, or air, or public. Suburban electric trains are public transport. Suburban electric trains are not land, not underground, not water and not air transport.
The syllogism is constructed in an affirmatively denying mode: in the first premise several options are presented, in the second premise one of them is asserted, which is why all others are denied in the inference. However, a false conclusion follows from the two true premises. Why is this so? Because in the first premise the division was carried out for two different reasons: in which natural environment the transport moves and to whom it belongs. The substitution of the base of division in the first premise of the categorical syllogism leads to a false conclusion.
2. The division in the first parcel must be complete . For example:
Mathematical actions are addition, or subtraction, or multiplication, or division. Logarithm is not addition, not subtraction, not multiplication, and not division. Logarithm is not a mathematical operation.
In syllogism, the incomplete division in the first premise leads to a false conclusion, which follows from the true premises.
3. The results of the division in the first premise should not intersect, or the disjunction should be strict . For example:
The countries of the world are northern, or southern, or western, or eastern. Canada is a northern country. Canada is not southern, not western and not eastern country.
In syllogism, the conclusion is false, because Canada is as much a northern country as a western one. The false conclusion for true assumptions is explained in this case by the intersection of the results of the division in the first premise, or, which is the same thing, by a loose disjunction . It should be noted that a non-strict disjunction in the separation-categorical syllogism is permissible in the case when it is built according to the denying-approving modus. For example:
He is strong by nature or constantly engaged in sports. He is not strong by nature. He is constantly involved in sports.
There is no error in the syllogism, despite the fact that the disjunction in the first package was not strict. Thus, the considered rule is unconditionally valid only for the affirmative-denying mode of the separation-categorical syllogism.
4. The division in the first parcel should be consistent . For example:
Proposals are simple, or complex, or complex.
This sentence is complex. This proposal is not simple and not complicated.
In syllogism, a false conclusion follows from the true premises for the reason that a jump in division was made in the first premise.
The separation-categorical syllogism in logic is often called simply the separation-categorical inference. In addition to it, there is also a purely separative syllogism ( purely separative reasoning) , both premises and the conclusion of which are separative (disjunctive) judgments.
For example:
Mirrors are flat or spherical. Spherical mirrors are concave or convex. Mirrors are flat, or concave, or convex.
The form of a purely separating syllogism can be represented as follows: (( a

b ) ∧ ( b 1

b 2 )) → ( a

b 1

b 2 ) where ( a

b ) - the first parcel; ( b 1

b 2 ) - the second premise; ( a

b 1

b 2 ) - conclusion.
1. What are the separation conclusions?
2. What modes has a categorical syllogism?
Give three examples for each modus, depicting their form using conventional logical symbols.
3. What are the rules of the categorical syllogism?
What mistakes occur when they are violated? In which case can a disjunction in a categorical syllogism be lax? Come up with one example for each error that occurs when a rule is violated.
4. What is the difference between a purely separative syllogism and a categorical syllogism? Give two examples of a purely separative syllogism.
5. Are there any mistakes (and what) in the following categorical syllogisms:
1. Quadrilaterals are squares, or rhombus, or trapezoid. This figure is not a rhombus or trapezium. This figure is a square.
2. Selection in wildlife is artificial or natural. This selection is not artificial. This selection is natural.
3. People are talented, or untalented, or stubborn.
He is a stubborn man.
He is not talented and not mediocre.
4. Judgments are affirmative or negative.
This judgment is affirmative.
This judgment is not negative.
5. Students are excellent students or losers.
My friend is not an excellent student.
My friend - Losers.
3.6. Conditionally categorical, equivalent categorical and purely conditional syllogisms
Inference that contains conditional (implicative) judgments are called conditional . In thinking and speaking, conditional categorical syllogism is often used, the name of which indicates that in it the first premise is a conditional (implicative) judgment, and the second premise is a simple (categorical) one. For example:
If the runway is covered with ice, the planes can not take off.
Today, the runway is covered with ice.
Today, the aircraft can not take off.
The conditionally categorical syllogism has two modes:
1. The approving modus , in which the first premise is an implication, consisting, as we already know, of two parts - the base and the effect, the second premise is the statement of the base, and the conclusion is asserted in the conclusion. For example:
If the substance is metal, then it is electrically conductive.
This substance is metal.
This substance is electrically conductive.
Форма утверждающего модуса условно-категорического силлогизма: (( a → b ) ∧ a ) → b , где ( a → b ) – это первая посылка в виде импликации основания и следствия; (( a → b ) ∧ a ) – это две посылки силлогизма в виде двухчленной конъюнкции, состоящей из уже упомянутой импликации и утверждения основания; b – это вытекающий из посылок вывод силлогизма в виде утверждения следствия.
2. Отрицающий модус , у которого первая посылка представляет собой импликацию основания и следствия, вторая посылка является отрицанием следствия, а в выводе отрицается основание.
For example:
Если вещество – металл, то оно электропроводно.
Данное вещество неэлектропроводно.
Данное вещество – не металл.
Форма отрицающего модуса условно-категорического силлогизма: (( a → b ) ∧¬ b ) → ¬ a , где ( a → b ) – это первая посылка в виде импликации основания и следствия; (( a → b ) ∧ ¬ b ) – это две посылки силлогизма в виде двухчленной конъюнкции, состоящей из уже упомянутой импликации и отрицания следствия; ¬ a – это вытекающий из посылок вывод силлогизма в виде отрицания основания.
Необходимо обратить внимание на уже известную нам особенность импликативного суждения, которая состоит в том, что основание и следствие нельзя поменять местами. Например, высказывание: « Если вещество – металл, то оно электропроводно », – является верным, т. к. все металлы – это электропроводники (из того, что вещество – металл, с необходимостью вытекает его электропроводность). Однако высказывание: « Если вещество электропроводно, то оно – металл », – неверно, т. к. не все электропроводники являются металлами (из того, что вещество электропроводно, не вытекает то, что оно – металл). Эта особенность импликации обусловливает два правила условно-категорического силлогизма:
1. Утверждать можно только от основания к следствию , т. е. во второй посылке утверждающего модуса должно утверждаться основание импликации (первой посылки), а в выводе – её следствие.
В противном случае из двух истинных посылок может вытекать ложный вывод. For example:
Если слово стоит в начале предложения, то его надо писать с большой буквы.
Слово «Москва» надо писать с большой буквы.
Слово «Москва» всегда стоит в начале предложения.
В силлогизме во второй посылке утверждалось следствие, а в выводе – основание: (( a → b ) ∧ b ) → a . Это утверждение от следствия к основанию и является причиной ложного вывода при истинных посылках.
2. Отрицать можно только от следствия к основанию , т. е. во второй посылке отрицающего модуса должно отрицаться следствие импликации (первой посылки), а в выводе – её основание. В противном случае из двух истинных посылок может вытекать ложный вывод. For example:
Если слово стоит в начале предложения, то его надо писать с большой буквы.
В данном предложении слово «Москва» не стоит в начале.
В данном предложении слово «Москва» не надо писать с большой буквы.
В силлогизме во второй посылке отрицается основание, а в выводе – следствие: (( a → b ) ∧ ¬ a ) → ¬ b . Это отрицание от основания к следствию и является причиной ложного вывода при истинных посылках.
Вспомним, что среди сложных суждений помимо импликации: a → b , есть также эквиваленция: a
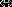
b . Если в импликации всегда выделяется основание и следствие, то в эквиваленции нет ни того, ни другого, т. к. она представляет собой сложное суждение, обе части которого тождественны (эквивалентны) друг другу. Если первой посылкой силлогизма является не импликация, а эквиваленция, то такой силлогизм называется эквивалентно-категорическим . For example:
Если число чётное, то оно делится без остатка на 2.
Число 16 – чётное.
Число 16 делится без остатка на 2.
Форма модуса данного силлогизма: ( a
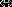
b ) ∧ a ) → b .
Поскольку в первой посылке эквивалентно-категорического силлогизма нельзя выделить ни основания, ни следствия, то рассмотренные выше правила условно-категорического силлогизма к нему неприменимы (в эквивалентно-категорическом силлогизме и утверждать, и отрицать можно как угодно). Если в условно-категорическом силлогизме два модуса правильных и два неправильных (см. выше), то в эквивалентно-категорическом силлогизме все четыре модуса являются правильными:
(( a
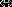
b ) ∧ a ) → b ;
(( a
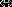
b ) ∧ b ) → a ;
(( a
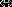
b ) ∧ ¬ a ) → ¬ b ;
(( a
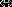
b ) ∧ ¬ b ) → ¬ a .
Читатель без труда сможет подобрать примеры для каждого из четырёх модусов эквивалентно-категорического силлогизма.
Если же обе посылки и вывод представляют собой условные суждения, то это чисто условный силлогизм (чисто условное умозаключение) . For example:
Если вещество является металлом, то оно электропроводно.
Если вещество электропроводно, то его невозможно использовать в качестве изолятора.
Если вещество является металлом, то его невозможно использовать в качестве изолятора.
Форма модуса данного силлогизма: (( a → b ) ∧ ( b → c )) → ( a → c ).
1. Что представляют собой условные умозаключения?
2. Какие модусы имеет условно-категорический силлогизм? Приведите по три примера для каждого модуса, изобразив их форму с помощью условных логических обозначений.
3. Что называется в условно-категорическом силлогизме «основанием», а что – «следствием»? Каковы правила условно-категорического силлогизма и ошибки, возникающие при их нарушении?
Придумайте по два примера для каждой ошибки, возникающей при нарушении соответствующего правила.
4. Что такое эквивалентно-категорический силлогизм? Чем он отличается от условно-категорического? Почему в условно-категорическом силлогизме только два модуса являются правильными, а в эквивалентно-категорическом – четыре. Придумайте по одному примеру для каждого модуса эквивалентно-категорического силлогизма.
5. Чем отличается чисто условный силлогизм от условно-категорического силлогизма? Приведите два примера чисто условного силлогизма.
6. Допущены ли ошибки (и какие) в следующих условно-категорических силлогизмах:
1) Если животное является млекопитающим, то оно позвоночное.
Рептилии не являются млекопитающими.
Рептилии не являются позвоночными.
2) Если человек льстит, то он лжёт.
Этот человек льстит.
Этот человек лжёт.
3) Если геометрическая фигура является квадратом, то у неё все стороны равны.
Равносторонний треугольник не является квадратом.
У равностороннего треугольника стороны не равны.
4) Если металл – свинец, то он тяжелее воды.
Данный металл тяжелее воды.
Данный металл – свинец.
5) Если небесное тело является планетой Солнечной системы, то оно движется вокруг Солнца.
Комета Галлея движется вокруг Солнца.
Комета Галлея является планетой Солнечной системы.
3.7. Условно-разделительный силлогизм
Первая посылка условно-разделительного силлогизма является условным (импликативным) суждением, а вторая посылка – разделительным (дизъюнктивным). Важно отметить, что в условном (импликативном) суждении может быть не одно основание и одно следствие (как в тех примерах, которые мы рассматривали до сих пор), а больше оснований или следствий. Например, в суждении: « Если поступать в МГУ, то надо много заниматься или же надо иметь много денег », – из одного основания вытекает два следствия, что с помощью условных обозначений можно представить в виде формулы: ( a → b ) ∧ ( a → c ). В суждении: « Если поступать в МГУ, то надо много заниматься, а если поступать в МГИМО, то тоже надо много заниматься », – из двух оснований вытекает одно следствие: ( a → b ) ∧ ( c → b ). В суждении: « Если страной правит мудрый человек, то она процветает, а если ею управляет проходимец, то она бедствует », – из двух оснований вытекает два следствия: ( a → b ) ∧ ( c → d ). В суждении: « Если я выступлю против окружающей меня несправедливости, то останусь человеком, хотя жестоко пострадаю; если равнодушно пройду мимо неё, то перестану себя уважать, хотя и буду цел и невредим; а если стану всячески содействовать ей, то превращусь в животное, хотя и достигну материального и карьерного благополучия », – из трёх оснований вытекает три следствия: ( a → b ) ∧ ( c → d ) ∧ ( e → f ).
Если в первой посылке условно-разделительного силлогизма содержится два основания или следствия, то такой силлогизм называется дилеммой , если оснований или следствий три, то он называется трилеммой , а если первая посылка включает в себя более трёх оснований или следствий, то силлогизм является полилеммой . Чаще всего в мышлении и речи встречается дилемма, на примере которой мы и рассмотрим условно-разделительный силлогизм (также часто называемый условно-разделительным умозаключением).
Дилемма может быть конструктивной (утверждающей) и деструктивной (отрицающей). Каждый из этих видов дилеммы, в свою очередь, делится на две разновидности: как конструктивная, так и деструктивная дилемма может быть простой и сложной.
В простой конструктивной дилемме из двух оснований вытекает одно следствие, вторая посылка представляет собой дизъюнкцию оснований, а в выводе утверждается это одно следствие в виде простого суждения. For example:
Если поступать в МГУ, то надо много заниматься, а если поступать в МГИМО, то тоже надо много заниматься.
Можно поступать в МГУ или МГИМО.
Надо много заниматься.
Форма модуса данной дилеммы:
((( a → b ) ∧ ( c → b )) ∧ ( a

c )) → b .
В первой посылке сложной конструктивной дилеммы из двух оснований вытекает два следствия, вторая посылка представляет собой дизъюнкцию оснований, а вывод является сложным суждением в виде дизъюнкции следствий. For example:
Если страной правит мудрый человек, то она процветает, а если ею управляет проходимец, то она бедствует.
Страной может управлять мудрый человек или проходимец.
Страна может процветать или бедствовать.
Форма модуса данной дилеммы:
((( a → b ) ∧ ( c → d )) ∧ ( a

c )) → ( b

d ).
В первой посылке простой деструктивной дилеммы из одного основания вытекает два следствия, вторая посылка представляет собой дизъюнкцию отрицаний следствий, а в выводе отрицается основание (происходит отрицание простого суждения). For example:
Если поступать в МГУ, то надо много заниматься или же надо много денег.
Я не хочу много заниматься или же тратить много денег.
Я не буду поступать в МГУ.
Форма модуса данной дилеммы:
((( a → b ) ∧ ( a → c )) ∧ (¬ b ∨ ¬ c )) → ¬ a .
В первой посылке сложной деструктивной дилеммы из двух оснований вытекают два следствия, вторая посылка представляет собой дизъюнкцию отрицаний следствий, а вывод является сложным суждением в виде дизъюнкции отрицаний оснований. For example:
Если философ считает первоначалом мира материю, то он материалист, а если он считает первоначалом мира сознание, то он идеалист.
Этот философ не материалист или не идеалист.
Этот философ не считает первоначалом мира материю, или он не считает первоначалом мира сознание.
Форма модуса данной дилеммы:
((( a → b ) ∧ ( c → d )) ∧ (¬ b

¬ d )) → (¬ a

¬ c ).
Поскольку первая посылка условно-разделительного силлогизма является импликацией, а вторая – дизъюнкцией, его правила – те же самые, что и рассмотренные выше правила условно-категорического и разделительно-категорического силлогизмов.
1. Что такое условно-разделительный силлогизм?
2. На каком основании выделяются такие разновидности условно-разделительного силлогизма, как дилемма, трилемма и полилемма?
3. Чем отличается конструктивная дилемма от деструктивной?
В чём заключается разница между простой конструктивной дилеммой и сложной? Придумайте по одному примеру для простой и сложной конструктивной дилеммы и выразите их форму с помощью условных логических обозначений.
4. Чем отличается простая деструктивная дилемма от сложной?
Придумайте по одному примеру для простой и сложной деструктивной дилеммы и выразите их форму с помощью условных логических обозначений.
5. Каковы правила условно-разделительного силлогизма?
3.8. Индуктивное умозаключение
В индукции из нескольких частных случаев выводится общее правило, рассуждение идёт от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы, как правило, вероятностны.
Индукция бывает полной и неполной. В полной индукции перечисляются все объекты из какой-либо группы и делается вывод обо всей этой группе. Например, если в посылках индуктивного умозаключения перечисляются все девять крупных планет Солнечной системы, то такая индукция является полной:
Меркурий движется. Венера движется. Земля движется. Марс движется… Плутон движется.
Меркурий, Венера, Земля, Марс, … Плутон – это крупные планеты Солнечной системы.
Все крупные планеты Солнечной системы движутся.
В неполной индукции перечисляются некоторые объекты из какой-либо группы и делается вывод обо всей этой группе. Например, если в посылках индуктивного умозаключения перечисляются не все девять крупных планет Солнечной системы, а только три из них, то такая индукция является неполной:
Меркурий движется. Венера движется. Земля движется. Меркурий, Венера, Земля – это крупные планеты Солнечной системы. Все крупные планеты Солнечной системы движутся.
Понятно, что выводы полной индукции достоверны, а неполной – вероятностны, однако полная индукция встречается редко, и поэтому под индуктивными умозаключениями обычно подразумевается неполная индукция.
Чтобы повысить степень вероятности выводов неполной индукции, следует соблюдать следующие важные правила:
1. Необходимо подбирать как можно больше исходных посылок . Для примера рассмотрим следующую ситуацию. Требуется проверить уровень успеваемости учащихся в некой школе. Предположим, что всего в ней учится (учитывая все классы и параллели) 1 000 человек. По методу полной индукции надо протестировать на предмет успеваемости каждого ученика из этой тысячи. Поскольку сделать это довольно сложно, можно использовать метод неполной индукции: протестировать какую-то часть учащихся и сделать общий вывод об уровне успеваемости в данной школе. Различные социологические опросы также базируются на применении неполной индукции. Очевидно, что чем большее число учеников подвергнется тестированию, тем более надёжной будет база для индуктивного обобщения, и более точным получится вывод. Однако просто большего числа исходных посылок, как того требует рассматриваемое правило, для повышения степени вероятности индуктивного обобщения недостаточно. Допустим, тестирование пройдёт немалое число учащихся, но, волей случая, среди них окажутся одни только неуспевающие. В этой ситуации мы придём к ложному индуктивному выводу о том, что уровень успеваемости в данной школе очень низок. Поэтому первое правило дополняется вторым.
2. Необходимо подбирать разнообразные посылки . Возвращаясь к нашему примеру, отметим, что множество тестируемых должно быть не просто по возможности большим, но и специально, по системе, сформированным, а не случайно подобранным, т. е. надо позаботиться о том, чтобы в него вошли учащиеся (примерно в одинаковом количественном отношении) из разных классов, параллелей и т. п. И, наконец, третье правило неполной индукции предписывает следующее.
3. Необходимо делать вывод только на основе существенных признаков . Если, допустим, во время тестирования выясняется, что ученик 10 класса не знает наизусть всю периодическую систему химических элементов, то этот факт (признак) является несущественным для вывода о его успеваемости. Однако, если тестирование показывает, что ученик 10 класса частицу «не» с глаголом пишет слитно, то этот факт (признак) следует признать существенным (важным) для вывода об уровне его образованности и успеваемости.
Таковы основные правила неполной индукции. Теперь обратимся к её наиболее распространённым ошибкам. Говоря о дедуктивных умозаключениях, мы рассматривали ту или иную ошибку вместе с правилом, нарушение которого её порождает. В данном случае сначала представлены правила неполной индукции, а потом, отдельно, – её ошибки. Это объясняется тем, что каждая из них не связана непосредственно с каким-то из вышеприведённых правил. Любую индуктивную ошибку можно рассматривать как результат одновременного нарушения всех правил, и в то же время нарушение каждого правила можно представить как причину, приводящую к любой из ошибок.
Первая ошибка, часто встречающаяся в неполной индукции, называется поспешным обобщением . Скорее всего, каждый из нас, хорошо с ней знаком. Всем приходилось слышать такие высказывания: «Все мужчины чёрствые», «Все женщины легкомысленные» .
Эти расхожие стереотипные фразы представляют собой не что иное, как поспешное обобщение в неполной индукции: если некоторые объекты из какой-либо группы обладают неким признаком, то это вовсе не означает, что данным признаком характеризуется вся группа без исключения. Из истинных посылок индуктивного умозаключения может вытекать ложный вывод, если допустить поспешное обобщение. For example:
К. учится плохо. Н. учится плохо. С. учится плохо.
К., Н., С. – это ученики 10 «А».
Все ученики 10 «А» учатся плохо.
Неудивительно, что поспешное обобщение лежит в основе многих голословных утверждений, слухов и сплетен.
Вторая ошибка носит длинное и, на первый взгляд, странное название: после этого, значит по причине этого (от лат. post hoc, ergo propter hoc ). В данном случае речь идёт о том, что если одно событие происходит после другого, то это не означает с необходимостью их причинно-следственную связь. Два события могут быть связаны всего лишь временной последовательностью (одно – раньше, другое – позже). Когда мы говорим, что одно событие обязательно является причиной другого, потому что одно из них произошло раньше другого, то допускаем логическую ошибку. Например, в следующем индуктивном умозаключении обобщающий вывод является ложным, несмотря на истинность посылок:
Позавчера двоечнику Н. перебежала дорогу чёрная кошка, и он получил двойку. Вчера двоечнику Н. перебежала дорогу чёрная кошка, и его родителей вызвали в школу. Сегодня двоечнику Н. перебежала дорогу чёрная кошка, и его исключили из школы.
Во всех несчастьях двоечника Н. виновата чёрная кошка.
Из-за ошибки «после этого, значит по причине этого» рождаются небылицы, суеверия и мистификации.
Третья ошибка, широко распространённая в неполной индукции, называется подмена условного безусловным . Рассмотрим индуктивное умозаключение, в котором из истинных посылок вытекает ложный вывод:
Дома вода кипит при температуре 100 °C. На улице вода кипит при температуре 100 °C. В лаборатории вода кипит при температуре 100 °C. Вода везде кипит при температуре 100 °C.
Мы знаем, что высоко в горах вода кипит при более низкой температуре. То, что проявляется в одних условиях, может не проявляться в других. В посылках рассмотренного примера присутствует условное (происходящее в определённых условиях), которое подменяется безусловным (происходящим во всех условиях одинаково, не зависящим от них) в выводе. Хороший пример подмены условного безусловным содержится в известной нам с детства сказке про вершки и корешки, в которой речь идёт о том, как мужик и медведь посадили репу, договорившись поделить урожай следующим образом: мужику – корешки, медведю – вершки. Получив ботву от репы, медведь понял, что мужик его обманул, и совершил логическую ошибку подмены условного безусловным: надо всегда брать только корешки, – решил он. На следующий год, когда мужик и медведь делили урожай пшеницы, медведь сам предложил, что он возьмёт корешки, а мужик – вершки, и опять остался ни с чем.
Неполная индукция бывает популярной и научной. В популярной индукции вывод делается на основе наблюдения и простого перечисления фактов, без знания их причины, а в научной индукции вывод делается не только на основе наблюдения и перечисления фактов, но ещё и на основе знания их причины. Поэтому научная индукция, в отличие от популярной, характеризуется намного более точными, почти достоверными выводами. Например, первобытные люди видят, как солнце каждый день встаёт на востоке, медленно движется в течение дня по небу и закатывается на западе, но они не знают, почему так происходит, им неизвестна причина этого постоянно наблюдаемого явления. Понятно, что они могут сделать умозаключение, используя только популярную индукцию и рассуждая примерно следующим образом: « Позавчера солнце взошло на востоке, вчера солнце взошло на востоке, сегодня солнце взошло на востоке, следовательно, солнце всегда всходит на востоке ». Мы, как и первобытные люди, наблюдаем каждодневный восход солнца на востоке, но, в отличие от них, знаем причину этого явления: Земля вращается вокруг своей оси в одном и том же направлении с неизменной скоростью, в силу чего солнце появляется каждое утро в восточной стороне неба. Поэтому то умозаключение, которое делаем мы, представляет собой научную индукцию и выглядит примерно так: « Позавчера солнце взошло на востоке, вчера солнце взошло на востоке, сегодня солнце взошло на востоке; причём это происходит оттого, что уже несколько миллиардов лет Земля вращается вокруг своей оси и будет вращаться так же и дальше в течение многих миллиардов лет, находясь на одном и том же расстоянии от Солнца, которое родилось раньше Земли и будет существовать дольше неё; следовательно, Солнце, для земного наблюдателя всегда всходило и будет всходить на востоке ».
Главное отличие научной индукции от популярной заключается в знании причин происходящих событий. Поэтому одна из важных задач не только научного, но и повседневного мышления – это обнаружение причинных связей и зависимостей в окружающем нас мире.
1. Что такое индуктивное умозаключение? Чем оно отличается от дедуктивного?
2. В чём разница между полной и неполной индукцией? Придумайте один пример для полной индукции и один – для неполной.
Почему под индукцией, как правило, подразумевается неполная индукция?
3. Каковы основные правила неполной индукции? Приведите в качестве примера какую-нибудь ситуацию (за исключением той, которая была рассмотрена в параграфе) и покажите с её помощью, как соблюдение основных правил неполной индукции способствует повышению степени вероятности индуктивных обобщений.
4. Каковы основные ошибки, широко распространённые в неполной индукции? К каким негативным явлениям в духовной жизни человека и общества они могут привести? Придумайте по одному примеру для каждой ошибки в неполной индукции.
5. Чем отличается популярная индукция от научной? Приведите по одному примеру (за исключением тех, которые были представлены в параграфе) для популярной и научной индукции.
3.9. Установление причинной зависимости
В логике рассматриваются четыре метода установления причинных связей. Впервые их выдвинул английский философ XVII в. Фрэнсис Бэкон, а всесторонне разработаны они были английским логиком и философом XIX в. Джоном Стюартом Миллем.
Метод единственного сходства строится по следующей схеме:
При условиях ABC возникает явление x. При условиях ADE возникает явление x. При условиях AFG возникает явление x.
Вероятно, условие A – это причина явления x.
Перед нами – три ситуации, в которых действуют условия A, B, C, D, E, F, G , причём одно из них ( A ) повторяется в каждой. Это повторяющееся условие – единственное, в чём схожи между собой данные ситуации. Далее, надо обратить внимание на то, что во всех ситуациях возникает явление x . Из этого можно сделать вероятный вывод, что условие A представляет собой причину явления x (одно из условий всё время повторяется, и явление при этом постоянно возникает, что и даёт основание объединить первое и второе причинно-следственной связью). Например, требуется установить, какой продукт питания вызывает у человека аллергию. Допустим, в течение трёх дней аллергическая реакция неизменно возникала. При этом в первый день человек употреблял в пищу продукты A, B, C , во второй день – продукты A, D, E , в третий день – продукты A, F, G , т. е. на протяжении трёх дней повторно принимался в пищу только продукт A , который, скорее всего, и является причиной аллергии.
Метод единственного различия строится таким образом:
При условиях ABCD возникает явление x.
При условиях BCD не возникает явление x.
Вероятно, условие A – это причина явления x.
Как видим, две ситуации различаются между собой только в одном: в первой условие A присутствует, а во второй оно отсутствует.
Причём в первой ситуации явление x возникает, а во второй – не возникает. На основании этого можно предположить, что условие A и есть причина явления x . Например, в воздушной среде металлический шарик падает на землю раньше, чем пёрышко, брошенное одновременно с ним с той же высоты, т. е. шарик движется к земле с большим ускорением, чем пёрышко. Однако, если проделать данный эксперимент в безвоздушной среде (все условия – те же самые, кроме наличия воздуха), то и шарик, и пёрышко будут падать на землю одновременно, т. е. с одинаковым ускорением. Видя, что в воздушной среде различное ускорение падающих тел имеет место, а в безвоздушной, – не имеет, можно заключить, что, по всей вероятности, сопротивление воздуха является причиной падения разных тел с различным ускорением.
Метод сопутствующих изменений построен так :
При условиях A BCD возникает явление x . 1 1 При условиях A BCD возникает явление x . 2 2 При условиях A BCD возникает явление x . п 3 3 Вероятно, условие A – это причина явления x.
Изменение одного из условий (при неизменности прочих условий) сопровождается изменением происходящего явления, в силу чего можно утверждать, что данное условие и указанное явление объединены причинно-следственной связью. Например, при увеличении скорости движения в два раза пройденный путь увеличивается также вдвое; если скорость возрастает в три раза, то и пройденное расстояние становится в три раза большим. Следовательно, увеличение скорости является причиной увеличения пройденного пути (разумеется, за один и тот же промежуток времени).
Метод остатков строится следующим образом:
При условиях ABC возникает явление xyz. Известно, что часть у изъявления xyz вызывается условием B. Известно, что часть z изъявления xyz вызывается условием C. Вероятно, условие A – это причина явления x.
В данном случае происходящее явление разбито на составные части и известна причинная связь каждой из них, кроме одной, с каким-либо условием. Если остаётся только одна часть из возникающего явления и только одно условие из совокупности условий, порождающих это явление, то можно утверждать, что оставшееся условие представляет собой причину оставшейся части рассмотренного явления. Например, рукопись автора читали редакторы A., B., C. , делая в ней пометки шариковыми авторучками. Причём известно, что редактор B. правил рукопись синими чернилами ( у ), а редактор C. – красными ( z ). Однако в рукописи имеются пометки, сделанные зелёными чернилами ( x ). Можно заключить, что, скорее всего, они оставлены редактором A .
1. Что представляет собой метод единственного сходства? Придумайте какой-нибудь пример использования этого метода.
2. По какой схеме строится метод единственного различия? Придумайте какой-нибудь пример использования этого метода.
3. Каким образом устанавливается причинная связь с помощью метода сопутствующих изменений? Придумайте какой-нибудь пример использования этого метода.
4. Как обнаруживаются причины происходящих явлений с помощью метода остатков? Придумайте какой-нибудь пример использования этого метода.
5. Как обычно применяются методы установления причинных связей в научном и повседневном мышлении? Подумайте, почему выводы, получаемые с помощью этих методов, остаются в большей или меньшей степени вероятными?
6. Определите, с помощью каких методов установления причинных связей получены выводы в следующих ситуациях:
1) Наблюдая за движением планеты Уран, астрономы XIX в. заметили, что она несколько отклоняется от своей орбиты. Было установлено, что Уран отклоняется на величины a, b, c, причём эти отклонения вызваны влиянием соседних планет A, B, C. Однако также было замечено, что Уран в своём движении отклоняется не только на величины a, b, c, но ещё и на величину d. Из этого сделали предположительный вывод о наличии за орбитой Урана пока неизвестной планеты, которая вызывает данное отклонение. Французский учёный Урбен Жан Жозеср Леверье рассчитал положение этой планеты, а немецкий учёный Иоганн Готфрид Галле с помощью сконструированного им телескопа нашёл её на небесной сфере. Так в XIX в. была открыта планета Нептун.
2) Листья растения, которое выросло в подвале, не имеют зелёной окраски. Листья того же растения, выросшего в обычных условиях, – зелёные. В подвале нет света. В обычных условиях растение произрастает на солнечном свету. Следовательно, он является причиной возникновения зелёного цвета растений.
3) Ещё в древности было замечено, что периодичность морских приливов и изменение их высоты соответствует изменениям в положении Луны. Наибольшие приливы приходятся на дни новолуний и полнолуний, наименьшие – на так называемые дни квадратур (когда направления от Земли к Луне и Солнцу образуют прямой угол). На основании этих наблюдений был сделан вывод о том, что морские приливы обусловливаются действием Луны.
4) Исследовалось влияние небольших доз алкоголя на точность стрельбы из винтовки на 250 м, лёжа, десятью патронами, без ограничения времени. Когда стрелки были трезвыми, 86 % пуль поразило мишени, а 14 % пуль попало в щиты. После употребления алкоголя в мишени было послано 20 % пуль, в щиты – 34 %, а 46 % пуль не попало даже в щиты. Следовательно, употребление алкоголя является причиной снижения точности стрельбы.
3.10. Виды и правила аналогии
В умозаключениях по аналогии на основе сходства предметов в одних признаках делается вывод об их сходстве и в других признаках. Структура аналогии может быть представлена следующей схемой:
Предмет A имеет признаки a, b, c, d.
Предмет B имеет признаки a, b, c.
Вероятно, предмет B имеет признак d.
В ней A и B – это сравниваемые или уподобляемые друг другу предметы (объекты); a, b, c – сходные признаки; d – это переносимый признак. Приведём пример умозаключения по аналогии:
Сочинения философа Секста Эмпирика, выпущенные издательством «Мысль» в серии «Философское наследие», снабжены вступительной статьёй, комментариями и предметно-именным указателем.
В аннотации к книжной новинке – сочинениям философа Фрэнсиса Бэкона – говорится, что они выпущены издательством «Мысль» в серии «Философское наследие», и снабжены вступительной статьёй и комментариями.
Скорее всего, выпущенные сочинения Фрэнсиса Бэкона так же, как и сочинения Секста Эмпирика, снабжены предметно-именным указателем.
In this case, two objects are compared (matched): the previously published works of Sextus Empiricus and the published works of Francis Bacon. Similar signs of these two books are that they are published by the same publisher, in the same series, with introductory articles and commentaries. Based on this, with a high degree of probability, it can be argued that if the works of Sextus Empiricus are provided with a subject-name index, then the works of Francis Bacon will be equipped with them. Thus, the presence of a subject-nominal index is a portable attribute in the considered example (see also paragraph 3.1., Where the planets Earth and Mars act as assimilated objects, and the portable attribute is the presence on the planet of life).
Inference by analogy is divided into two types:
1. Analogy of properties , in which two objects are compared, and a portable attribute is any property of these objects.
The above example is an analogy of properties.
2. Analogy of relations , in which two groups of objects are compared, and a portable attribute is any relation between objects within these groups. An example of the analogy of relationships:
In a mathematical fraction, the numerator and denominator are in inverse relationship: the greater the denominator, the smaller the numerator. A person can be compared with a mathematical fraction: the numerator is what it really is, and the denominator is what he thinks of himself, how he evaluates himself. It is likely that the higher a person evaluates himself, the worse he actually becomes.
As you can see, two groups of objects are compared. One is the numerator and denominator in a mathematical fraction, and the other is a real person and his self-esteem. Moreover, the inverse relationship between objects is transferred from the first group to the second.
By virtue of the probabilistic nature of their conclusions, the analogy, of course, is closer to induction than to deduction. It is not surprising, therefore, that the basic rules of analogy, the observance of which makes it possible to increase the degree of probability of its conclusions, in many ways resemble the rules of incomplete induction already known to us. First, it is necessary to draw a conclusion on the basis of the greatest possible number of similar signs in the similar objects. Secondly, these signs should be diverse. Thirdly, similar signs should be essential for the objects being compared.
Fourthly, between the similar signs and the portable sign there must be a necessary (regular) connection. The first three analogy rules actually repeat the rules of incomplete induction. Perhaps the most important is the fourth rule about the connection of similar traits and portable trait. Let us return to the example of the analogy considered at the beginning of this section. A portable attribute — the presence of a subject-name index in a book — is closely related to similar features — a publishing house, a series, an introductory article, and comments (books of this genre must be supplied with a subject-name index). If the transferred attribute (for example, the volume of the book) is not naturally associated with similar signs, then the conclusion by analogy may turn out to be false:
The writings of the philosopher Sextus Empiricus, published by Thought in the Philosophical Heritage series, are provided with an introductory article, comments, and have a volume of 590 pages.
In the annotation to the book novelty - the writings of the philosopher Francis Bacon - states that they were released by the publishing house "Thought" in the series "Philosophical Heritage", and are provided with an introductory article and comments.
Most likely, the released works of Francis Bacon, as well as the works of Sextus Empiricus, have a volume of 590 pages.
Despite the probabilistic nature of the conclusions, inference by analogy has many merits. Analogy is a good means of illustrating and explaining some complex material; it is a way of giving it artistic imagery, often leading to scientific and technical discoveries.
1. What is the structure of conclusions by analogy?
2. How does the analogy of properties differ from the analogy of relations?
Give one example (with the exception of those discussed in the paragraph) for each of these types of analogy.
3. What are the basic rules of reasoning by analogy, the observance of which allows to increase the degree of probability of its conclusions?
4. What are the advantages and disadvantages of inferences by analogy?
5. Determine the type of analogy in the examples below:
1) Gills for fish is the same as lungs for mammals .
2) Arthur Conan Doyle's story The Sign of Four about the adventures of the detective Sherlock Holmes, distinguished by a dynamic plot, I really liked. I did not read Arthur Conan Doyle's novel The Hound of the Baskervilles, but I know that it is dedicated to the adventures of the noble detective Sherlock Holmes and has a dynamic plot. Most likely, I also really like this story.
3) The essence of the planetary model of Ernest Rutherford's atom is that in it around the positively charged nucleus negative electrons move in different orbits; just as in the Solar System, the planets move in different orbits around a single center - the Sun.
Comments
To leave a comment
Logics
Terms: Logics