2.3. Distributed and unallocated terms

Terms of judgment are his subject and predicate.

A term is considered to be distributed (expanded, exhausted, taken in its entirety), if the judgment refers to all objects included in the scope of this term. The distributed term is denoted by the “+” sign, and in the schemes of Euler it is depicted as a full circle (a circle that does not contain another circle and does not intersect with another circle) (Fig. 22).

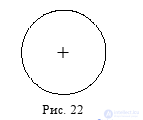
A term is considered to be unallocated (undeployed, inexhaustible, not fully taken), if the judgment does not refer to all objects included in the scope of this term. The unassigned term is indicated by the sign “-”, and in the schemes of Euler it is depicted as an incomplete circle (a circle that contains another circle (Fig. 23a ) or intersects with another circle (Fig. 23b ).

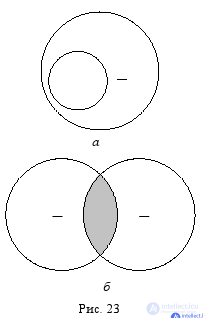
Например, в суждении: « Все акулы (S) являются хищниками (Р) », – речь идёт обо всех акулах, значит, субъект этого суждения распределён.

Однако в данном суждении речь идёт не обо всех хищниках, а только о части хищников (именно о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределён. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения схемами Эйлера, увидим, что распределённому термину (субъекту « акулы ») соответствует полный круг, а нераспределённому (предикату « хищники ») – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть):

The distribution of terms in simple judgments can vary depending on the type of judgment and the nature of the relationship between its subject and predicate. In tab. 4 shows all cases of distribution of terms in simple judgments:

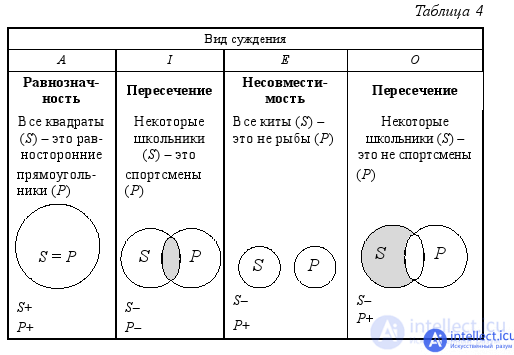
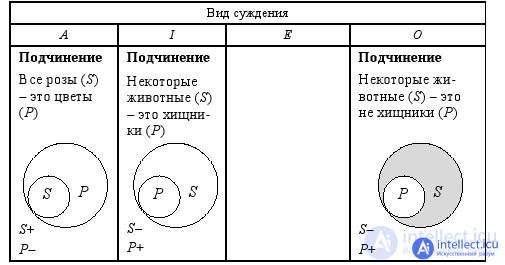
Here we consider all four types of simple judgments and all possible cases of relations between the subject and the predicate in them (see section 2. 2). Note the judgments of the form O , in which the subject and the predicate are in relation to the intersection. Despite intersecting circles in the Euler scheme, the subject of this judgment is unallocated and the predicate is distributed. Why is this so? Выше мы говорили о том, что пересекающиеся на схеме круги Эйлера обозначают нераспределённые термины. Штриховкой показана та часть субъекта, о которой идёт речь в суждении (в данном случае – о школьниках, которые спортсменами не являются), в силу чего круг, обозначающий на схеме Эйлера предикат, остался полным (круг, обозначающий субъект, не отрезает от него какую-то часть, как это происходит в суждении вида I , где субъект и предикат находятся в отношении пересечения).

Итак, мы видим, что субъект всегда распределён в суждениях вида A и E и всегда не распределён в суждениях вида I и O , а предикат всегда распределён в суждениях вида E и O , но в суждениях вида A и I он может быть как распределённым, так и нераспределённым в зависимости от характера отношений между ним и субъектом в этих суждениях.

It is easiest to establish the distribution of terms in simple judgments using Euler schemes (it is not necessary to remember all cases of distribution from the table). It is enough to be able to determine the type of relationship between the subject and the predicate in the proposed judgment and depict them in circular patterns. Further, it is even simpler - a full circle, as already mentioned, corresponds to a distributed term, and an incomplete one to an unallocated one. For example, it is required to establish the distribution of terms in the judgment: " Some Russian writers are world-famous people ." First we find in this proposition a subject and a predicate: “ Russian writers ” is a subject, “ world famous people » – предикат. Теперь установим, в каком они отношении. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 25):

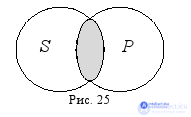
И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены ( S –, P –).

Рассмотрим ещё один пример. Надо установить распределённость терминов в суждении: « Некоторые люди – это спортсмены ». Найдя в этом суждении субъект и предикат: « люди » – субъект, « спортсмены » – предикат, и установив отношение между ними – подчинение, изобразим его на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 26):

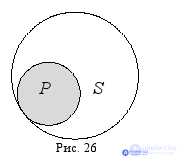
Круг, обозначающий предикат, является полным, а круг, соответствующий субъекту, – неполным (круг предиката как бы вырезает из него какую-то часть). Таким образом, в данном суждении субъект нераспределён, а предикат распределён ( S –, P –).

Check yourself:

1. В каком случае термин суждения считается распределённым, а в каком – нераспределённым? Как с помощью круговых схем Эйлера можно установить распределённость терминов в простом суждении?

2. Какова распределённость терминов во всех видах простых суждений и во всех случаях отношений между их субъектом и предикатом?

3. С помощью схем Эйлера установите распределённость терминов в следующих суждениях:

1) Все насекомые являются живыми организмами.

2) Некоторые книги – это учебники.

3) Некоторые учащиеся не являются успевающими.

4) Все города – это населённые пункты.

5) Ни одна рыба не является млекопитающим.

6) Некоторые древние греки являются знаменитыми учёными.

7) Некоторые небесные тела – это звёзды.

8) Все ромбы с прямыми углами – это квадраты.

See also

• 3.4 Judgments in logic. Judgment as a form of thinking.
• 2.2. Simple judgments
• 2.3. Distributed and unallocated terms
• 2.4. Transforming a Simple Judgment
• 2.5. Logical square. Comparable and incomparable judgments
• 2.6. Complicated judgment, composition and classification, truth rules
• 2.7. Logical formulas