Lecture
1.5. Definition operation
The definition of a concept is a logical operation that reveals the content of the concept.
Definitions are explicit and implicit.
Explicit definition directly reveals the content of the concept, gives a direct answer to the question, what is the object that it denotes. For example: “A thermometer is a physical device designed to measure temperature, ” is an explicit definition.
The implicit (contextual) definition reveals the content of the concept not directly, but indirectly, using the context in which this concept is used. For example, from the following phrase: “ During this grand experiment, ultra-precise thermometers recorded a temperature of 1,000 ° C ,” indirectly follows the answer to the question: “What is a thermometer?” - an implicit definition of this concept follows. It is clear that definitions in the full sense of the word should be considered explicit definitions. In the future, it will be about them.
Definitions are also real and nominal.
The real definition reveals the content of the concept denoting an object, that is, they are devoted to objects. For example:
“A thermometer is a physical device designed to measure temperature ” is the real definition.
The nominal (from Lat. Nomen - name) reveals the meaning of a term by which a concept is expressed, i.e. they are devoted to terms (words). For example: " The word" thermometer "means a physical device for measuring temperature, " is the nominal definition.
As we see, there is no fundamental difference between real and nominal definitions. They differ, as a rule, in a form, but not in essence.
There are several ways to define a concept, but the classical method stands out among them, which consists in the fact that the concept being defined is brought under the closest generic concept, followed by an indication of its species difference. For example, the definition: “ Astronomy is the science of celestial bodies ” is built according to the classical method. It defines the concept of “ astronomy ” firstly under the closest generic concept of “ science ” (astronomy is necessarily science, but science is not necessarily astronomy), and then it points to the specific difference of astronomy from other sciences: “... about celestial bodies ". Using the classical method, you will be able to give an exact and correct definition to any concept, of course, if you define the object or term well, and you know what it is or what it means, respectively. For example, we need to define the concept of " square ". Following the classical method, we first sum it up under the generic concept: “A square is a geometric figure ,” and then we will point out its specific difference from other geometric figures, which consists in the presence of equal sides and right angles . So: "A square is a geometric figure, in which all sides are equal and the corners are straight ." Giving a definition of the concept of " square ", we could bring it under the more generic concept of " rectangle ", and then the definition would be the following: "A square is a rectangle with all sides equal " - however, the above definition of a square reveals the contents corresponding concept and is true. Note that virtually all definitions found in the scientific, educational and reference literature, for example in the explanatory dictionaries, are built according to the classical method.
There are several logical rules for determining. Violation of at least one of them leads to the fact that the content of the concept is not disclosed and the definition does not reach its goal, being incorrect. Consider these rules and errors that occur when they are violated:
1. The definition should not be broad , i.e. the definition should not exceed in its scope the defined concept. For example, the definition: “The sun is a celestial body ” is broad : the definition of “ celestial body ” is much larger in terms of the definition of the term “ Sun ”. From the above definition, it is not quite clear what the Sun is, because the celestial body is both a planet, and a comet, etc. In this case, we can also say that, using the classical method of definition, we have put the defined concept " Sun " under the generic concept " Heavenly body ", but did not make the second step - did not indicate its specific difference.
2. The definition should not be narrow , i.e. the definition should not be less than the defined concept in its scope. For example, the definition: “ Geometry is the science of triangles ,” is narrow . Geometry is really the science of triangles, but not only about them, but in our example the definition turned out to be less than the defined concept by volume, as a result of which the definition is not quite clear what geometry is, the content of the concept is not disclosed.
As we see, the narrow definition error is the opposite of the wide definition error. If the definition should not be broad and not narrow, then how should it be? It must be proportionate, that is, the concept and its definition must be equal to each other. Let us return to the definition: “ Astronomy is the science of celestial bodies ” - which is proportionate. In this example, the defined concept of " astronomy " and the definition: "... the science of celestial bodies " are in relation to equivalence: astronomy is the science of celestial bodies, and the science of celestial bodies is only astronomy. The definition is proportional when between its first part (defined by the concept) and the second (definition), you can put the sign "=". If the sign “>” or “<” is put between the first and the second part of the definition, then it is erroneous - wide or narrow, respectively. In this case, we see a manifestation of one of the basic laws of logic - the law of identity.
3. In the definition there should not be a circle , i.e. in the definition it is impossible to use concepts that are definable. For example, in the definition: “The slanderer is a person who engages in slander ,” a circle is present, since the concept of slanderer is defined through the concept of slander , that is, in fact, through itself. If, having heard the above definition, we asked what slander is, we could be answered: “ Slander is what the slanderer does .” The circle present in the definition (or tautology, from Greek. - repetition) leads to the fact that the content of the concept is not disclosed, and the definition is erroneous. However, there will surely be people who say that from the definition: “A slanderer is a person who engages in slander ”, is quite understandable, and who such a slanderer is, and what is slander. They can only say this because they previously knew the meaning of the words " slanderer " and " slander ." Will it be clear what existentialism is from the following circular definition: “ Existentialism is the philosophical direction of the 20th century, in which various existential questions and problems are posed and comprehensively addressed ”? Do we know what synergetics is due to such a circular definition: “ Synergetics is a branch of modern natural science that studies various synergistic phenomena and processes ”?
4. The definition should not be ambiguous , that is, it cannot use words (terms) in a figurative sense. Let us recall the definition well known from childhood: “The lion is the king of beasts ”. In this definition, the word " king " is used in a figurative sense, but it also has a direct meaning. It turns out that the definition uses one word, and it has two possible values, that is, the definition is ambiguous (the logical law of identity is again violated: one word, two values: 1 2).
Ambiguity is quite appropriate as an artistic device, but in the definition it is unacceptable, since the content of the concept is not disclosed in this case.
5. The definition should not be complicated and incomprehensible .
Consider the following definition: " Entropy is a thermodynamic function that characterizes a part of the internal energy of a closed system that cannot be converted into mechanical work ." This definition was taken not from a scientific report or from a doctoral dissertation, but from a textbook for students of humanitarian specialties [2] . This definition is not broad and not narrow, it does not have a circle and ambiguity, it is also true from a scientific point of view. This definition seems flawless, with the only exception that it is difficult and incomprehensible for people who are not specifically engaged in the natural sciences, that is, for most of us. The definition should be clear for the one to whom it is addressed, otherwise, for all its formal correctness, it will not reveal the content of the concept to its addressee. Incomprehensible definitions are also called uncommunicative , that is, they create barriers to communication between people.
6. The definition should not be only negative . For example, the definition: “A square is not a triangle ” is only negative . A square is really not a triangle, but this definition does not disclose the content of the concept of “ square ”, because, pointing out what the object is not, the designated concept is not, we did not say what it is (circle, trapezium, pentagon is also not squares). The definition may be negative in the case when it is supplemented by a positive part. For example, the definition: “A square is not a triangle, but a rectangle, in which all sides are equal, ” is correct.
1. What is the definition of a concept?
2. What is the difference between explicit definitions and implicit ones? Come up with three examples of explicit and implicit definitions.
3. What are real and nominal definitions? Why do you think any real definition can be reduced to nominal and vice versa?
4. What is the classic way to define a concept? Give the definition of any three concepts, using the classical method.
5. What are the basic rules for defining a concept? What mistakes occur when they are violated? Give, having picked up, three examples for each error in the definition of the concept.
6. Find the errors in the definition examples below:
1) Day is the length of time during which the Earth makes a complete revolution around its axis .
2) A genre is a stable form of a work of art .
3) A dog is a friend of man .
4) Creative thinking is thinking that provides a solution to creative problems .
5) The revolution is a major historical event, as a result of which political power is changing in society .
1.6. Division operation
The division of a concept is a logical operation that reveals its scope.
The division of a concept consists of three parts: the dividend concept, the results of the division, the basis of the division (the sign on which the division is made). For example, in the following division: “ People are men and women ,” or, which is the same: “ People are divided into men and women, ” the concept of “ people ” is divisible, the results of the division are the concepts of “ man ” and “ woman ", And the basis of this division is gender, because people in it are divided by gender. Depending on the base, the division may be different. For example: " People are high, low and medium height (the basis of division is growth)", " People are Mongoloids, Caucasians and Negroids (basis of division is race)", " People are teachers, doctors, engineers, etc. (basis division - a profession) ". Sometimes the concept is divided dichotomously (from the Greek. - in half) according to the type: "A and not A". For example: " People are athletes and not athletes ." Dichotomic division is always correct, that is, it automatically excludes all possible errors in division, which will be discussed below.
We know well why we need a definition operation: acquaintance with a new subject begins with its definition. Now let's answer the question what role in thinking and language does the operation of dividing the concept. Studying different sciences, you noticed that none of them can do without different classifications: divisions of some areas of reality into groups, parts, species, etc. (classification of plants in botany, animals in zoology, chemical elements in chemistry, etc.). However, any classification is nothing but a logical division operation of a concept. Classifications can be both extensive, detailed, scientific, and simple, everyday, everyday. When we say: “ People are divided into men and women ” or “ Educational institutions are elementary, secondary and higher ”, then we create a small and simple, but classification. So, the logical operation of dividing a concept lies at the heart of any classification, without which neither scientific nor everyday thinking can do.
There are several logical rules of division. Violation of at least one of them leads to the fact that the volume of the concept is not disclosed and the division does not reach its goal, being incorrect. Consider these rules and errors that occur when they are violated:
1. The division should be carried out on one basis , that is, when dividing the concept, only one selected attribute should be followed. For example, in the division: “ People are men, women and teachers ” - two different bases are used: gender and profession, which is unacceptable. The error arising from the violation of this rule is called the substitution of the base .
In the division with the substitution of the base can be used not only two different bases, as in the example above, but more. For example, in the division: “ People are men, women, Chinese, and blondes, ” three different bases were used: gender, nationality, and hair color, which, of course, is also a mistake.
2. The division must be complete , that is, it is necessary to list all possible division results: the total volume of all division results must be equal to the volume of the original dividend concept.
For example, the division: “ Educational institutions are primary and secondary ,” is incomplete , since one more result of the division is not indicated - “ higher education institutions ”. But what if you need to list not two or three, but tens or hundreds of division results.
In this case, you can use the following concepts: and others, and others, and so on and so forth , which will include not listed results of division. For example: " People are Russian, German, Chinese, Japanese, and other nationalities ."
3. The results of division should not overlap , that is, concepts representing the results of division should be incompatible, their volumes should not have common elements (in the Euler scheme, circles indicating the results of division should not touch). For example, in the division: "The countries of the world are divided into northern, southern, eastern and western, " an error was made - the intersection of the results of division . At first glance, the above division seems to be unmistakable: it is carried out on one base (side of the world) and is complete (all sides of the world are listed). To see the error, you need to reason like this. Take a country, for example Canada, and answer the question whether it is northern. Of course, it is, because it is located in the northern hemisphere of the Earth. Is Canada a western country?
Yes, because it is located in the western hemisphere. Thus, it turns out that Canada is both a northern and a western country, i.e. it is a common element in the scope of the notions “ northern countries ” (C) and “ western countries ” (W), which means these concepts intersect. The same can be said about the concepts of " southern countries " (S) and " eastern countries " (B). In the Euler scheme, the division results from our example will be arranged as follows (Fig. 15):

Recall that each classification is structured in such a way that any element that falls into one of its groups (part, species) does not fall into the others in any way. This is the result of non-intersection of the results of division (their mutual exclusion).
4. The division should be consistent , i.e., not allowing gaps and jumps. Consider the following division: " Forests are coniferous, deciduous, mixed and pine ." Clearly superfluous here is the notion of “ pine forests ”, by virtue of which the mistake made in the division resembles the substitution of the base (see the first rule). However, the basis in this case did not change: the division was carried out on the same basis - the type of woody leaves. The substitution of the base is present in this, for example, division: “ Forests are coniferous, deciduous, mixed, near Moscow and taiga .” The division was carried out on two different bases: the type of woody leaves and the geographical location of the forest. Let's return to our first example. It would be correct to divide the forests into coniferous, deciduous and mixed, and then make a second division - to divide the coniferous forests into pine and spruce. Таким образом, надо было совершить два последовательных деления, а в приведённом примере второе деление пропущено, через него как бы перескочили, в результате чего два деления смешались в одно. Такая ошибка называется скачком в делении . Ещё раз отметим, что скачок в делении не следует путать с подменой основания. Например, в делении: « Учебные заведения бывают начальными, средними, высшими и университетами », – присутствует скачок, а в делении: « Учебные заведения бывают начальными, средними, высшими и коммерческими », – допущена подмена основания.
1. Что такое деление понятия?
2. Какова структура деления? Что такое основание деления?
3. Какое деление называется дихотомическим? Попробуйте отметить достоинства и недостатки дихотомического деления.
4. What is the role of logical division operations in scientific and everyday thinking?
5. What are the basic logical rules for dividing a concept? What mistakes arise when they are violated? Think of three examples for each mistake in the division of the concept.
6. Why is the dichotomous division of a concept always unmistakable?
How does it eliminate all possible division errors?
7. Find errors in the following examples of division:
1) Transport is land, underground, water, air, public and personal .
2) By temperament, people are divided into sanguine, melancholic, phlegmatic and choleric .
3) Geometric shapes are divided into flat, three-dimensional, triangles and squares .
4) Отбор в живой природе бывает искусственным или естественным .
5) Художественные романы бывают приключенческими, детективными, фантастическими, историческими, любовными и другими .
1.7. Логическая сумма и логическое произведение
Сложение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объёмом, охватывающим собой все элементы объёмов исходных понятий. Например, при сложении понятий « школьник » (Ш) и « спортсмен » (С) образуется новое понятие, в объём которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой , на схеме Эйлера изображается штриховкой (рис. 16).

Умножение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объёмом, охватывающим собой только совпадающие элементы объёмов исходных понятий. Например, при умножении понятий « школьник » (Ш) и « спортсмен » (С) образуется новое понятие, в объём которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением , на схеме Эйлера изображается штриховкой (так же, как и результат сложения) (рис. 17).
Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения: « школьник » и « спортсмен ».
In other respects between the concepts of the results of addition and multiplication (logical sum and logical product), of course, will be different. In the table below. 3, the shading shows the results of the addition and multiplication of concepts in all kinds of relations between them.
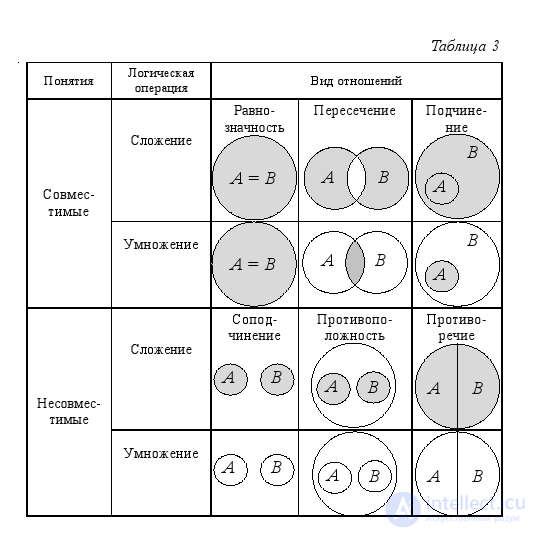
The results of the addition of concepts in the entire first line of the table. 3 (in equivalence, intersection and subordination) completely coincide with the results of addition in the entire third row of the table. 3 (in subordination, opposites and contradictions). And the results of multiplying the concepts in the entire second line of the table. 3 (in equivalence, intersection and subordination), on the contrary, do not completely coincide with the results of multiplication in the entire fourth row of the table. 3 (in subordination, opposites and contradictions).
Кроме того, результаты сложения понятий, при сравнении их с результатами умножения, полностью совпадают только в случае равнозначности, частично – в пересечении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трёх случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое.
Как правило, в естественном языке (том, на котором мы общаемся) результат сложения понятий выражается союзом «или», а умножения – союзом «и». В результате сложения понятий « школьник » и « спортсмен » образуется новое понятие, в объём которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объём нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.
О возможных разночтениях при употреблении союзов «или » и «и » говорит Виталий Иванович Свинцов в уже упоминавшемся нами учебнике по логике: «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределённое представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: « Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придётся признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но всё же использование союза «или» здесь следует признать предпочтительным» [3] .
1. Что такое логическая сумма и логическое произведение?
2. Возьмите три пары каких-нибудь понятий и проделайте с ними логические операции сложения и умножения, иллюстрируя их результаты с помощью круговых схем Эйлера.
3. Каковы результаты сложения и умножения понятий во всех случаях отношений между ними? Могут ли эти результаты полностью совпадать? Может ли логическая сумма или логическое произведение быть нулевым понятием?
4. Какой союз естественного языка является, как правило, выражением результата сложения понятий, какой – умножения? Проиллюстрируйте свой ответ самостоятельно подобранными примерами.
Comments
To leave a comment
Logics
Terms: Logics