Logics

This section provides a brief overview of all the fundamental concepts concerning logical representations and reasoning. The description of specific information about a particular form of logic is deferred to the next section. Instead, this section uses informal examples from the world of the vampus and from the familiar field of arithmetic. The authors adopted such a rather unusual approach, since the ideas of logic are much more versatile and attractive than is usually assumed.

Section 7.1 stated that knowledge bases consist of statements. These statements are expressed in accordance with the syntax of the representation language, which defines the form of all statements that are considered to be constructed correctly. The concept of syntax is fairly obvious in ordinary arithmetic: "x + y = 4" is a well-constructed sentence, but "x2y + =" is not. The syntax of logical languages ​​(and arithmetic as well) is usually formed in such a way that it is convenient to write articles and books with its help. There are literally dozens of different forms of syntax representation; in some of them, Greek letters and complex mathematical symbols are used, and in others, schemes with arrows and circles that are quite attractive in appearance. However, in all cases, statements in the agent knowledge base are real physical configurations (parts) of the agent. The formation of reasoning is reduced to the development of these configurations and manipulation of them.

Logic should also define the semantics of the language. Informal speaking, semantics relates to the “meaning” of statements. In logic, this definition becomes more accurate. The semantics of the language determines the truth of each statement as applied to each of the possible worlds. For example, the usual semantics adopted in arithmetic determines that the statement "x + y = 4" is true in a world where x is 2 and y is 2, but false in a world where x is equal to 1 and y is equal to 1. In standard logic each statement must be either true or false in each of the possible worlds - there cannot be any "intermediate states" in it.

In the future, if you need to clarify some definition, instead of the expression one of the “possible worlds” the term model will be used. (In addition, to indicate that the statement a is true in model t, the phrase "t is model a" will be used.) Possible worlds can be viewed as (potentially) real variations of the environment in which the agent may or may not be and models are mathematical abstractions, each of which establishes whether each statement relating to a given model is true or false. Informally, for example, you can consider x and y as the number of men and women who sit at the bridge table, and the statement x + y = A becomes true when the total number of players is four. In this case, formally admissible models are all possible assignments of integer values ​​to variables x and y. Each such assignment establishes the truth of any statement in arithmetic, the variables of which are x and y.

Now, after considering the concept of truth, we can move on to the topic of logical reasoning. To do this, it is necessary to define the concept of a logical consequence between statements - the idea that one statement can logically follow from another statement. The following notation is used in mathematical notation: a N p which means that the statement a entails the statement C. A formal definition of a logical consequence is as follows: a \ = C if and only if in any model in which the statement a is true, C is also true. Another way to express this thought is that if a is true, the statement C is also true. Informally speaking, the truth of the statement C "is contained" in the truth of the statement of a. The notion of a consequence is also used in arithmetic, for example, from the expression x + y = 4 follows the expression 4 = x + y. Obviously, in any model in which x + y = 4 (for example, in a model in which x is 2 and y is 2), it is also true that 4 = x + y. Soon it will be shown that any knowledge base can be considered as a statement, and in this book we will often talk about a statement from a certain knowledge base.

The analysis of the same type can be applied to the example of the reasoning about the world of vampus given in the previous section. Consider the situation shown in Fig. 7.2, b: the agent did not find anything in the square [1,1], and in the square [2,1] he felt a breeze. These perceptions, combined with the agent’s knowledge of the rules of the existence of the vampus world (described in PEAS, p. 286), constitute its knowledge base. The agent needs to know (among other things) whether there are pits in the adjacent squares, [1,2], [2,2] and [3,1]. In each of these three squares there may or may not be a hole, therefore (in this particular example) there are 23 = 8 possible models. They are shown3 in Fig. 7.4.

In models that contradict what the agent knows, the knowledge base becomes false; for example, the knowledge base is false in any model in which the square [1, 2] has a hole, since the breeze is not felt in the square [1, 1]. There are actually only three models in which the knowledge base is true, and they are shown in Fig. 7.4 as a subset of models. Now consider two possible conclusions:

OCi = "There is no pit in the square [1,2]"
0С2 = "There is no hole in the square [2,2]"

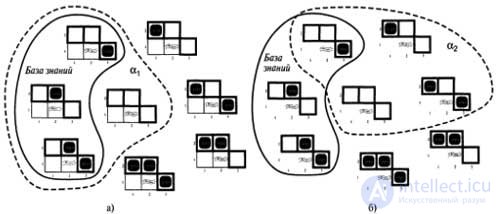Possible models describing the presence of pits in the squares [1,2], [2,2] and [3,1], which are based on the observations that there is nothing in the square [1,1], and in the square [2,1 ] there is a breeze: models with a knowledge base and saying ai (there is no hole in the square [1,2]) (a); models with a knowledge base and the statement a2 (squared [2.2] no pit) (b)

These models in Fig. 7.4, a and b are designated respectively as ar and a2. After analyzing all possible situations, we found the following: in each model in which the knowledge base is true, the statement ai is also true. Therefore, KB and OS]: there is no hole in the square [1,2]. In addition, one can be convinced of the following: in some models in which the knowledge base is true, the OSG statement is false. Why KB? a2: the agent cannot conclude that there is no hole in the square [2,2]. (In addition, he cannot draw a conclusion4 that there is a hole in the square [2.2].) In the previous example, not only the process of formation of logical consequences was illustrated, but it was also shown how the definition of logical consequence can be used to form conclusions, t. e. for carrying out logical inference. The logical inference algorithm illustrated in Fig. 7.4, is called model-based verification, since it examines all possible models to verify that statement a is true in all models in which the knowledge base is true. To better understand what a logical consequence and logical conclusion is, one can imagine that the set of all logical conclusions obtained from the database is a haystack, and the statement a is a needle. The logical consequence resembles the statement that there is a needle in the haystack, and the logical conclusion can be compared with its search. This distinction between the concepts of logical consequence and logical inference is also reflected in formal notation: if a certain algorithm of logical inference i allows one to infer a statement a from the KB knowledge base, then we can write the following: q hi a

This formula is read like this: "statement a is obtained by logical inference from the KB knowledge base using the algorithm i" or "algorithm i allows you to infer a statement a from the KB knowledge base". The algorithm of logical inference, which allows to get only such statements that really follow from the knowledge base, is called consistent, or preserving the truth. Consistency is a highly desirable feature. The controversial procedure of inference in the course of its work essentially creates what is not really: announces the detection of non-existent needles. It can easily be shown that the model validation algorithm, if applicable, is consistent.

The completeness property is also desirable: an inference algorithm is called complete if it allows one to deduce any statement that follows from the knowledge base. When it comes to real haystacks that have a finite volume, it seems quite obvious that systematic research always allows you to determine if there is a needle in a given haystack. But with many knowledge bases there is an infinitely large haystack, consisting of consequences, therefore ensuring fullness becomes an important issue6. Fortunately, there are complete inference procedures for many forms of logic that are expressive enough to cope with many knowledge bases.

Above, in fact, the process of formation of reasoning was described, the conclusions of which are guaranteed to be true in any world in which the premises are true; in particular, if the knowledge base is true in the real world, then any statement a obtained by a logical path from this knowledge base using a consistent inference procedure is also true in the real world.

So, despite the fact that the process of logical inference operates with "syntax" (and in fact with internal physical configurations, such as bits in registers or pictures of electrical excitations in brain structures), this process corresponds to the real world connections, according to which some aspects of the real world taking place7 due to the fact that there are other aspects of the real world. This correspondence between the world and its presentation is shown in Fig. 7.5.

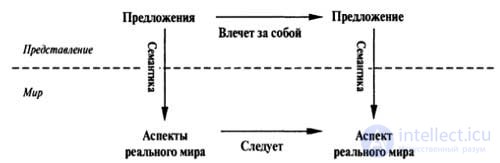Statements are the elements of the physical configuration of the agent, and the formation of reasoning is the process of creating new elements of the physical configuration from the existing ones. The process of forming logical reasoning must ensure that the new configuration elements represent those aspects of the world that really follow from the aspects represented by the existing configuration elements.

The last problem that needs to be solved in relation to logical agents is the problem of justification: establishing a connection between logical reasoning processes and the real environment in which an agent exists, if this relationship really exists. In particular, this problem concerns the question of how to know that the knowledge base is true in the real world? (After all, the knowledge base is just “syntactic constructions” in the agent’s head.) This is a philosophical problem, devoted a lot of books. The simple answer is that the specified connection is created using agent sensors. For example, our agent for the world of vampus has an odor sensor. Having found an unpleasant smell, the program of the agent creates the corresponding statement. This means that if this statement is indeed in the knowledge base, then it is true in the real world.

Therefore, the meaning and truth of the statements, in which the results of perceptions are expressed, are determined using the processes of forming sensations and making statements that they generate. And what can be said about the other knowledge of the agent, who, for example, believes that vampus can be found from neighboring squares, where does his unpleasant smell reach? This is not a direct representation of a single act of perception, but a general rule that may have been derived from the experience of perceptions, but not identical to the statements describing this experience. Learning is fraught with errors. It may turn out that vampuses spread an unpleasant smell on all days, except February 29 of a leap year, because these days vampuses are taking a bath. Therefore, in the real world, the knowledge base may not be true, but if the agent is equipped with good training procedures, he has reason for optimism.