Lecture
Judgment is an abstract thought in which something is affirmed or denied. The scheme of a simple judgment is as follows: S is (is not) P, where S is the subject of the judgment, i.e. the logical subject, what is being judged, P is the predicate of the judgment, i.e. logical predicate, what is awarded to the subject. Strictly speaking, a bundle of "to be" with or without negation is also included in the predicate, but to show that simple judgment is a relation of two concepts, one of which plays the role of a subject, and the other is a predicate, the link is presented as an independent element of the form .
Judgments are divided into types of quality and quantity . The quality of a simple judgment is its assertiveness or negativity. Its quantity is determined by the nature of the subject. If they judge something single, the judgment is called single, if any element of a set is common, if about a part of the elements of a set is private. Single and common judgments are often combined into one type, arguing something like this: the difference between the first and second is that the first, which is judged, consists of a single element. Leaving only two types by quantity (single plus common ones, on the one hand, and particular ones, on the other), they carry out a combined division of simple judgments in terms of quantity and quality and receive four types of categorical judgments.
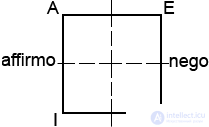
Logical square
It is convenient to get acquainted with the types of categorical judgments using the so-called "logical square": you need to draw a square, and in the vertices put the Latin letters A, E, I and O, which denote the types of judgments. To make it easier to remember these letters, the Latin word "affirmo" ("affirm") should be written to the left of the square, and "nego" ("I deny") should be written to the right. The arrangement of these words is not accidental. The fact is that on the left side of the square there are letters for two kinds of affirmative judgments, and on the right side for two kinds of negative ones. At the same time, in the upper part of the square, types of general plus single judgments are recorded, and in the lower part - private ones.
Since the first vowel in each of these Latin words gives a letter designation to a general (individual) judgment, and the second to a private one, it turns out that A is a general or a single statement, E is a common or a unit negative, I is a private statement, and O is a partial negation.
We now give examples of categorical judgments using the standard notation.
A: Every sperm whale is a whale (general statement). Mars is a planet (single statement).
E: No cat is a whale (total negation). Mars is not a star (single negation).
I: Some cats are (are) black.
A: Some cats are not (not) black.
Those who study logic often are perplexed about the standard form of expression of judgments, and sometimes come to sharp speeches against its use in any practical activity. They say that this form is completely artificial, that its use is violence against the Russian language, that if someone says so, it is only because the teachers of logic compel them to do so.
Despite the apparent immoderation of the charges, such claims should not be ignored, because they have a rational grain: to speak standardly always and everywhere is stupid. In everyday communication, we usually make judgments shorter and more elegant compared to what logic suggests, but very often the accuracy of the expression of thoughts becomes a victim of this brevity and elegance: phrases are vague, ambiguous, and sometimes ambiguous. If the case does not require maximum accuracy of communication, why not neglect it? But in some cases (for example, in scientific discussions, in court proceedings, etc.), it is necessary to express your thoughts very clearly, unequivocally. It is for such cases that the standard form of the expression of judgments has been developed.
The standard form of expressing judgments is necessary for the statement to be accurate.
|
|
Her feature, which immediately catches the eye, is the obligatory use of the verb-link "to be." The presence of this verb greatly simplifies the logical analysis of the judgment, because, firstly, it is easy to determine the quality of the latter (there is a negative particle before a bunch — negation, no — a statement), and secondly, it is easy to name concepts that play the role of subject and predicate (For example By moving from the non-standard form of the expression “Puppy is cold” to the standard “Puppy is experiencing cold,” it is much easier to correctly indicate the subject and predicate of this judgment: these are the concepts of “puppy” and “experiencing cold”, respectively.
|
The main features of the standard form of the expression of judgments are: 1) the presence of the verb-binding "to be" and 2) the use of standard quantifier expressions.
|
The second feature of the standard for categorical judgments is the strictly defined beginning of the corresponding statements (the exception is isolated judgments). Standardly begin with the following quantifier (determining the number of judgments, that is, quantitatively characterizing the subject) expressions: general statement - with the quantifier word "everyone" (options: "everyone", "any"), general negation - with the phrase "none" , private judgments - from the word "some".
In textbooks, a general statement, as a rule, is proposed to express, starting with the word “all,” but it is logically detrimental due to its ambiguity: in some cases, “all” means the abstract coverage of the elements of a given set (the elements are autonomous), in other cases - specific ( elements are connected to a whole). Example: "All my comrades are students" and "All my comrades are a friendly company."
As for private judgments, the following should be noted: formal logic uses the quantifier expression “some” in the sense of “at least one, and maybe everything”, but this meaning is rarely found in everyday communication. More often, "some" means "two or more, but not all."
How do categorical judgments of different kinds relate to each other? Before answering this question, we introduce a series of definitions.
1. The judgment of type A is compatible (incompatible) with the judgment of type B in truth (false), if there is (not) such a pair of specific judgments of these types about the same thing, that both of them are true (false). Here, in one phrase, four definitions are given: compatibility for truth, incompatibility for truth, compatibility for lies and incompatibility for lies.
2. From the judgment of type A follows the judgment of type B, if, in the true judgment of the first kind, the judgment of the second kind about the same is always true.
3. The relation of subordination: from the judgment of type A follows the judgment of type B, but from the judgment of type B does not follow the judgment of type A.
4. The relationship of contra-opposition (opposites): compatibility with falsehood and incompatibility with truth.
5. The ratio of subcontrability: the compatibility of truth and incompatibility of lies.
6. Contradiction relationship: incompatibility both in truth and in lie.
|
|
Now back to the categorical judgments. In the verticals of the "logical square" (between species A and I, on the one hand, and species E and O, on the other), there is a subordination relation; on diagonals (pairs A - O and I - E), the counter-dictor ratio, the upper side of the square (types A and E) - the ratio of contra-racy, lower (types I and O) - the ratio of subcontrariness.
|
Between categorical judgments of different types there are different types of relationships.
|
From simple judgments we move on to complex ones, i.e. to those in which there are at least two parts, which in turn constitute judgments. Difficult judgments are distinguished by logical connections between their parts. In this case, there are four main types:
1) Connective (conjunctive) judgments. Example: "It is raining and the sun is shining." There can be no union between parts either, but, if it can be put, the statement expresses a connecting judgment. Example: "It is raining, the sun is shining."
2) Dividing (disjunctive) judgments. There are two subspecies: a) non-strict dividing (Example: "Peter a checker player or a chess player") and b) strictly separating (Example: "Or Peter a checker player, or a chess player").
3) Conditional judgments. Here, too, there are two types: a) implicative (connection only by truth values) and b) causal (causal). Both types of conditional judgments are usually expressed using the "if ..., then" turn, but the meaning of this turn is different for each subspecies. Take for comparison two phrases: "If Moscow is the capital of Russia, then Paris is the capital of France" and "If Moscow is the capital of Russia, then it is the center of Russian political life." The first phrase expresses an implicative proposition (an abstract connection, according to truth values), the second one is causal (a connection of a concrete cause with a concrete consequence). Symbolic notation: for implicative judgment - A  B, for causal - A
B, for causal - A  AT.
AT.
4) Identifying judgments (judgments of equivalence). Standardly they are expressed with a turn "if and only if ... then". Example: "If and only if this month is February, then it is the shortest."
|
|
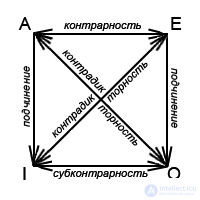
Relationship between judgments
on "logical square"
According to the availability of assessment information from the one who judges, judgments are divided into two types: assertive (in which there is no such assessment of information) and modal (there is such an assessment). It is always possible to get a modal from an assertoric judgment by entering a modal concept, i.e. the concept of some evaluation. For example, instead of an assertoric judgment “Earth is round,” you can get the modal judgments “It's good that the Earth is round,” “It is necessary that the Earth is round,” etc. By the nature of the assessment there are types of modalities.
Consider aletic modality. Aletic is a judgment with the modal notion of “necessary,” “possible,” or “accidental.” Aletic judgments with different modal concepts may be equivalent to each other. If the need to designate a rectangle, the possibility of a diamond, randomness a triangle, the letter "A" is an assertive judgment, and the symbol "~" is an equivalence of judgments, then equivalence schemes of alethic judgments will look like this:
one)  A ~
A ~ 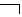
 A (Example: the judgment "In our time it is necessary to study logic" is equivalent to a judgment "In our time it is impossible not to study logic").
A (Example: the judgment "In our time it is necessary to study logic" is equivalent to a judgment "In our time it is impossible not to study logic").
2)  A ~
A ~ 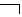
 A (Example: the judgment "You can make a mistake here" is equivalent to a judgment "It is not necessary that there be no error").
A (Example: the judgment "You can make a mistake here" is equivalent to a judgment "It is not necessary that there be no error").
3)  A ~
A ~  BUT
BUT 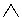

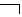 A (Example: the judgment "A gun shot accidentally" is equivalent to a judgment "A gun could shoot, but it could not shoot").
A (Example: the judgment "A gun shot accidentally" is equivalent to a judgment "A gun could shoot, but it could not shoot").
The denial of judgment is a logical operation, during which the truth value of a judgment is reversed . Usually they deny a lie, and they deny the truth only by a misunderstanding, therefore, citing the example of denial of judgment, one should proceed from a lie.
When denying a categorical judgment, the quantity and quality of the latter is reversed. Specification: for a single judgment the quantity does not change. Example: as a result of the rejection of the proposition "Every whale is a fish" the proposition is obtained "Some whales are not fish." For those who remember that in the formal logic “some” means “at least one, and maybe all”, there is no doubt about the truth of the judgment received. If, in this example, we declare the judgment “Neither a whale is not a fish” to be the result of a negation, then a logical error will occur: we will perform a negation incorrectly (not according to the rule of formal logic).
Schemes of denial of some complex judgments:
1) Denial of connective judgment. 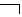 (BUT
(BUT 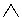 B) ~
B) ~ 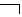 BUT
BUT 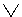
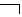 B. Example: as a result of rejecting the judgment “It is now overcast and rainy,” it turns out “Now it is not overcast or rainy.”
B. Example: as a result of rejecting the judgment “It is now overcast and rainy,” it turns out “Now it is not overcast or rainy.”
2) Denial of lax separation judgment. 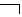 (BUT
(BUT 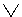 B) ~
B) ~ 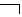 BUT
BUT 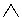
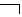 B. Example: Denying the judgment “Now the sun is shining or it is raining,” we get the judgment “Now the sun is not shining and it is not raining.”
B. Example: Denying the judgment “Now the sun is shining or it is raining,” we get the judgment “Now the sun is not shining and it is not raining.”
3) Denial of causal judgment. 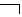 (BUT
(BUT 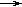 B) ~
B) ~  (BUT
(BUT 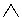
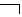 AT). Example: rejecting the statement "If a student is an excellent student, he loves logic," we get the statement: "A student may be an excellent student, but not like logic."
AT). Example: rejecting the statement "If a student is an excellent student, he loves logic," we get the statement: "A student may be an excellent student, but not like logic."
|
|
Comments
To leave a comment
Logics
Terms: Logics