Lecture
The most developed of the basic forms of abstract thinking is inference — an abstract thought, in which the conclusion (new judgment) is derived from the premise (initial judgment). The conclusion is the logical transition from the premise to the conclusion.
Inference is used to expand knowledge: rules of inference are formulated so that the original truth leads to a new one. It should be remembered that if the premise contains some kind of falsehood, no rules of logic can guarantee the truth of the conclusion. In this case, the conclusion loses practical meaning, for successful practice is possible only on the basis of true knowledge of the world.
According to the definition given above, any inference can be written in the form of a simple scheme:
P
---.
H
Here, P is the premise, G is the conclusion, and the bar denotes a conclusion (read: "therefore").
Where does a huge variety of conclusions come from, if they all obey a simple three-term scheme? The fact is that, firstly, the premise and the conclusion can be not a simple, but a complex judgment, sometimes a multilink complex of judgments, and secondly, the conclusion can be carried out according to different rules.
|
There are two types of output: credible and plausible (the first one guarantees the truth of the conclusion with true assumptions, the second one does not). Hence the division of conclusions into reliable and plausible. Previously, it was decided to allocate not two, but three types of inference: deduction (transition from general knowledge about the subject to the particular), induction (transition from private knowledge to the general) and analogy (transfer of knowledge about one subject to another). Accordingly, there were three types of conclusions: deductive, inductive, and by analogy. How does this traditional three-term division of reasoning relate to the two-member given above? All deductive conclusions are reliable, and it is clear why: if true general knowledge (knowledge of all the elements of a given set) is true, then private knowledge is true (knowledge of a part of the elements of the set). But conclusions with induction and analogy, as a rule, are plausible, since, firstly, true knowledge of some elements of the set may turn out to be false for other elements, and, secondly, an object to which, by analogy, the properties of another object are attributed, may not have these properties. The exception to the rule: the inference with full generalizing induction (which will be discussed below) is reliable. We will pay the main attention to deductive conclusions, because, because of their authenticity, they traditionally enjoy the greatest respect from representatives of formal logic. In this case, the simplest deductive schemes will be considered. |
|
First of all, let us turn to immediate conclusions, i.e. to those in which the conclusion is a transformation of a single premise, which is a categorical judgment. There are three main types: “logical square” derivation, inversion and transformation. The conclusion on the "logical square" is used for general judgment - affirmative or negative. In this case, they move from top to bottom along the vertical of the "logical square", i.e. go to the appropriate premise of private judgment. Example: Every carp is a fish. Now about the rules of treatment. The basic rule is very simple: when converting, the subject and the predicate of the parcel are swapped. But besides this rule, there are two limitations to keep in mind: first, the general statement is replaced by a private one, and second, for particular negative judgment, no appeal is made. Example: Every carp is a fish. The rule of transformation: the quality of the parcel is reversed, and its predicate is taken with denial. Example: Every carp is a fish.
|
1. Conditionally categorical conclusions.
Modus ponens (asserting conditionally categorical inference):
BUT 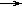 B, A
B, A
____________
AT
Example: "If this gas is neon, then it is inert. This gas is neon. Therefore, it is inert."
Modus tollens (denying conditional categorical conclusion):
BUT 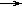 AT,
AT,  AT
AT
___________
 BUT
BUT
Example: "If this gas is neon, then it is inert. This gas is not inert. Therefore, it is not neon."
|
2. Separating-categorical conclusions. Modus ponendo-tollens (affirmative-deny separation-categorical reasoning). This scheme has two options:
Example (for the first option): "Either I am at home or I am away from home. I am at home. Therefore, it is not true that I am away from home." Modus tollendo-ponens (denial-affirming separation-categorical inference). This scheme also has two options:
Record "
|
3. Dilemmas.
Dilemmas come in four forms:
|
Dilemma |
constructive |
destructive |
|
simple |
A |
A |
|
complex |
A |
A |
An example of a complex structural dilemma: "If it is raining outside, it is wet, if it is icy, it is slippery. It is raining or icy outside. Therefore, it is wet or slippery."
4. Conditional inference.
1) Contraposition:
BUT 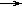 AT
AT
_______
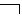 AT
AT 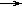
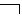 A
A
Example: "If it rains, it is wet outside. Therefore, if it is not wet outside, it does not rain."
2) Difficult contraposition:
BUT 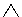 B
B 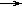 C
C
________
A 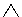
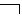 C
C 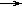
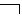 B
B
Example: "If the iron is serviceable and is included in a working network, it heats up. Therefore, if the iron is serviceable and does not heat up, then it is not included in the working network."
3) Transitivity:
BUT 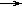 B, B
B, B 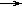 C
C
_________
BUT 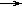 C
C
Example: "If this number is three, then it is more than two. If this number is more than two, then it is more than one. Therefore, if this number is three, then it is more than one."
4) Export:
BUT 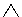 B
B 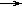 C
C
_____
A 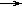 (B
(B  C)
C)
Example: "If the matter is familiar and interesting, then it goes well. Therefore, if the matter is familiar, then if it is interesting, it goes well."
5) Import:
A  (B
(B  C)
C)
______
BUT  B
B  C
C
To give an example of importing, you can take the previous example by reversing the package and conclusion.
The last class of deductive reasoning that you should be aware of in this logic course is simple categorical syllogism, i.e. a conclusion consisting of three categorical judgments: two premises and a conclusion. This conclusion includes three concepts, each of which is used twice. They are called the terms of the syllogism (the two extreme - the smaller and the larger - and the middle terms) and denoted by the Latin letters S, P and M.
Where did such designations come from and how to find the terms of the syllogism? Consider a classic example that has been walking through the textbooks of logic since pre-revolutionary times: "All people are mortal. Socrates is a man. Therefore, Socrates is mortal." Writing down all the judgments and the whole syllogism is strictly standard, we get the following form:
Every man is mortal.
Socrates is a man.
___________________
Socrates is mortal.
The logical analysis of a specific syllogism is best to start with a conclusion. The fact is that in concluding a correctly composed simple categorical syllogism, a smaller term always plays the role of a subject, and a larger one - a predicate. Hence the letters for the extreme terms - S and P. In this example, S is Socrates, P is mortal (being). Well, as the term M (from the Latin word "medius" - "medium"), the notion of man appears here.
The location of the terms distinguish the figures of a simple categorical syllogism. A total of four, denoted by Roman numerals:
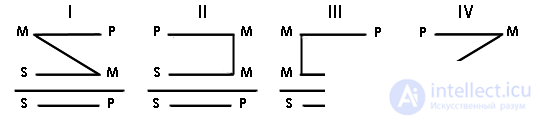
|
Each figure has modes - forms, determined by the types of categorical judgments of which syllogism consists. Moreover, the types of judgments need to be determined strictly sequentially, moving from top to bottom according to the figure's diagram. For example, the EIO modus takes place when the larger (top on the diagram) premise is of type E, the lesser is of type I, and the conclusion is of type O. As for the Socrates conclusion, this is the AAA I figure of the figure. For each figure, a set of correct modes was revealed, i.e. those that guarantee the truth of the conclusion under the true assumptions. Here are these modes:
Knowledge of the correct modes helps to quickly determine the truth of the syllogism. For example, having found out that the conclusion about Socrates has true premises and that it belongs to the AAA I mode of a simple categorical syllogism figure, i.e. to one of the correct modes of this figure, there is no doubt that this reasoning is true. Now a few words about the conclusions with induction and analogy. As for the first, here the main type is incomplete generalized induction. If {K} is the set of interest to us, {S} is a subset of this set, Si is an element of the {S} subset, P is an attribute of interest to us, then the scheme of this type of inductive inferences will look like this: S1 - P Example: I wanted to find out if a lot of textbooks ({K}) have the feature "to have a hard cover" (P). A lot of textbooks are very large, so I limited myself to researching the subset of the “textbook of my home library” ({S}). All the books of this subset were in hardcover. I make an inductive conclusion: "Perhaps every textbook has a hard cover." The word "possibly" means that the conclusion does not exclude an error. And it is clearly present in the inductive research I carried out: why should not the textbook be in paperback? If I was only interested in a lot of textbooks in my home library, then my conclusion would be reliable. This would be a total generalized induction: S1 - P
|
Inference by analogy is such a conclusion in which, on the basis of the similarity of two objects in some properties, they conclude that they are similar in other properties . Let similar objects be R1 and R2, and properties of objects be a, b, c, and d. Then the inference scheme by analogy can be written as:
R1 - a, b, c, d
R2 - a, b, c
---------
Perhaps R2 - d.
A classic example is the emergence of a hypothesis about the existence of life on Mars. Observing Mars through telescopes, astronomers have found a great resemblance to Earth. Since there is life on Earth, it was assumed that it is on Mars. This hypothesis has not yet been confirmed.
Why, despite the possibility of errors, induction and analogy are widely used in practice? The fact is that in serious studies such conclusions are used not in pure form, but in combination with deduction.
Comments
To leave a comment
Logics
Terms: Logics