Determination of Feasibility

Now let's consider what performance indicators DPLL and WalkSAT algorithms demonstrate in practice. We are particularly interested in difficult problems, because the lungs can be solved with the help of any old algorithm. In the previous section, we familiarized ourselves with some surprising discoveries in the field of solving problems of a certain type.

For example, a problem with n queens (which was once considered to be extremely difficult) when solved with the help of search algorithms with returns turned out to be trivially simple for local search methods, such as the method with minimal conflicts. This is due to the fact that the solutions to this problem are distributed in an assignment space very densely and for any initial assignment it is guaranteed that the solution is close. Thus, the problem with n queens is simple because it is not sufficiently limited .

If we are talking about solving feasibility check problems presented in conjunctive normal form, then among them, problems that contain relatively few expressions that restrict the values ​​of variables can be considered insufficiently limited. For example, the following is a randomly crafted 3-CNF statement with five characters and five expressions.

(¬D v ¬B v C) ^ (B v ¬A v ¬ C) ^ (¬ C v ¬ B v E) ^ (E v ¬ D v B) ^ (B v E v ¬ C)

The models of this statement are 16 out of 32 possible assignment options, so on average, only two randomly selected hypotheses will be required to search for a model.

So where do you find challenging tasks? It can be assumed that if the number of expressions is increased, while the number of characters remains constant, the task will become more limited and the search for solutions will be more difficult.

The figure shows the probability that a randomly formed statement in the form of a 3-CNF is feasible, as a function of the expression / symbol ratio, m / n, with a constant value of n equal to 50. As expected, with small values ​​of m / n this probability is close to 1, and for large values ​​of m / n the probability is close to 0. On the probability curve, a rather sharp decline begins approximately after reaching the value m / n = 4.3. Statements in the form of CNF, approaching this critical point, can be called "almost doable, or" almost impossible. Can we assume that it is here that there are difficult tasks?

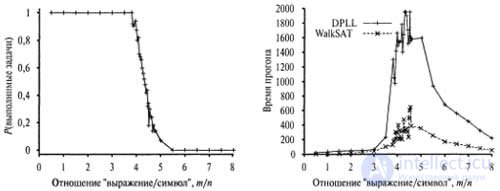
Performance analysis of DPLL and WalkSAT algorithms in solving difficult problems: a graph that shows the probability that a randomly formed statement in the 3-CNF form with the number of symbols n = 50 will be feasible as a function of the expression / symbol ratio, m / n (but); graph of the average runtime of the DPLL and WalkSAT algorithms for 100 executable randomly generated statements in the form of 3-CNFc n = 50, which shows the presence of a narrow range of m / n values ​​around the critical point (b)

The figure shows the runtime of the DPLL and WalkSAT algorithms in the area around this critical point, where our attention was limited to only executable tasks. The study of these results allows us to draw three conclusions: first, tasks approaching the critical point are much more difficult compared to other randomly formed tasks; secondly, even when solving the most complex tasks, the DPLL algorithm is very efficient - it requires an average of several thousand steps to be completed compared to the value of the number of steps 2 ⁵⁰ = 10 ¹⁵ , which is required for iterating over the truth table; thirdly, the WalkSAT algorithm works much faster than the DPLL algorithm in all this range of task characteristics.

Of course, these results relate only to randomly formed tasks. Real tasks do not necessarily have the same structure as randomly formed tasks (they can be characterized by different values ​​of the relative number of positive and negative literals, different connection densities between expressions, etc.). However, in practice, the WalkSAT algorithm and similar algorithms also do very well with solving real-world problems and are often not inferior to the best special-purpose algorithms for these tasks.

Problem solvers such as Chaff easily cope with tasks consisting of thousands of characters and millions of expressions. Based on these observations, it can be concluded that some combinations of heuristics with minimal conflicts and random walk behaviors provide a universal ability to find solutions in most situations in which combinatorial reasoning is required.