Lecture
The language of predicate logic is one of the artificial languages of modern formal logic. Before we begin to consider it, we will clarify which languages are called natural and artificial and how they relate to each other.
Natural languages are the languages of natural groups: Russian, German, Chinese, etc. All other languages are artificial.
Natural and artificial languages are opposed to each other. To verify this, we note the main differences between them.
First, they differ in the nature of occurrence. Natural language arises spontaneously, no one deliberately creates it. People need to communicate with each other, and without language it is impossible. Here and there is a language, and it arises naturally, without prior deliberation. On the contrary, at first someone comes up with an artificial language, and only then he starts to fulfill his role as an intermediary in communication.
The second distinction follows from the peculiarities of occurrence: a natural language has no specific authors, and an artificial one has at least one such author. Take for example the Russian language. Can we say that who created it? You can: it was created by the people. But at the same time, no representative of the Russian people can claim to be authorship in relation to their language. This language was created not by any specific authors, but by the whole nation. Another thing - artificial languages. We may not know their specific authors, as, for example, it is the case with the ancient ciphers, but the fact that every artificial language has at least one such creator is not in doubt. Sometimes about the author says the name of an artificial language. A striking example is the language commonly known as Morse code.
Third, natural and artificial languages are distinguished by their scope: in the first, it is universal, and in the second, local. The universality of the use of natural language means that it is used in all activities without exception. But artificial language is not used everywhere. This means the local nature of the application. Let's go back to the Morse language. Where is it used? As a rule, where it is necessary to transmit information using electromagnetic waves.
Fourthly, natural and artificial languages are qualitatively different systems. The first one is an open system, i.e. The system is incomplete and in principle not complete. As human activity develops, their native language should develop as well. The open character of any natural language as a system is indicated by the presence of such expressions in it, which are exceptions to the rules, but are used along with the correct expressions.
Another thing - an artificial language. Ideally, this is a closed (completed, completed) system in which everything goes strictly by the rules, in which there are no exceptions to the rules. The presence of at least one incorrect expression is considered a major drawback of an artificial language, and try to eliminate this drawback as quickly as possible.
The main differences between natural and artificial languages can be presented as a table:
| Base of comparison | Natural language | Artificial language |
| 1. Appearance | Spontaneous | Specially organized |
| 2. The presence of a specific author | Not | there is |
| 3. Scope of application | Universal | Local |
| 4. The specifics of the system | Openness | Closeness |
So, natural and artificial languages are so different in relation to each other that they should be considered as opposite sign systems. However, despite the opposite, they converge, which is especially clearly seen in our time.
On the one hand, school textbooks of natural languages are created by the efforts of linguists. Studying the native language at school is a must for a modern person. This makes natural language communication more rigorous, and rigor is one of the main properties of artificial languages. Compare Russia at the beginning of the 20th and 21st centuries. At the beginning of the twentieth century, the overwhelming majority of the population of our country spoke dialects of the Russian language, which is not surprising under the conditions of mass illiteracy. Numerous dialects made it difficult for people from different regions to communicate. In our time, the situation is quite different: the majority of Russians speak the same language.
On the other hand, artificial languages are becoming increasingly flexible, and due to this, they interfere in all kinds of activities, i.e. acquire the universal nature of the application, characteristic of natural languages. This is easily illustrated by the example of computer languages. Nowadays, none of the main areas of modern society can do without computers, and working on a computer requires knowing, if not programming languages, then at least the languages of specific programs.
The convergence of natural and artificial languages will inevitably lead to their merging, but this will not happen soon. It is not necessary to artificially speed up the rapprochement, which is indicated, in particular, by the history of the language Esperanto. It appeared at the end of the 19th century as a means of communication for Indo-European peoples. At the same time, the creator of Esperanto pursued a good goal: so that no one was hurt, let different nations speak an artificial language common to them. By and large, the idea failed. Yes, Esperanto has not disappeared at all: it is used in some places in modern international communication, but it is not widely spread.
Now back to the logic. Currently, there are many artificial formal-logical languages. There are hundreds of them, but they are all built according to similar principles, so familiarity with one of them makes it easy to master others if necessary.
Consider the language of predicate logic. In his alphabet, the following characters:
1) p, q, r, s, p 1 , ... are propositional variables (symbols for sentences);
2) a, b, c, d, a 1 , ... are individual constants (symbols for single names);
3) x, y, z, x 1 , ... are individual variables (symbols for common names);
4) P, Q, R, S, P 1 , ... - predictors (symbols for features, as well as properties and relations);
five) 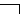 (the sign of denial is read: "not" or "wrong, that"),
(the sign of denial is read: "not" or "wrong, that"), 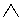 (a conjunction sign, i.e. a compound, is read: "and"),
(a conjunction sign, i.e. a compound, is read: "and"), 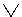 (the sign of a non-strict, or simple, disjunction, i.e. a non-strict, or simple, separation, is read: "or"),
(the sign of a non-strict, or simple, disjunction, i.e. a non-strict, or simple, separation, is read: "or"), 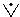 (the sign of a strict disjunction reads: "or ..., or"),
(the sign of a strict disjunction reads: "or ..., or"), 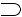 (the implication sign reads "if ... then"),
(the implication sign reads "if ... then"), 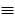 (the equivalence sign reads: "if and only if ..., then"),
(the equivalence sign reads: "if and only if ..., then"), 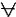 (quantifier of universality, read: "all", "everyone", "any"),
(quantifier of universality, read: "all", "everyone", "any"), 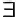 (the quantifier of existence is read: "there is such ... that" or "some") are logical symbols;
(the quantifier of existence is read: "there is such ... that" or "some") are logical symbols;
6) (,) (brackets),, (comma) - service characters.
Thus, the alphabet contains symbols for the main semantic categories. The strict meaning of the negation sign and the signs of logical connectives (conjunction, disjunction, implication, and equivalence) are specified using truth tables. If A and B are utterances, 0 is false, and 1 is true, in two-digit logic, i.e. in such logic, where the statement can be either false or true, and the third is not given, these tables have the following form:
|
|
Note that the logical symbols presented in the tables are distinguished by their binding strength, in descending order of which they are arranged as follows: 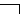 ,
, 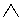 ,
, 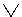 ,
, 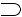 ,
,  . Taking into account the strength of the binding reduces the number of brackets in logical formulas. Suppose we need to investigate the formula (p
. Taking into account the strength of the binding reduces the number of brackets in logical formulas. Suppose we need to investigate the formula (p 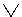 q)
q) 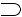 r ("if p or q, then r"). Since the disjunction is stronger than implication, we can remove the parentheses: p
r ("if p or q, then r"). Since the disjunction is stronger than implication, we can remove the parentheses: p 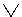 q
q 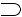 r. The resulting formula is read in the same way as the original one. Sometimes brackets should not be removed. For example, in the formula (p
r. The resulting formula is read in the same way as the original one. Sometimes brackets should not be removed. For example, in the formula (p 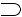 q)
q) 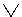 r ("if p, then q, or r") p and q are more connected than q and r, and if you remove the brackets, the ratio will be reversed.
r ("if p, then q, or r") p and q are more connected than q and r, and if you remove the brackets, the ratio will be reversed.
Logical formulas are sentences of an artificial symbolic (mathematical) language, i.e. modern formal, logic. They can include only the characters of the alphabet, and write these formulas, as well as the formulas of mathematics, follow the rules of syntax.
The definition of a correctly constructed formula (PFR) of the predicate logic language is given in four steps:
1) the propositional variable is PPF;
2) an expression of the form A (t 1 , t 2 , ..., t n ), where A is a predictor and t k is an arbitrary individual symbol from the sequence given in brackets, is a FFT;
3) if B and C - PPF, and 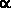 - individual variable, then expression of the form
- individual variable, then expression of the form 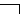 B, B
B, B 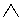 C, B
C, B 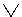 C, B
C, B 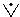 C, B
C, B 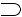 C, B
C, B  WITH,
WITH, 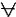
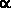 AT,
AT, 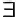
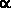 B - PPF;
B - PPF;
4) nothing else is PPF.
It can be seen that the definition is given very strictly, and this is not accidental: we noted above that severity is a distinctive feature of artificial languages.
Now we give examples of formulas of the language of predicate logic. Take the proverb "The language will bring to Kiev." The easiest way to write a formula for this statement is to use a propositional variable. It will be very simple: p. But according to the second paragraph of the definition of the PPF, we can construct a longer sentence in the language of the predicate logic: 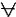 xP (x), where x is the language, P - to be able to bring to Kiev. This sentence reads like this: "For any x P from x". If we take into account that the sign "to be able to bring to Kiev" contains a two-place attitude, then the formula will come out even longer:
xP (x), where x is the language, P - to be able to bring to Kiev. This sentence reads like this: "For any x P from x". If we take into account that the sign "to be able to bring to Kiev" contains a two-place attitude, then the formula will come out even longer: 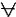 xP (x, a), where x is the language, and Kiev, P to be able to bring to (something).
xP (x, a), where x is the language, and Kiev, P to be able to bring to (something).
What does any logical formula express? It expresses the logical form of this statement, i.e. the form of abstract thought that is contained in it. This form appears in artificial languages of logic in a form convenient for logical analysis: briefly and precisely.
Let us consider with an example how, analyzing with the help of truth tables, a logical formula of a complex utterance, they reveal the conditions of its truth, or, in other words, how a tabular study of the logical form of a truth statement is conducted.
In the formula p 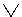 q
q 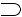 r three different propositional symbols, each of which can have one of two truth values — either true or false. We calculate, using the combinatorics rule, the number of combinations of these values for three characters: 2 3 = 8. This means that there will be eight rows in our table. With two propositional characters, there would be only four lines (2 2 = 4).
r three different propositional symbols, each of which can have one of two truth values — either true or false. We calculate, using the combinatorics rule, the number of combinations of these values for three characters: 2 3 = 8. This means that there will be eight rows in our table. With two propositional characters, there would be only four lines (2 2 = 4).
Now let's start building the table, writing down the values of the characters in the column under each of them:
| R | 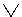 |
q | 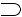 |
r |
| 0 0 0 0 one one one one |
0 0 one one 0 0 one one |
0 one 0 one 0 one 0 one |
Attention should be paid to the combination search algorithm: under the first character we write four times "0" and four times "1", under the second - in pairs "0" and "1", under the third - alternately "0" and "1". As a result, none of the lines repeats the others and all combinations of truth values are taken into account. It remains to conduct a study of the logical constants contained in the formula, in accordance with their semantic values:
| R | 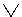 |
q |  |
r |
| 0 0 0 0 one one one one |
0 0 one one one one one one |
0 0 one one 0 0 one one |
one one 0 one 0 one 0 one |
0 one 0 one 0 one 0 one |
The truth of this formula is determined by the penultimate column. We see that not all combinations of the truth values of propositional symbols result in true. In the study of forms of statements, there are three options. First, the formula, as in our case, may be feasible, i.e. there are combinations of the meanings of propositional characters that lead to truth, but there are also those that do not. Secondly, the formula may turn out to be identically true (universally significant, or the law of symbolic logic). In this case, for any set of variable values, the result is true. Third, the formula may turn out to be identically false, i.e. for any set of variable values that are false. 
Comments
To leave a comment
Logics
Terms: Logics