Forward and reverse output

Due to this completeness, the resolution algorithm becomes a very important inference method. However, in many practical situations, the full power of the resolution rule is not required. Real knowledge bases often contain only expressions in a limited form, called ^ horn expressions. The Horn expression is a disjunction of literals, among which no more than one is positive. For example, the expression (¬L _1,1 v ¬Breezev B _1,1 ), where L _1,1 means that the location of the agent is a square [1,1], is a Horn expression, whereas the expression (¬B _1.1 v P _1,2 v P _2,1 ) is not.

The restriction that only one literal of an expression should be positive may seem a bit far-fetched and unpromising at first glance, but in fact is very important for the three reasons described below.

Each Horn expression can be written as an implication, the background of which is a conjunction of positive literals, and the conclusion is one positive literal. For example, the Horn expression (¬B _1,1 v P _1,2 v P _2,1 ) can be written as an implication (L _1,1 ^ Breeze) => B _1,1 . In this last form, this statement becomes easier to read: it states that if the agent is in the square [1,1] and feels the breeze, then the breeze is felt in the square [1,1]. It is easier for people to read and write statements in such a form, concerning many areas of knowledge. Horn expressions like this, having exactly one positive literal, are called definite expressions . Such a positive literal is called an expression head , and negative literals form an expression body . A definite expression without negative literals simply states the validity of a certain statement; such a construction is sometimes called a fact . Certain expressions form the basis for logical programming . The Horn expression without positive literals can be written as an implication whose conclusion is the False literal. For example, the expression (¬W1,1 v ¬W1,2), according to which a vampus cannot be simultaneously in squares [1,1] and [1, 2], is equivalent to the expression W _1,1 ^ W _1,2 => False . In the database world, such statements are called integrity constraints and are used to detect errors in data. The following algorithms, for simplicity, assume that the knowledge base contains only certain expressions and does not contain integrity constraints. Such knowledge bases we will call being in the horns form.

Inference using Horn expressions can be carried out using forward logic inference and inverse inference , which are discussed below. Both of these algorithms are very natural in the sense that the stages of logical inference are obvious to people and can be easily followed.

Obtaining logical consequences using Horn expressions can be carried out in a time linearly dependent on the size of the knowledge base.

This last fact becomes a particularly pleasant surprise. It means that the procedure of inference is very inexpensive in relation to many propositional knowledge bases that are encountered in practice.

Algorithm direct logic output PL-FC-Entails? (KB, q) determines whether a single propositional character q (query) follows from the knowledge base, presented in the form of Horn expressions. He begins work with known facts (positive literals) in the knowledge base. If all the prerequisites of a certain implication are known, its conclusion is added to the set of known facts. For example, if it is known that the facts L _1,1 and Breeze take place, and the knowledge base contains the expression (L _1,1 a Breeze) => B _1,1 , then fact B _1,1 can be added to it. This process continues until a query q is added to the knowledge base or it becomes impossible to make further logical inference. This detailed algorithm is shown in the listing; the main thing that should be remembered about him is that he acts in time determined by linear dependence.

Direct Inference Algorithm for Propositional Logic. The list of the agenda traces characters for which it is known that they are true, but which are not yet "processed." The count table tracks information about how many prerequisites for each implication are not yet known. Each time a new character p is processed from the list of “agenda” characters, the number of prerequisites in the count table is shortened by one for each implication in which the premise p appears. (Such implications can be detected in constant time if the KB knowledge base has been indexed properly.) After the number of unknown prerequisites for a certain implication reaches zero, all these prerequisites become known, therefore the conclusion of this implication can be added to the agenda list. Finally, you need to keep track of which characters have already been processed; a symbol deduced from a logical path should not be added to the page regenda if it has already been processed. This avoids unnecessary work, and also prevents the occurrence of infinite loops that can be caused by the presence of such implications as P => Q and Q => P

function PL-FC-Entails? (KB, q) returns true or false

   inputs : KB, knowledge base - many propositions

horn expressions

q, query is a propositional symbol

   local   variables : count, table indexed by statements,

originally sized,

prerequisite

inferred, character-indexed table

in which each entry is originally

is false

agenda, list of characters, initially includes

characters known as true

KB knowledge base

   while agenda list is not empty do

p <r- Pop {agenda)

unless inferred [p] do

inferred [p] <- true

   for   each is a horn expression with which is present

background p do

decrease by one the count value [s]

if count [s] = 0 then do

if Head [s] = q then return true

Push (Head [c], agenda)

return false

The best way to understand this algorithm is to look at an example and an illustration. The figure, a, shows a simple knowledge base from Horn expressions, containing Ive's expressions as known facts. The figure shows the same knowledge base, depicted as ^ graph AND-OR. In the AND-OR columns, multiple arcs connected by a curved line denote a conjunction (they need to prove the truth of each arc), and multiple arcs not connected to each other denote a disjunction (it is enough to prove the truth of any of these arcs). On this graph, you can easily check how the direct inference algorithm operates. The values ​​of the known leaf nodes are set (in this case, L and b), and the process of logical inference spreads up the graph as long as it is possible. With the appearance of any conjunction, the process of propagation stops and waits until all conjuncts become known, and only after that does it continue. We recommend the reader to work out this example in detail.

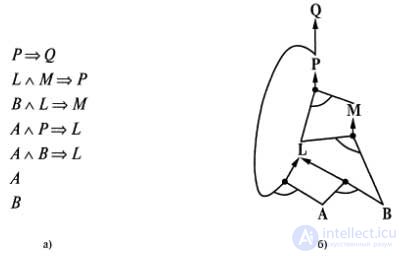
An example of the application of the direct inference algorithm: a simple knowledge base consisting of Horn expressions (a); the corresponding graph AND-OR (b)

It is easy to make sure that the direct inference algorithm is consistent : each step of the inference is essentially an application of the separation rule. In addition, the algorithm of direct inference is complete: it can be obtained every atomic statement, which follows from the knowledge base. The easiest way to verify this is to consider the final state of the inferred table (after this algorithm reaches a fixed point at which any new stages of logical inference become impossible).

This table contains the value true for each character derived by the logical path during this process, and false for all other characters. This table can be considered as a logical model; moreover, ^ every definite expression in the original KB knowledge base is true in this model. To verify this, we assume the opposite, namely that some expression a1 l ... l ak => b from the knowledge base is false in this model. Then in this model the expression a1 l ... l ak must be true and in it the expression b must be false. But this contradicts our assumption that the algorithm has reached a fixed point! Therefore, we can conclude that the set of atomic statements, obtained by a logical way by the time of reaching a fixed point, determines the model of the initial knowledge base square. Moreover, any atomic statement d, which follows from the KB knowledge base, must be true in all its models, as well as, in particular, in this model. So, any statement d, which follows from the knowledge base, should be derived from a logical data algorithm.

Direct inference is an example of the application of the general concept of the formation of logical reasoning, ^ data-driven, i.e. reasoning in which the focus of attention is initially focused on known data. Direct inference can be used in any agent to obtain conclusions based on incoming perceptual results, often without even taking into account any specific request. For example, an agent for the vampus world can communicate with the Tell operation the results of its perceptions of the knowledge base using the incremental direct inference algorithm, in which new facts can be added to the "agenda" to initiate new inference processes. In humans, the formation of data-driven reasoning, to a certain extent, occurs as new information becomes available. For example, being at home and hearing that it started to rain, a person who was going to have a picnic might decide that he would have to cancel it. But such a decision is unlikely to be made if he finds out that the seventeenth petal of the largest rose in his neighbor’s garden turned out to be wet; people keep direct inference processes under careful control, since otherwise they would simply be flooded with a stream of logical conclusions that have nothing to do with reality.

The reverse logic inference algorithm, as its name indicates, acts in the opposite direction from the request. If you can immediately find out that the statement contained in the query q is true, then you do not need to do any work. Otherwise, the algorithm finds those implications in the knowledge base, from which g follows. If one can prove that all the premises of one of these implications are true (using a reverse inference), then the statement g is also true. Being applied to the query Q shown in the figure, this algorithm will go down the graph until it reaches the set of known facts that form the basis for the proof. The development of a detailed algorithm is left to the reader as an exercise; as in the case of the direct inference algorithm, the effective implementation of this algorithm performs its work in linear time.