Lecture
Простые суждения делятся на сравнимые и несравнимые.
Comparable (identical in material) judgments have the same subjects and predicates, but may differ by quantifiers and bundles. For example, the judgments: “ All schoolchildren study mathematics ”, “ Some schoolchildren do not study mathematics ” - are comparable: they have the same subjects and predicates, and quantifiers and bundles are different. Incomparable judgments have different subjects and predicates. For example, judgments: “ All schoolchildren study mathematics ,” “ Some athletes are Olympic champions ,” are incomparable: the subjects and predicates they do not match.
Comparable judgments are, like concepts, compatible and incompatible and can be in different relationships with each other.
Compatible statements are judgments that can be true at the same time. For example, judgments: “ Some people are athletes ,” “ Some people are not athletes ,” are both true and constitute compatible judgments.
Judgments that cannot be true at the same time are called incompatible : the truth of one of them necessarily means the falsity of the other. For example, judgments: “ All schoolchildren study mathematics,” “Some schoolchildren do not study mathematics ,” cannot be true at the same time and are incompatible (the truth of the first judgment inevitably leads to the falsehood of the second).
Compatible judgments may be in the following relationships:
1. Equivalence is a relationship between two judgments, in which both the subjects, the predicates, the connectives, and the quantifiers coincide. For example, judgments: “ Moscow is an ancient city ”,
" The capital of Russia is an ancient city ", - are in relation to equivalence.
2. Subordination is a relationship between two propositions, in which the predicates and bundles coincide, and the subjects are in relation to species and genus. For example, the propositions: “ All plants are living organisms ,” “ All flowers (some plants) are living organisms ,” are in respect of submission.
3. Partial coincidence (subcontractivity) is a relationship between two judgments, in which the subjects and predicates are the same, and the bundles are different. For example, the propositions: “ Some mushrooms are edible ,” “ Some mushrooms are not edible ,” are in terms of partial overlap. It should be noted that in this regard there are only private judgments - privately affirmative ( I ) and privately negative ( O ).
Incompatible judgments may be in the following relationships.
1. The opposite ( contra ) is a relationship between two judgments, in which the subjects and predicates are the same, and the bundles are different. For example, the propositions: “ All people are truthful ,” “ All people are not true ,” are in opposition. In this regard, there can only be general judgments - general affirmative ( A ) and generally negative ( E ). An important sign of opposing judgments is that they cannot be true at the same time, but they can also be false. Thus, the two opposing judgments cannot be true at the same time, but they can be false at the same time: it is not true that all people are true, but it is also not true that all people are not true.
Opposite judgments can be simultaneously false, because between them, denoting some extreme options, there is always a third, middle, intermediate option. If this middle case is true, then the two extremes will be false. Between opposing (extreme) judgments: “ All people are truthful ,” “ All people are not true ,” is the third, middle option: “ Some people are truthful, and some are not ,” which, being a true judgment, determines simultaneous falsity of two extreme, opposite judgments.
2. Contradiction (kontradiktornost) - is the relationship between two judgments, in which the predicates are the same, the bundles are different, and the subjects differ in their volumes, that is, they are in relation to subordination (type and gender). For example, the judgments: “ All people are truthful,” “Some people are not true ,” are in contradiction. An important sign of contradictory judgments, as opposed to opposite ones, is that there can be no third, middle, or intermediate variant between them. By virtue of this, two contradictory judgments cannot be simultaneously true and cannot be simultaneously false: the truth of one of them necessarily means the falsity of the other, and vice versa - the falsity of one determines the truth of the other. We will return to opposite and contradictory judgments when it comes to the logical laws of contradiction and the excluded third.
The considered relations between simple comparable judgments are depicted schematically with the help of a logical square (Fig. 32), which was developed by medieval logicians:
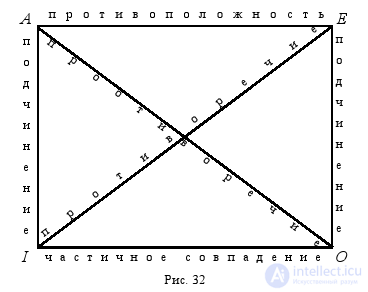
The vertices of the square denote four kinds of simple judgments, and its sides and diagonals - the relationship between them. Thus, the judgments of type A and type I , as well as the judgments of type E and type O are in respect of subordination. Judgments of type A and type E are in the relation of opposition, while judgments of type I and type O are of partial coincidence. Judgments of type A and type O , as well as judgments of type E and type I, are in contradiction. It is not surprising that a logical square does not depict an equivalence relation, because there are similar judgments in this respect, that is, equivalence is a relationship between judgments A and A , I and I , E and E , O and O. To establish the relationship between two judgments, it suffices to determine which type each of them relates to. For example, it is necessary to find out in what relation the judgments are: “ All people studied logic ”, “ Some people did not study logic ”. Seeing that the first proposition is general-affirmative ( A ), and the second one is partial negative ( O ), we can easily establish the relation between them using a logical square — a contradiction. Judgments: “ All people studied logic (A) ”, “ Some people studied logic (I) ”, are in relation to subordination, and judgments: “ All people studied logic (A) ”, “ All people did not study logic (E) ” Are in relation to the opposite.
As already mentioned, an important property of judgments, as opposed to concepts, is that they can be true or false.
As for comparable judgments, the truth values of each of them are in a certain way related to the truth values of the others. So, if a judgment of the form A is true or false, then the other three ( I , E , O ) comparable judgments (having similar subjects and predicates), depending on this (on the truth or falsehood of the opinion A ) are true or false. For example, if a judgment of the form A : “ All tigers are predators ” is true, then the judgment of type I : “ Some tigers are predators ” is also true (if all tigers are predators, then some of them are . e. Some tigers are predators too), the judgment of type E : “ All tigers are not predators ,” is false, and the judgment of type O : “ Some tigers are not predators, ” is also false. Thus, in this case, the truth of a judgment of type A implies the truth of a judgment of type I and the fallacy of judgments of type E and type O (of course, we are talking about comparable judgments, that is, having the same subjects and predicates).
1. Which judgments are called comparable and which are incomparable?
2. What are compatible and incompatible judgments? Give three examples of compatible and incompatible judgments.
3. In what ways can there be compatible judgments? Give two examples of equivalence, subordination, and partial coincidence.
4. In what ways can there be incompatible judgments?
Give three examples for the relationship of opposites and contradictions. Why can opposite judgments be simultaneously false, and contradictory cannot?
5. What is a logical square? How does he portray the relationship between judgments? Why doesn't a logical square represent an equivalence relation? How to determine the relationship between two simple comparable judgments using a logical square?
6. Take any true or false judgments of type A and draw conclusions from it about the truth of comparable judgments of types E , I , O. Take any true or false judgments of the form E and draw conclusions from it about the truth of the judgments A , I , O comparable with it.
Comments
To leave a comment
Logics
Terms: Logics