Lecture
In the previous article We considered issues related to the coding and transmission of information via a communication channel in the ideal case, when the process of transmitting information is carried out without errors. In fact, this process is inevitably accompanied by errors (distortions). A transmission channel in which distortion is possible is called a channel with noise (or noise). In the particular case of errors occur in the process of coding itself, and then the encoder can be considered as a channel with interference.
It is obvious that the presence of interference leads to loss of information. In order to receive the required amount of information on the receiver in the presence of interference, it is necessary to take special measures. One such measure is the introduction of so-called “redundancy” in the transmitted messages; at the same time, the source of information delivers obviously more characters than would be necessary in the absence of interference. One form of redundancy is simply repeating a message. This technique is used, for example, when hearing is poor on the phone, repeating each message twice. Another well-known way to increase the reliability of transmission is to transmit the word “by letter” - when instead of each letter a well-known word (name) is transmitted, starting with this letter.
Note that all living languages naturally have some redundancy. This redundancy often helps to restore the correct text "within the meaning of" the message. That is why the distortion of individual letters of telegrams, which are often found, quite rarely leads to a real loss of information: it is usually possible to correct a distorted word using the properties of the language alone. It would not be in the absence of redundancy. A measure of the redundancy of the language is the value
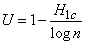 , (18.9.1)
, (18.9.1)
Where 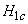 - the average actual entropy per one transmitted character (letter), calculated for fairly long passages of text, taking into account the dependence between the characters,
- the average actual entropy per one transmitted character (letter), calculated for fairly long passages of text, taking into account the dependence between the characters, 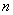 - the number of characters (letters) used,
- the number of characters (letters) used, 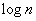 - the maximum possible in these conditions, the entropy on one transmitted symbol, which would be if all the symbols were equally probable and independent.
- the maximum possible in these conditions, the entropy on one transmitted symbol, which would be if all the symbols were equally probable and independent.
Calculations made on the material of the most common European languages show that their redundancy reaches 50% or more (that is, roughly speaking, 50% of the transmitted characters are redundant and could not be transferred if not for the danger of distortion).
However, for the accurate transmission of information, the natural redundancy of the language may be both excessive and insufficient: it all depends on how great the danger of distortion (“interference level”) in the communication channel is.
Using information theory methods, it is possible to find the necessary degree of information source redundancy for each interference level. The same methods help develop special error-correcting codes (in particular, the so-called "self-correcting" codes). To solve these problems, you must be able to take into account the loss of information in the channel associated with the presence of interference.
Consider a complex system consisting of a source of information 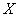 communication channel
communication channel 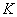 and receiver
and receiver 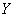 (fig. 18.9.1).
(fig. 18.9.1).
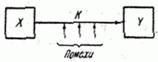
Fig. 18.9.1.
The source of information is a physical system. 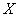 , which has
, which has 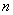 possible states
possible states
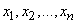
with probabilities
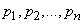 .
.
We will consider these states as elementary symbols that the source can transmit. 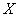 through the channel
through the channel 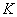 to receiver
to receiver 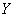 . The amount of information per character that the source gives will be equal to the entropy per character:
. The amount of information per character that the source gives will be equal to the entropy per character:
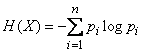 .
.
If the message transfer was not accompanied by errors, then the amount of information contained in the system 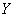 regarding
regarding 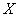 , it would be equal to the very entropy of the system
, it would be equal to the very entropy of the system 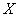 . If there are errors, it will be less:
. If there are errors, it will be less:
 .
.
It is natural to consider conditional entropy. 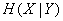 as the loss of information on one elementary symbol associated with the presence of interference.
as the loss of information on one elementary symbol associated with the presence of interference.
Knowing how to determine the loss of information in a channel per one elementary symbol transmitted by a source of information, it is possible to determine the channel capacity with interference, i.e., the maximum amount of information that a channel is capable of transmitting per unit of time.
Suppose a channel can transmit in unit time 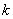 elementary characters. In the absence of interference, the channel capacity would be equal to
elementary characters. In the absence of interference, the channel capacity would be equal to
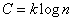 , (18.9.2)
, (18.9.2)
since the maximum amount of information that a single character can contain is 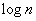 and the maximum amount of information that can contain
and the maximum amount of information that can contain 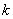 characters equal to
characters equal to 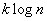 and it is achieved when the symbols appear independently from each other.
and it is achieved when the symbols appear independently from each other.
Now consider the channel with interference. Its capacity is defined as
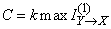 , (18.9.3)
, (18.9.3)
Where 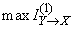 - maximum information per symbol that a channel can transmit in the presence of interference.
- maximum information per symbol that a channel can transmit in the presence of interference.
The determination of this maximum information in the general case is a rather complicated matter, since it depends on how and with what probabilities the symbols are distorted; is there any confusion, or is it just a loss of some characters; Does the character distortion occur independently of each other, etc.?
However, for the simplest cases, the channel capacity can be calculated relatively easily.
Consider, for example, such a task. Link  transmits from the source of information
transmits from the source of information 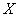 to receiver
to receiver 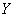 elementary symbols 0 and 1 in number
elementary symbols 0 and 1 in number 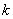 characters per unit of time. In the process of transferring each character, independently of the others, with probability
characters per unit of time. In the process of transferring each character, independently of the others, with probability 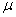 may be distorted (i.e. replaced by the opposite). Required to find the bandwidth.
may be distorted (i.e. replaced by the opposite). Required to find the bandwidth.
We first determine the maximum information per symbol that a channel can transmit. Let the source produce characters 0 and 1 with probabilities 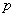 and
and 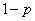 .
.
Then the source entropy will be
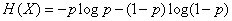 .
.
Define information 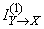 on one elementary character:
on one elementary character:
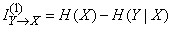 .
.
To find complete conditional entropy 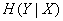 first we find the partial conditional entropies:
first we find the partial conditional entropies: 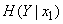 (system entropy
(system entropy 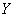 provided that the system
provided that the system 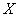 took the state
took the state 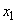 ) and
) and 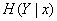 (system entropy
(system entropy 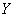 provided that the system
provided that the system 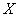 took the state
took the state 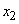 ). Calculate
). Calculate 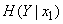 , for this we assume that an elementary symbol 0 is transmitted. We will find the conditional probabilities that the system
, for this we assume that an elementary symbol 0 is transmitted. We will find the conditional probabilities that the system 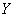 is able to
is able to  and able
and able 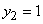 . The first one is equal to the probability that the signal is not confused:
. The first one is equal to the probability that the signal is not confused:
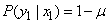 ;
;
the second is the probability that the signal is confused:
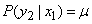 .
.
Conditional entropy 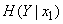 will be:
will be:
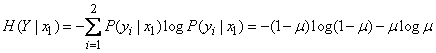 .
.
We now find the conditional entropy of the system. 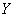 provided that
provided that 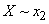 (signal unit is transmitted):
(signal unit is transmitted):
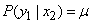 ;
; 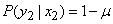 ,
,
from where
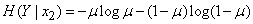 .
.
In this way,
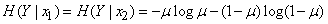 . (18.9.4)
. (18.9.4)
Total conditional entropy 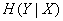 it turns out if we average the conditional entropies
it turns out if we average the conditional entropies 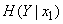 and
and 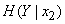 taking into account the probabilities
taking into account the probabilities 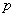 and
and 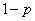 values
values 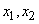 . Since the partial conditional entropies are equal,
. Since the partial conditional entropies are equal,
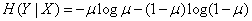 .
.
We got the following conclusion: conditional entropy 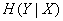 does not depend on what probabilities
does not depend on what probabilities 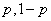 there are 0 characters; 1 in the transmitted message, and depends only on the probability of error
there are 0 characters; 1 in the transmitted message, and depends only on the probability of error 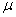 .
.
We calculate the complete information transmitted by one symbol:
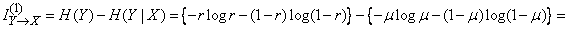
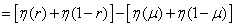 ,
,
Where 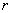 - the probability that the symbol 0 will appear at the output. Obviously, with the given channel properties, the information for one symbol
- the probability that the symbol 0 will appear at the output. Obviously, with the given channel properties, the information for one symbol 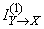 peaks when
peaks when 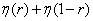 as much as possible. We know that such a function reaches its maximum when
as much as possible. We know that such a function reaches its maximum when  i.e. when on the receiver both signals are equally probable. It is easy to see that this is achieved when the source transmits both symbols with the same probability.
i.e. when on the receiver both signals are equally probable. It is easy to see that this is achieved when the source transmits both symbols with the same probability. 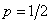 . With the same meaning
. With the same meaning 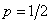 reaches the maximum and information on one character. The maximum value is
reaches the maximum and information on one character. The maximum value is
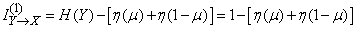 .
.
Therefore, in our case
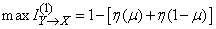 ,
,
and the bandwidth of the communication channel will be equal to
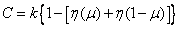 . (18.9.5)
. (18.9.5)
notice, that 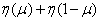 is nothing but the entropy of a system that has two possible states with probabilities
is nothing but the entropy of a system that has two possible states with probabilities 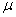 and
and 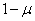 . It characterizes the loss of information on a single character associated with the presence of interference in the channel.
. It characterizes the loss of information on a single character associated with the presence of interference in the channel.
Example. 1. Determine the bandwidth of a communication channel capable of transmitting 100 symbols 0 or 1 per unit of time, each of the symbols being distorted (replaced by the opposite) with probability 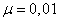 .
.
Decision. According to table 7 of the application we find
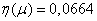 ,
,
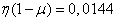 ,
,
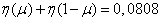 .
.
Information per one symbol is lost 0.0808 (two units). Bandwidth is equal to
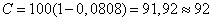
binary units per unit of time.
With the help of similar calculations, the channel capacity can also be determined in more complex cases: when the number of elementary symbols is more than two and when the distortions of individual symbols are dependent. Knowing the capacity of the channel, you can determine the upper limit of the speed of transmission of information on the channel with interference. We formulate (without proof) the second Shannon theorem relating to this case.
2nd theorem of Shannon
Let there is a source of information 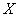 , the entropy of which is equal per unit of time
, the entropy of which is equal per unit of time 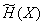 , and the channel with bandwidth
, and the channel with bandwidth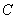 . Then if
. Then if
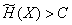 ,
,
then, with any coding, the transmission of messages without delays and distortions is impossible. If
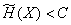 ,
,
it is always possible to encode a sufficiently long message so that it is transmitted without delays and distortions with a probability arbitrarily close to one.
Example 2. There is a source of information with entropy per unit of time 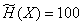 (two units) and two communication channels; each of them can transfer 70 binary characters (0 or 1) per unit of time; each binary sign is replaced by the opposite with probability
(two units) and two communication channels; each of them can transfer 70 binary characters (0 or 1) per unit of time; each binary sign is replaced by the opposite with probability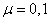 . It is required to find out: is the bandwidth of these channels sufficient to transmit information supplied by the source?
. It is required to find out: is the bandwidth of these channels sufficient to transmit information supplied by the source?
Decision. Determine the loss of information on one character:
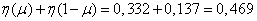 (two units).
(two units).
The maximum amount of information transmitted over one channel per unit of time:
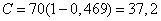 .
.
The maximum amount of information that can be transmitted on two channels per unit of time:
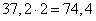 (two units),
(two units),
which is not enough to ensure the transfer of information from the source.
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory