General concepts and elements of coding theory.

Lecture 4 .

4 1 General concepts and elements of coding theory.

We define some concepts.

Encoding is the operation of identifying characters or groups of characters of one code with groups of characters of another code.

A code is a set of characters and a system of certain rules by which information can be presented or encoded as a set of these characters for transmission, processing and storage. The final sequence of code points is called a word. Most often , the letters, numbers, symbols and their combinations are used to encode information .

Consider a generalized scheme for transmitting digital information.

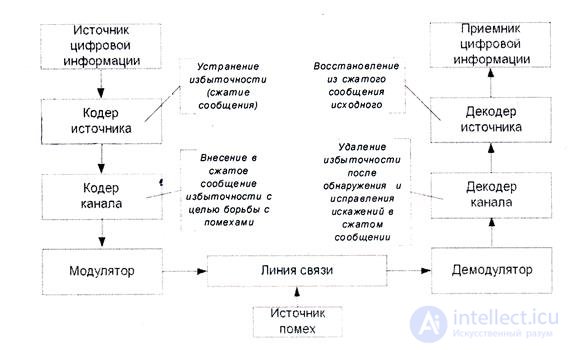
Fig.4.1 Generalized scheme of transferring digital information

The principles of information coding considered today are valid both for systems whose main task is the transfer of information in space (communication systems), and for systems whose main task is the transfer of information in time (information storage systems).

The input of the source coder receives a sequence of characters included in the set, called the primary alphabet .

The coder converts this sequence into another one, most often composed of other characters, the set of which forms the secondary alphabet .

If encoding-decoding operations are performed by a computer and an intermediate presentation of information to a person is not required, these alphabets most often consist of 2 characters — 0 and 1. This is due to the peculiarities of modern digital devices and their element base.

Since the volume or number of characters of the secondary alphabet is less than the volume of characters of the primary alphabet, when encoding each character or group of characters of the primary alphabet, the group of characters of the secondary alphabet, which is called a code combination, is assigned . The number of characters in the secondary alphabet in a code combination is called its length.

Codes whose secondary alphabet consists of two characters, usually 0 and 1, are called binary.

The operation of forming a sequence of code combinations from an input sequence of characters or combinations of the primary alphabet is called coding. Encoding is performed using an encoder, which can be a device, a program, or a hardware-software complex .

The reverse operation is called decoding and is performed by the decoder .

4 2 Coding objectives .

The decisive contribution to the theory of information transfer in the late 40s, as is well known, was made by the American scientist Claude Shannon. He substantiated, in particular, the effectiveness of the input into the information transfer system of encoding-decoding devices, the main purpose of which is to harmonize the information properties of the message source with the properties of the communication channel.

One of them, the source coder, provides such coding, in which, by eliminating redundancy, the amount of data transmitted over the communication channel is significantly reduced.

Such coding is called effective or optimal.

If interference occurs in the communication channel, this coding converts the data into a form suitable for subsequent error-correcting coding.

Anti-noise coding is performed by a channel coder. Its meaning follows from the name - the fight against distortions arising due to interference acting in the communication channel.

Thus, using a source encoder based on the statistical characteristics of the encoded message, its volume is reduced, and using a channel encoder based on statistical characteristics operating in the interference channel, data transmitted through the channel can be recovered , even if they are distorted.

This separation greatly simplifies the study and design of codecs.

In the case of low redundancy, you can refuse to use the source codec decoder. At low intensity of interference in the communication channel, it is possible to refuse the noise-resistant coding and, accordingly, from the channel coder-decoder.

Elements of Coding Theory

Some common properties of codes .

Consider the examples. Suppose that a discrete source, issuing at the output of a message, has an alphabet of N letters or symbols, arriving with probabilities p 1 , p 2 , ..., p N.

Each character is encoded using a secondary alphabet of m letters. Denote n i - the number of letters in a code word that corresponds to the i- th letter of the source. We will be interested in the average length of the code word n sr , which is found by the well-known formula:

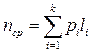
As an example, we consider possible ways of composing binary code code words with the volume of the primary alphabet k = 4

Table 4.1

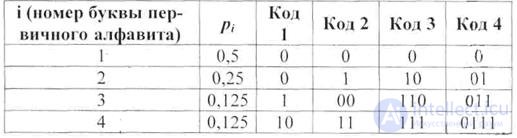
Note that code 1 has an unsuccessful property, consisting in the fact that letters with numbers 1 and 2 are encoded in the same way - code word 0. Therefore, unambiguous decoding using this code is impossible.

Code 2 has a similar disadvantage: the sequence of the two second letters of the primary source is encoded in 00, which is the same as the code word for the letter 3. In this case, there will not be any difficulties for decoding if there is any separator between the code words symbol. But if such a character is entered, it can be understood as an additional letter of the secondary alphabet. Then each code word at the end or at the beginning is simply complemented by this letter. As a result, such a code can be considered as a special case of codes without separating characters. For this reason, codes with separators are not considered separately .

An example of such a code is code 4, where 0 can be understood as a separator character.

It follows from the above that the code is uniquely decoded if the code words corresponding to the different letters of the primary alphabet are different. This is a necessary condition for unambiguous decodability, but not always sufficient.

==================================

From the point of view of theory and practice, the so-called prefix codes are the most important among all the uniquely decoded codes.

Prefix codes are codes in which each codeword is not the initial part or prefix of another codeword. This is already a sufficient condition for unambiguous decodability.

It is easy to see that codes 1 and 2 are not prefix.

Questions for students:

1) Are codes 3 and 4 prefix?

2) Are codes 3 and 4 uniquely decodable?

Codes are conveniently described graphically using a graph called a code tree. This tree is built from one vertex and has nodes of zero, first, second, etc. orders. From each node there are m rays - edges, each of which corresponds to a certain letter of the secondary alphabet.

In fig. 4.2. shows the code tree of code 3, described in table 4.1.

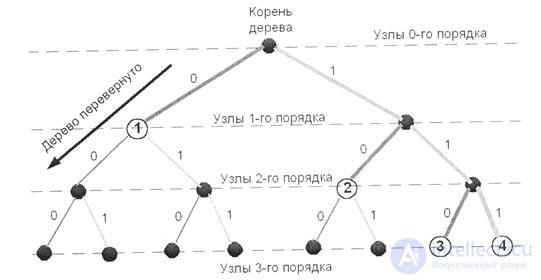
Fig. 4.2.

Each i-th code word of length n i is assigned a node x i , of the i-th order and a specific path through the code tree from the root to this node.

From the graphical representation it follows that the code will be prefix if the nodes corresponding to the code words are terminal, i.e. through them does not lie the path to the other nodes, also corresponding to the code words.

4 3 Optimal non-uniform codes.

Definitions

Uneven call codes whose code words have different lengths.

The optimality can be understood in different ways, depending on the criterion. In this case, this criterion is the average length of the code word. The optimality with regard to this criterion is understood in the sense of the minimum length of the average length of the code word.

Further conclusions will be made under the following conditions:

Let the letters of the primary source a 1 a 2. , .., and k have the probabilities of occurrence p 1 , p 2 , ..., p k . Let us arrange the letters in decreasing order of the probabilities of their appearance in the message and enumerate them in that order. As a result, p 1 > p 2 > ...> p k . For coding, we will use a secondary alphabet consisting of 2 letters - 0 and 1, i.e. binary code

Let x 1 , x 2 , ..., x k be the set of code words having length n 1 , n 2 , ..., n k . We restrict ourselves to considering only prefix codes. The results obtained for the lengths of code words for prefix codes can be distributed to the whole class of uniquely decoded codes, and the results obtained for binary codes can be generalized to codes with any size of the secondary alphabet.

4.4 Shannon-Feno codes.

Independently, Shannon and Feno proposed a procedure for building efficient code. The code obtained with its power is called the Shannon-Feno code.

The Shannon-Feno code is constructed as follows:

1) letters of the alphabet of messages are written out in the table in decreasing order of probabilities;

2) then they are divided into two groups so that the sums of probabilities in each of the groups are as equal as possible;

3) all letters of the upper half are assigned 1 as the first symbol, and all lower letters are given the symbol 0;

4) each of the obtained groups, in turn, is divided into two subgroups with the same total probabilities, and so on;

5) the process is repeated until one letter remains in each subgroup.

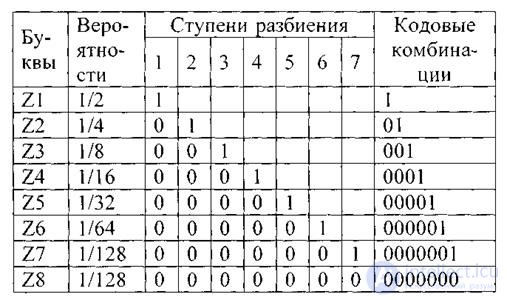
Consider a primary source of eight characters. It is clear that with normal (non-statistical) encoding , three characters are required to represent each letter. Let the probabilities of occurrence of letters of the primary source are equal:

p 1 = 1/2; p 2 = 1/4; p 3 = 1/8; p 4 = 1/16; p 5 = 1/32; p == 1/64; p 7 = 1/128; p 8 = 1/128 /

The greatest compression effect is obtained when the probabilities of the letters are negative integer powers of two. The average number of characters per letter in this case is exactly equal to the entropy.

Let us verify this by calculating the entropy for our example:

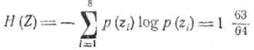
and the average number of characters per letter of the primary alphabet.

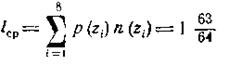
where n (z i ) is the number of characters in the code combination corresponding to the letter z i . The characteristics of such an ensemble and the codes of the letters are presented in Table 4.2.

Table 4.2.

More generally, for an eight-letter alphabet, the average number of characters per letter will be less than three, but greater than the entropy of the alphabet H (Z). For an ensemble of letters given in the following table for another source, the entropy is 2.76, and the average number of characters per letter is 2.84.

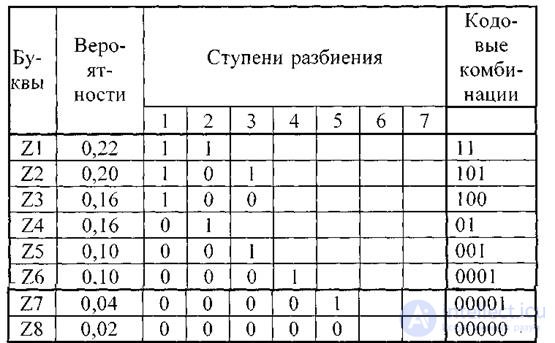
Table 4.3.

Consequently, some redundancy in the sequences of characters remained. From the theorem of Shannon, it follows that this redundancy can also be reduced if we proceed to coding with sufficiently large blocks.

Consider messages formed with the help of an alphabet consisting of only two letters Z 1 and Z 2 , with the probabilities of occurrence of p (Z 1 ) = 0.9 and p (Z 2 ) = 0.1, respectively .

Since the probabilities are not equal, a sequence of such letters will have redundancy. However, with the literal coding of Shannon-Fano, no effect is obtained.

Indeed, the transmission of each letter requires either a 1 or 0 character, and n cf. = 1 while entropy is 0.47.

When coding blocks containing two letters each, we get the codes shown in the table.

Table 4.4.

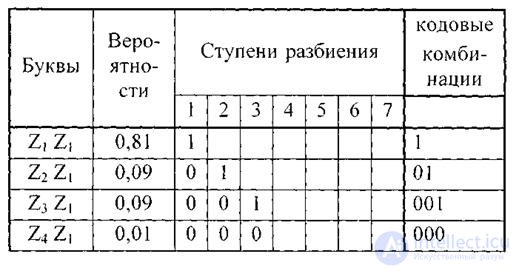
Since the letters are not statistically related, the probabilities of the blocks are defined as the product of the probabilities of the constituent letters.

The average number of characters per block is 1.29; and on a letter-0,645.

Encoding blocks of three letters each gives even greater effect. The corresponding ensemble and codes are listed in the table.

Table 4.5.

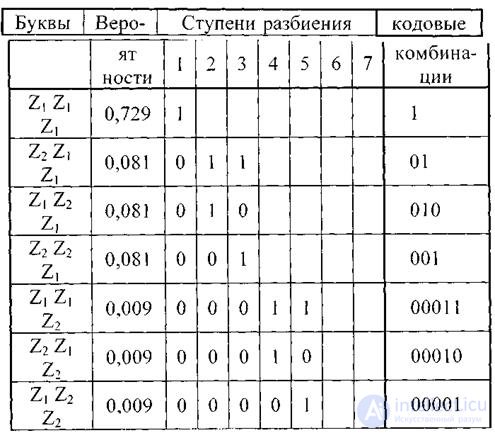
The average number of characters per block is 1.59; and on a letter - 0,53; which is only 12% more entropy. The theoretical minimum H (Z) = 0.47 can be achieved by coding blocks that include an infinite number of letters:

lim l cp = H (Z), as m → ∞

It should be emphasized that the increase in coding efficiency with block escalation is not related to the more distant statistical links, since we considered alphabets with uncorrelated letters. The increase in efficiency is determined only by the fact that the set of probabilities, resulting from the enlargement of blocks, can be divided into subgroups that are closer in total probabilities.

The Shannon – Feno method considered by us does not always lead to a unique code construction. In the method there is an element of subjectivism. After all, when divided into subgroups, it is possible to make both the upper and lower subgroups more likely.

Therefore, the specific code received may not be the best. When constructing efficient codes with base m> 2, the uncertainty of division into groups becomes even greater.

From this drawback free method Huffman. It guarantees an unambiguous construction of the code with the lowest average number of characters per letter for a given probability distribution .

4.5 Huffman Codes.

The algorithm for constructing the optimal code proposed by Huffman in 1952 is built on this algorithm:

1) letters of the primary alphabet are written out in the main column in decreasing order of probabilities;

2) the last two letters are combined into one auxiliary letter to which the total probability is attributed;

3) the probabilities of letters that did not participate in the union, and the resulting total probability is again arranged in decreasing order of probabilities in the additional column, and the last two are combined;

3) the process continues until we receive a single auxiliary letter with a probability equal to one.

The technique is illustrated by example.

Table 4.6

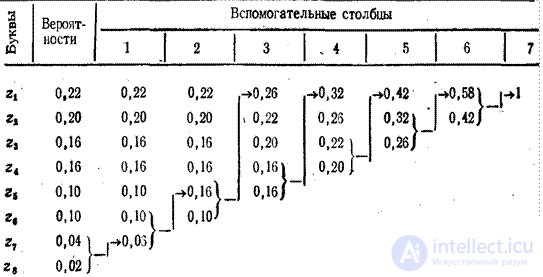
In order to compose a code combination corresponding to a specific symbol, one should trace the path of transition of the probability of a symbol by rows and columns of the table.

For clarity, when building a code code tree is built. From the point corresponding to probability 1, two branches are sent, and the branches are more likely to be assigned the symbol 1, and with the lesser - 0. This sequential branching is continued until we reach each letter. The code tree for the alphabet of letters considered in the table is shown in Figure 4.2.

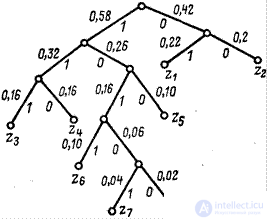
Fig.4.3

Now, moving from top to bottom through the code tree, we can write the corresponding code combination for each letter (see table 4.7).

Table 4.7

Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8
01	00	111	110	100	1011	10101	10,100

4.6 Features of effective codes.

1. The letter of the primary alphabet with the smallest probability of occurrence is put into correspondence with the code with the greatest length, i.e. such code is uneven (with different length of code words). As a result, if the receiver cannot control the transmission of a message from a source (for example, code words arrive strictly periodically in increments of ∆t ), code words with different length, i.e. the number of letters of the secondary alphabet transmitted per unit of time through the communication line will vary. Taking into account the fact that any communication line is characterized by the maximum information transfer speed (throughput), we conclude that using such a data transmission scheme, the transmission capacity of the communication line will not be fully utilized. To avoid the inefficient use of the communication line is possible by installing buffer storage memories at its input and output. They make it possible to smooth out the irregularity of the letters of the secondary alphabet both through the communication line and at the input of the decoder. In this case, there are time delays in the entire information transmission system, and the higher the buffer device volume, the higher these delays.

2. The second feature is associated with time delays in the transmission of information arising from the use of coding blocks of letters of the primary alphabet, which allow to increase the efficiency of the code (to reduce the average length of the code word). Coding blocks of letters of the primary alphabet requires their prior accumulation. Hence the temporary delays that arise .

3. The third feature is that, as it turns out, effective codes are not intended for use in interference conditions. If , nevertheless, for some reason, for example, as a result of electrical interference from a lightning discharge, some character of the code word is distorted, correct decoding becomes impossible not only for this code word, but also for a number of subsequent codecs. of words.

There is a so-called error track. Thus, improving one of the quality characteristics of the code, in this case, the average length of the code word n sr , another characteristic is deteriorating - its resistance to interference. Effective codes should be used either in conditions of complete absence of interference, or to eliminate redundancy of the message and preparation with subsequent error- correcting coding.

4.7 Test questions.

1. What is coding?

2. Why encode information?

3. What are the basic requirements for codes.

4. What is the optimal non-uniform code?

5. What is the main difference between the Huffman coding method and the Shannon-Fano method?

Topic 4. Encoding of the source of discrete messages in the channel with interference. General principles of robust coding.