Lecture
Information theory is one of the courses in training information systems, automated systems for managing and processing information. The functioning of such systems is essentially related to obtaining, preparing, transmitting, storing and processing information, because without the implementation of these steps it is impossible to make the right decision, which is the ultimate goal of any system.
The emergence of the theory of information is usually associated with the emergence of the fundamental work of the American scientist K. Shannon "Mathematical theory of communication" (1948). However, the results obtained by other scientists were also organically integrated into information theory. For example, R. Hartley, first proposed a quantitative measure of information (1928), a Soviet academician. A. Kotelnikov, formulated the most important theorem on the possibility of representing a continuous function as a set of its values at individual points of reference (1933) and developed optimal methods for receiving signals against interference.
To the theory of information, in its classical statement, include the following questions:
I-analysis of the assessment of the "amount of information".
II- analysis of the information characteristics of communication communications communication sources;
III- substantiation of the basic possibility of encoding and decoding messages.
IV- determination of the potential characteristics of the transmission rate of messages over the communication channel, both in the absence and in the presence of interference.
If one considers the problems of developing specific methods and means of coding messages, then the totality of the questions posed is called information theory and coding or applied information theory.
Attempts to widely use the ideas of information theory in various fields of science are related to the fact that this theory is basically mathematical. Its basic concepts (entropy, amount of information, bandwidth) are determined only through the probabilities of events to which the most diverse physical content can be attributed. The approach to research in other areas of science from the standpoint of using the basic ideas of information theory has been called the theoretical information approach. Its application in a number of cases allowed obtaining new theoretical results and valuable practical recommendations. However, this approach often leads to the creation of process models that are far from adequate to reality. Therefore, in any research that goes beyond the purely technical problems of transmitting and storing messages, information theory should be used with great caution. Especially it concerns the modeling of human mental activity, the processes of perception, evaluation and processing of information by him.
The content of the lecture notes is limited to the consideration of the questions of the theory and practice of coding in its narrow technical sense.
The concept of information.
What is information? Since the early 1950s, attempts have been made to use the concept of information (which has not yet had a single definition) to explain and describe a wide variety of phenomena and processes.
Some textbooks provide the following definition of information:
Information is a collection of information to be stored, transmitted, processed.
Such a definition helps even vaguely to imagine what is at stake. But from the point of view of logic, it is meaningless. The defined concept (information) here is replaced by another concept (set of information), which itself needs to be defined.
With all the differences in the interpretation of the concept of information, it is indisputable that the information always manifests itself in the material and energy form in the form of signals during transmission, reception and storage of data.
The following stages of information circulation can be distinguished:
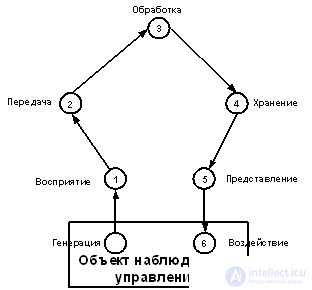
Figure 1.1 Stages of handling information
At the stage of information processing, purposeful extraction and analysis of information about an object (process) is carried out, as a result of which an image of an object is formed, its identification and assessment is carried out. At the same time, the information of interest is separated from noise and interference.
At the stage of information preparation, a signal is received in a form convenient for transmission or processing (normalization, analog-digital conversion, etc.).
At the stage of transmission and storage, information is sent either from one place to another, or from one point in time to another (information storage)
At the stage of information processing, its general and essential interdependencies for the selection of control actions (decision making) are highlighted.
At the stage of displaying information, it is presented to a person in a form capable of influencing his senses.
During the impact phase, information is used to make the necessary changes in the system.
Information enters the system in the form of messages. Under the message understand the set of characters or primary signals containing information.
The source of the message in the general case forms the totality of the source of information (AI) (the object under study or observed) and the primary transducer (PP) (sensor, human operator, etc.) that perceives information about the process occurring in it.
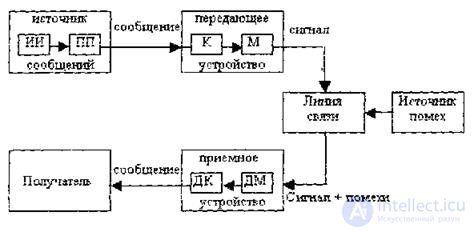
Fig. 1.2 Structural scheme of a single channel information transfer system.
There are discrete and continuous messages.
Discrete messages are formed as a result of the sequential issuance of messages by the source of individual elements - characters or symbols.
Many different characters are called the alphabet of the message source, and the number of characters - the volume of the alphabet.
Continuous messages are not divided into elements. They are described by continuous functions of time that take a continuous set of values (speech, television image). We will consider only some aspects of the information characteristics of continuous message sources to determine the potential of message sources and transmission channels.
The conversion of a message into a signal convenient for transmission over a given communication channel is called coding in a broad sense of the word.
The operation of recovering a message from a received signal is called decoding.
When encoding a discrete source, as a rule, they resort to the operation of representing the original characters in another alphabet with a smaller number of characters, called symbols. In the designation of this operation uses the same term "coding", considered in the narrow sense. A device that performs such an operation is called an encoding or encoder. Since the alphabet of coder symbols is smaller than the alphabet of the original (primary) characters, each character corresponds to a certain sequence of characters, which is called a code combination.
For the operation of matching characters with characters of the original alphabet, the term "decoding" is used. The technical implementation of this operation is carried out by the decoder or decoder.
The transmitting device converts continuous messages or characters into signals suitable for passing through the communication line. At the same time, one or several parameters of the selected signal are changed in accordance with the transmitted information. This process is called modulation. It is carried out by the modulator. The inverse conversion of signals into symbols is performed by a demodulator. Under the line of communication understand the environment (air, metal, magnetic tape, etc.), providing the flow of signals from the transmitting device to the receiving device.
The signals at the output of the communication line may differ from the signals at its input (transmitted) due to attenuation, distortion and the effect of interference.
Interference is called any disturbing disturbances, both external and internal, causing deviation of the received signals from the transmitted signals.
From a mixture of a signal with interference, the receiving device extracts the signal and, by means of a decoder, restores the message, which in general can differ from the one sent. The measure of the correspondence of the received message to the sent message is called the fidelity of the transmission.
The received message from the output of the communication system arrives at the subscriber-recipient to whom the source information was addressed.
The combination of means intended for transferring messages, together with the transmission medium, is called a communication channel.
Information theory includes the following fundamental theoretical questions:
- analysis of the quantitative information characteristics of the sources of messages and communication channels.
- justification of the principal possibility of encoding and decoding messages that provide the maximum permissible transmission rate of messages over a communication channel, both in the absence and in the presence of interference.
Information theory explores information systems under clearly defined conditions:
1. The message source selects the Xi symbol from some set with a certain probability, Pi
2. Symbols can be transmitted over a communication channel in coded form. Coded messages form a set that is a one-to-one mapping of a set of characters. The decoding rule is known to the decoder (recorded in its program).
3. Symbols follow each other, and their number in the message can be arbitrarily large.
4. A message is considered as received correctly if, as a result of decoding, it can be exactly restored. It does not take into account how much time has passed since the message was transmitted until the end of decoding, and what the complexity of the encoding and decoding operations are.
5. The amount of information does not depend on the semantic content of the message, on its emotional impact, usefulness and even on its relation to reality.
As a basic characteristic of a message, information theory takes a quantity called the amount of information. This concept does not affect the meaning and importance of the transmitted message, but is related to the degree of uncertainty.
Let the source of random messages produce a total of N different characters or letters. Sometimes this character set is called the source alphabet. These characters or letters consist of messages at the source output. The length of an individual message is arbitrary, and may not be restricted at all.
We now introduce a measure of the uncertainty of the appearance of a certain symbol at the output of the source. It can be considered as a measure of the amount of information received when this symbol appears. The measure must satisfy a range of natural conditions. It should increase with an increase in the possibilities of choice, that is, with an increase in the number N of possible symbols at the output of the source. Then, for a measure of uncertainty, one could take the number of different symbols, assuming that they are equally probable.
Thus, let a message of arbitrary length, consisting of N different characters, appear at the output of a source of random messages. If all N source symbols are equally probable, then obtaining a particular symbol is equivalent to randomly selecting one of the N symbols with a probability of 1 / N.
It is clear that the more N, the greater the degree of uncertainty characterizes this choice and the more informative the message composed of these symbols can be considered.
Therefore, the number N could serve as a measure of the information content of the source.
However, this measure contradicts some intuitive notions. For example, when N = 1, when the uncertainty of the appearance of the symbol is absent, it would give an informative value equal to one. In addition, this measure does not meet the requirement of additivity, which is as follows. If two independent sources with the number of equally probable symbols N and Μ are considered as one source simultaneously implementing pairs of symbols N i M j , then it is natural to assume that the information content of the combined source should be equal to the sum of the informativity of the original sources. Since the total number of states of the combined source is ΝΜ , the required function must satisfy the condition
I (N, M) = I (N) + I (M)
Requirements are fulfilled if, as a measure of the informativeness of the source of messages with equal probabilities of occurrence of symbols, we take the logarithm of the number of different source symbols: Then with Ν = 1, I (U) = 0 and the additivity requirement for two or more sources is satisfied.
At the same time, as a measure of the uncertainty of choosing a SINGLE symbol from a source with equiprobable appearance of symbols, one takes the logarithm of the number of symbols of the source:
H = logN
This logarithmic function describes the amount of message source information. It is called entropy. This measure was proposed by the American scientist R. Hartley in 1928.
In principle, it does not matter what basis of the logarithm to use to determine the amount of information, since the transition from one base of the logarithm to another is reduced only to a change in the unit of measurement.
Since modern information technology is based on elements that have two stable states, the base of the logarithm is usually chosen to be two, i.e. information content is expressed as:
H = log 2 N.
Then a unit of information per one source symbol is called a binary unit or bit. In this case, the unit of uncertainty (binary unit or bit) is the uncertainty of the choice of two equally probable events (bit is the binary digit).
Since log 2 N = 1 should be N = 2, it is clear that one bit is the amount of information that characterizes a binary source with equiprobable symbols 0 and 1.
The binary message of such a source of length L contains L bits of information.
If the base of the logarithm is chosen to be ten, then the entropy is expressed in decimal units per message element — dit, with 1 bit = lg 2 bits = 3.32 bits.
Example. Determine the amount of information contained in the television signal corresponding to one scan frame. Let the frame have 625 lines, and the signal corresponding to one line is a sequence of 600 pulses of random amplitude, and the pulse amplitude can take any of 8 values in steps of 1 V.
Decision. In this case, the length of the message (symbol) corresponding to one line is equal to the number of pulses of random amplitude in it: n = 600.
The number of characters (different amplitude values) is equal to the number of values that the amplitude of pulses in a line can accept: N = 8.
Amount of information in one line : Isp. = 600 logN = 600 log 8 , and the amount of information in the frame: Isum = 625 * Isp = 625 * 600 log 8 == 1,125 • 10 6 bits
The above assessment of informativeness or entropy is based on the assumption that all characters of the alphabet are equally probable. In the general case, each of the symbols appears in the message source with different probabilities.
And now what i can do? How to characterize the information content or the measure of uncertainty of such a source? Consider ways to solve this problem.
Suppose, on the basis of statistical analysis, it is known that in a message of a sufficiently large length n, the sign Xi appears n; times i probability of occurrence of the sign xi
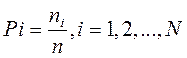
All signs of the alphabet of this source constitute a complete system of random events, therefore:
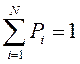
Let us introduce the concept of private entropy or uncertainty of the appearance of ONE specific i -th symbol of such a source:
H i = -log (P i )
Then, having weighed ALL partial entropies with the probabilities of their appearance P i , we can write expressions for the average entropy per ONE source symbol.
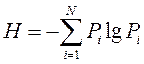
This average entropy characterizes to us ALL the source, its average entropy per symbol
This measure of entropy was introduced by Claude Shannon. It fully meets our intuitive requirements for a measure of information. It is additive, with probabilities of occurrence of source symbols equal to 1 and 0, it is also equal to 0 .
If the source message consists of n independent characters, then the total amount of information in this message
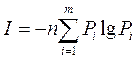
Further expressions for the amount of information I and entropy H always use logarithms with base 2,
If the alphabetic characters Pi = 1 / N are equally probable, the following formula is obtained from the Shannon formula:
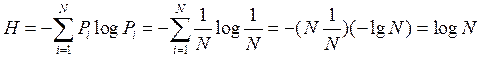
Из этого следует, что при равновероятности символовалфавита энтропия определяется исключительно числом символов алфавита и по существу является характеристикой только числа символов алфавита.
Если же знаки алфавита неравновероятны, то алфавит можно рассматривать как дискретную случайную величину, заданную статистическим распределением частот появления знаков X i (или вероятностей P i =n i / n ) табл. 1:1
Таблица 1.1
|
Символы X i |
X 1 |
X 2 |
... |
X m |
|
Вероятности P i |
P 1 |
P 2 |
... |
P m |
Такие распределения получают обычно на основе статистического анализа конкретных типов сообщений (например, русских или английских текстов и т.п.).
Поэтому, если знаки алфавита неравновероятны и хотя формально в выражение для энтропии входят вероятности появления его знаков, энтропия отражает статистические свойства некоторой совокупности сообщений.
Еще раз вернемся к понятию энтропии источника сообщений.
В выражении для энтропии
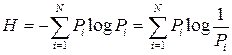
величина log 1/Pi представляет частную энтропию, характеризующую информативность знака х i , а энтропия Н - есть среднее значение частных энтропий. Таким образом, еще раз подчеркнем, что энтропия H источника выражает СРЕДНЮЮ энтропию на один символ алфавита.
Функция (Pi • log Pi) отражает вклад знака Xi в энтропию Н . При вероятности появления знака Pi=1 эта функция равна нулю, затем возрастает до своегомаксимума,апридальнейшем уменьшенииPiстремитсякнулю
Основные свойства энтропии
Энтропия Н - величина вещественная, неотрицательная и ограниченная, т.е. Н > 0 (это свойство следует из того, что такими же качествами обладают все ее слагаемые Pi log (1/Pi).
Энтропия равна нулю , если сообщение известно заранее (в этом случае каждый элемент сообщения замещается некоторым знаком с вероятностью, равной единице, а вероятности остальных знаков равны нулю).
Энтропия максимальна , если все знаки алфавита равновероятны, т.е. Нmах = log N.
Таким образом, степень неопределенности источника информации зависит не только от числа состояний, но и от вероятностей этих состояний. При неравновероятных состояниях свобода выбора источника ограничивается, что должно приводить к уменьшению неопределенности. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния. Действительно, в первом случае результат практически предрешен (реализация состояния, вероятность которого равна 0,99), а во втором случае неопределенность максимальна, поскольку никакого обоснованного предположения о результате выбора сделать нельзя. Ясно также, что весьма малое изменение вероятностей состояний вызывает соответственно незначительное изменение неопределенности выбора.
Особый интерес представляют бинарные источники, использующие алфавит из двух знаков: (0,1), При N = 2 сумма вероятностей знаков алфавита: P1+Р0 = 1. Можно положить P1 = Р, тогда Р0 = 1-Р.
Энтропию можно определить по формуле:
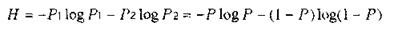
Энтропия бинарных сообщений достигаетмаксимального значения, равного 1 биту, когда знаки алфавита сообщении равновероятны, т.е. при Р 0,5 ее график симметричен относительно этого значения, (рис.3).
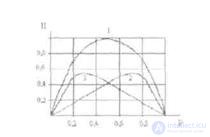
Fig. 1.3. График зависимости энтропии Н двоичных сообщений и ее составляющих : - (1 - Р) log (1 - Р) и - Р log P от Р .
ПримерЗаданы ансамбли X и Y двух дискретных величин
Таблица 1.2

Таблица 1.3.

Сравнить их энтропии.
Решение: Энтропия не зависит отконкретныхзначений случайной величины. Так как вероятности их появления в обоих случаях одинаковы, то
H (X) = H (Y) = ∑Pi * log (Pi) = - 4 (0,251og0.25) = -4 (l / 41ogl / 4) - = log 4 = 2 bits / s.
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory