Lecture
Let there be two systems 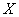 and
and 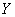 generally dependent. Suppose the system
generally dependent. Suppose the system 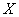 took the state
took the state 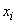 . Denote
. Denote 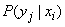 conditional probability that the system
conditional probability that the system 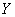 will take the state
will take the state 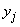 provided that the system
provided that the system 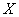 is able to
is able to 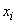 :
:
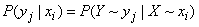 . (18.4.1)
. (18.4.1)
We now define the conditional entropy of the system 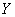 provided that the system
provided that the system 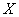 is able to
is able to 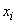 . Denote it
. Denote it 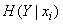 . By general definition, we have:
. By general definition, we have:
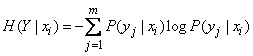 (18.4.2)
(18.4.2)
or
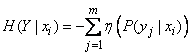 . (18.4.2 ')
. (18.4.2 ')
The formula (18.4.2) can also be written in the form of a mathematical expectation:
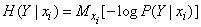 , (18.4.3)
, (18.4.3)
where is familiar 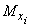 denotes the conditional expectation of the value in brackets, provided
denotes the conditional expectation of the value in brackets, provided 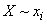 .
.
Conditional entropy depends on which state 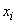 adopted the system
adopted the system 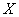 ; for some states, it will be more, for others - less. Determine the average, or total, entropy of the system
; for some states, it will be more, for others - less. Determine the average, or total, entropy of the system 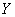 taking into account the fact that the system can take different states. To do this, each conditional entropy (18.4.2) must be multiplied by the probability of the corresponding state
taking into account the fact that the system can take different states. To do this, each conditional entropy (18.4.2) must be multiplied by the probability of the corresponding state 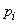 and all such works add up. Denote the full conditional entropy
and all such works add up. Denote the full conditional entropy 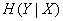 :
:
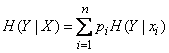 (18.4.4)
(18.4.4)
or, using the formula (18.4.2),
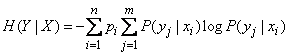 .
.
Bringing in 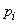 under the sign of the second sum, we get:
under the sign of the second sum, we get:
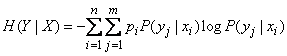 (18.4.5)
(18.4.5)
or
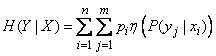 . (18.4.5 ')
. (18.4.5 ')
But by the probability multiplication theorem 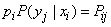 , Consequently,
, Consequently,
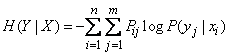 . (18.4.6)
. (18.4.6)
The expression (18.4.6) can also be given the form of a mathematical expectation:
 . (18.4.7)
. (18.4.7)
Magnitude 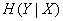 characterizes the degree of system uncertainty
characterizes the degree of system uncertainty 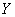 remaining after system state
remaining after system state 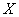 fully defined. We will call it the complete conditional entropy of the system.
fully defined. We will call it the complete conditional entropy of the system. 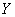 regarding
regarding 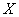 .
.
Example 1. There are two systems. 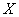 and
and 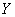 merged into one
merged into one 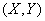 ; probabilities of system states
; probabilities of system states 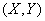 set by table
set by table
|
|
|
|
|
| 0.1 | 0.2 | 0 | 0.3 |
| 0 | 0.3 | 0 | 0.3 |
| 0 | 0.2 | 0.2 | 0.4 |
| 0.1 | 0.7 | 0.2 |
Determine the total conditional entropy 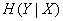 and
and 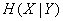 .
.
Decision. Adding probabilities 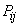 by columns, we get probabilities
by columns, we get probabilities 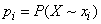 :
:
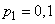 ;
; 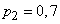 ;
; 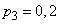 .
.
Write them in the bottom, extra row of the table. Similarly, folding 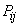 in rows, we find:
in rows, we find:
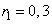 ;
; 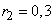 ;
; 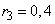
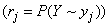
and write to the right an additional column. Sharing 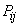 on
on 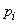 , we will receive the table of conditional probabilities
, we will receive the table of conditional probabilities 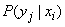 :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
By the formula (18.4.5 ') we find 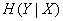 . Since the conditional entropy at
. Since the conditional entropy at 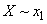 and
and 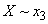 equal to zero then
equal to zero then
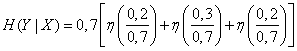 .
.
Using table 7 of the application, we find
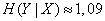 (two units).
(two units).
Similarly, we define 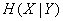 . From the formula (18.4.5 '), changing places
. From the formula (18.4.5 '), changing places 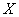 and
and 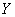 , we get:
, we get:
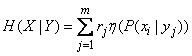 .
.
Make a table of conditional probabilities 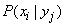 . Sharing
. Sharing 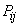 on
on 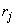 we will receive:
we will receive:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
From here
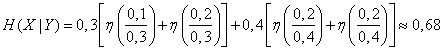 (two words).
(two words).
Using the concept of conditional entropy, one can determine the entropy of the combined system through the entropy of its constituent parts.
We prove the following theorem:
If two systems 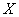 and
and 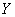 combined into one, the entropy of the combined system is equal to the entropy of one of its components plus the conditional entropy of the second part relative to the first:
combined into one, the entropy of the combined system is equal to the entropy of one of its components plus the conditional entropy of the second part relative to the first:
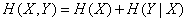 . (18.4.8)
. (18.4.8)
For proof, we write 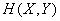 in the form of mathematical expectation (18.3.3):
in the form of mathematical expectation (18.3.3):
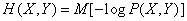 .
.
By the probability multiplication theorem
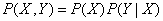 ,
,
Consequently,
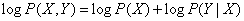 ,
,
from where
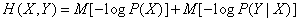
or, according to the formulas (18.2.11), (18.3.3)
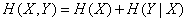 ,
,
Q.E.D.
In the particular case of systems 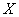 and
and 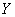 independent
independent 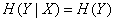 and we get the one already proven in the previous one
and we get the one already proven in the previous one  entropy addition theorem:
entropy addition theorem:
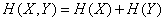 .
.
In general
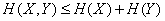 . (18.4.9)
. (18.4.9)
The ratio (18.4.9) follows from the fact that the total conditional entropy 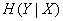 can not surpass the unconditional:
can not surpass the unconditional:
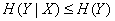 . (18.4.10)
. (18.4.10)
Inequality (18.4.10) will be proved in  18.6. Intuitively, it seems pretty obvious: it is clear that the degree of uncertainty of the system cannot increase because the state of some other system has become known.
18.6. Intuitively, it seems pretty obvious: it is clear that the degree of uncertainty of the system cannot increase because the state of some other system has become known.
It follows from relation (18.4.9) that the entropy of a complex system reaches a maximum in the extreme case when its components are independent.
Consider another extreme case where the state of one of the systems (for example 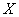 ) completely determines the state of another (
) completely determines the state of another ( 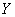 ). In this case
). In this case 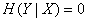 and the formula (18.4.7) gives
and the formula (18.4.7) gives
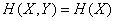 .
.
If the state of each system 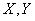 uniquely identifies the state of another (or, as they say, systems
uniquely identifies the state of another (or, as they say, systems 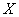 and
and 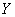 are equivalent)
are equivalent)
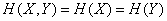 .
.
The entropy theorem of a complex system can be easily extended to any number of systems to be merged:
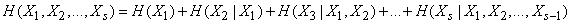 , (18.4.11)
, (18.4.11)
where the entropy of each subsequent system is calculated under the condition that the state of all the previous ones is known.
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory