Lecture
Previous 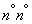 entropy was defined as a measure of the uncertainty of the state of a certain physical system. Obviously, as a result of obtaining information, the uncertainty of the system can be reduced. The greater the amount of information received, the more informative they are, the more information will be about the system, the less uncertain its state will be. Naturally, therefore, the amount of information measured by the decrease in the entropy of the system, to clarify the state of which information is intended.
entropy was defined as a measure of the uncertainty of the state of a certain physical system. Obviously, as a result of obtaining information, the uncertainty of the system can be reduced. The greater the amount of information received, the more informative they are, the more information will be about the system, the less uncertain its state will be. Naturally, therefore, the amount of information measured by the decrease in the entropy of the system, to clarify the state of which information is intended.
Consider some system  over which the observation is made, and evaluate the information obtained as a result of the fact that the state of the system
over which the observation is made, and evaluate the information obtained as a result of the fact that the state of the system  becomes completely famous. Prior to receiving information (a priori), the entropy of the system was
becomes completely famous. Prior to receiving information (a priori), the entropy of the system was 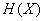 ; after receiving the information, the state of the system was completely determined, that is, the entropy became equal to zero. Denote
; after receiving the information, the state of the system was completely determined, that is, the entropy became equal to zero. Denote 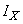 information obtained as a result of determining the state of the system
information obtained as a result of determining the state of the system  . It is equal to the decrease in entropy:
. It is equal to the decrease in entropy:
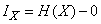
or
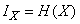 , (18.5.1)
, (18.5.1)
that is, the amount of information acquired when a state of a certain physical system is fully ascertained is equal to the entropy of this system.
Imagine the formula (18.5.1) in the form:
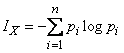 , (13.5.2)
, (13.5.2)
Where 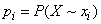 .
.
The formula (18.5.2) means that the information 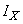 there is the logarithm of the state probability with the opposite sign, averaged over all system states.
there is the logarithm of the state probability with the opposite sign, averaged over all system states.
Indeed, to obtain 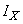 every value
every value 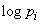 (logarithm of probability
(logarithm of probability 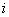 th state) with a minus sign multiplied by the probability of this state and all such works are added. Naturally every single addend -
th state) with a minus sign multiplied by the probability of this state and all such works are added. Naturally every single addend - 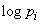 considered as private information received from a separate message, consisting in that the system
considered as private information received from a separate message, consisting in that the system  is able to
is able to 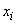 . Denote this information
. Denote this information 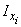 :
:
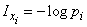 . (18.5.3)
. (18.5.3)
Then the information 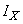 It will be presented as average (or complete) information received from all possible individual messages, taking into account their probabilities. Formula (18.5.2) can be rewritten in the form of mathematical expectation:
It will be presented as average (or complete) information received from all possible individual messages, taking into account their probabilities. Formula (18.5.2) can be rewritten in the form of mathematical expectation:
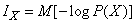 , (18.5.4)
, (18.5.4)
where is the letter  denotes any (random) system state
denotes any (random) system state  .
.
Since all the numbers 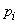 , not more than one, then both private information and complete
, not more than one, then both private information and complete 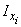 can not be negative.
can not be negative.
If all possible system states are a priori equally likely 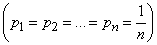 then naturally private information
then naturally private information 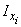 from each individual message
from each individual message

equal to the average (full) information
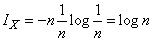 .
.
In the case when the system states have different probabilities, the information from different messages is not the same: the most information is carried by messages about those events that were a priori least likely. For example, the message that snow fell on December 31 in Moscow carries much less information than a message similar in content that snow fell on July 31 in Moscow.
Example 1. A piece is randomly placed on a chessboard in one of the cells. A priori, all positions of the piece on the board are equally likely. Determine the information received from the message in which particular cell the figure is located.
Decision. Entropy system  with
with 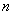 equiprobable states equals
equiprobable states equals 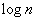 ; in this case
; in this case
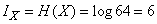 (two units),
(two units),
i.e. the message contains 6 binary units of information. Since all the states of the system are equally probable, any specific message of the type carries the same information: the figure is in the square e2.
Example 2. In the conditions of example 1, determine the private information from the message that the figure is in one of the corner cells of the board.
Decision. The prior probability of the reported state is
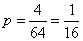 .
.
Private information is equal to
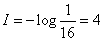 (two units).
(two units).
Example 3. Identify the private information contained in the message of the first person encountered  : "Today is my birthday".
: "Today is my birthday".
Decision. A priori, all days in a year are equally likely to be birthdays of a person 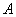 . Probability of received message
. Probability of received message 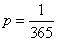 . Private information from this message
. Private information from this message
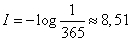 (two units).
(two units).
Example 4. In the conditions of example 3 to determine the full information from the message, figuring out whether today is the birthday of the first person met 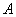 .
.
Decision. The system, the state of which is found out, has two possible states: 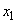 - birthday and
- birthday and 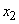 - not a birthday. Probabilities of these states
- not a birthday. Probabilities of these states 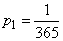 ;
; 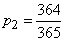 .
.
Full information is:
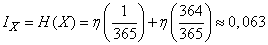 (two units).
(two units).
Example 5. A goal can be produced 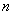 independent shots; the probability of hitting the target with each shot is equal
independent shots; the probability of hitting the target with each shot is equal 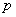 . After
. After 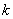 th shot
th shot 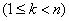 reconnaissance is done, informing whether the target is hit or not; if she is hit, she stops shooting. To determine
reconnaissance is done, informing whether the target is hit or not; if she is hit, she stops shooting. To determine 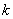 from the condition that the amount of information delivered by intelligence is maximum.
from the condition that the amount of information delivered by intelligence is maximum.
Decision. Consider the physical system 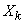 - target after
- target after 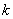 th shot. Possible system states
th shot. Possible system states 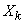 will be
will be
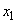 - the target is hit;
- the target is hit;
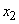 - The goal is not hit.
- The goal is not hit.
The probabilities of the states are given in the table:
|
|
|
|
|
|
Obviously, the information delivered by ascertaining the state of the system 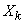 will be maximized when both states
will be maximized when both states 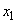 and
and 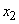 equally likely:
equally likely:
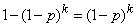 ,
,
from where
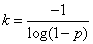 ,
,
Where 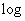 - the binary logarithm sign.
- the binary logarithm sign.
For example, when 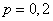 get (rounded to the nearest integer)
get (rounded to the nearest integer)
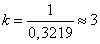 .
.
If information is expressed in binary units, then it can be given a rather visual interpretation, namely: measuring information in binary units, we conditionally characterize it by the number of “yes” or “no” answers, with the help of which you can acquire the same information. Indeed, consider a system with two states:
|
|
|
|
|
|
To find out the state of this system, it is enough to ask one question, for example: is the system in a state of 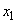 ? The answer “yes” or “no” to this question delivers some information that reaches its maximum value of 1, when both states are a priori equally probable:
? The answer “yes” or “no” to this question delivers some information that reaches its maximum value of 1, when both states are a priori equally probable: 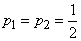 . Thus, the maximum information given by the answer “yes” or “no” is equal to one binary one.
. Thus, the maximum information given by the answer “yes” or “no” is equal to one binary one.
If the information from a message is 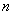 binary units, it is equivalent to the information given
binary units, it is equivalent to the information given 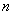 “yes” or “no” answers to the questions posed in such a way that “yes” and “no” are equally likely.
“yes” or “no” answers to the questions posed in such a way that “yes” and “no” are equally likely.
In some of the simplest cases, in order to clarify the content of a message, it is indeed possible to pose several questions so that the answers “yes” and “no” to these questions are equally likely. In such cases, the information received is actually measured by the number of such questions.
If, however, it is not possible to raise questions in this way, it can only be stated that the minimum number of questions needed to clarify the content of a given message is no less than the information contained in the message. For the number of questions to be minimal, it is necessary to formulate them so that the probabilities of the “yes” and “no” answers are as close as possible to 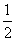 .
.
Example 6. Someone conceived any integer  from one to eight
from one to eight
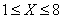 ,
,
and we are invited to guess it by putting the minimum number of questions, each of which is answered "yes" or "no."
Decision. We determine the information contained in the message, what number is intended. A priori, all values  from 1 to 8 are equally likely:
from 1 to 8 are equally likely: 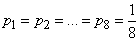 , and the formula (18.5.2) gives
, and the formula (18.5.2) gives
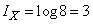 .
.
The minimum number of questions that need to be posed to clarify the conceived number is at least three.
In this case, you can really get by with three questions if you formulate them so that the probabilities of the “yes” and “no” answers are equal.
Let, for example, the number “five” be conceived, we do not know this and ask questions:
Question 1. Number  less than five?
less than five?
Answer. Not. (Conclusion:  - one of the numbers 5, 6, 7, 8.)
- one of the numbers 5, 6, 7, 8.)
Question 2. Number  less than seven?
less than seven?
Answer. Yes. (Conclusion:  - one of the numbers 5, 6.)
- one of the numbers 5, 6.)
Question 3. Number  less than six?
less than six?
Answer. Yes. (Conclusion: number  equal to five.)
equal to five.)
It is easy to make sure that with three such (or similar) questions you can set any conceived number from 1 to 8.
So we learned how to measure information about the system.  contained in both individual reports on its condition, and in the very fact of finding out the state. It was assumed that the observation is carried out directly behind the system itself.
contained in both individual reports on its condition, and in the very fact of finding out the state. It was assumed that the observation is carried out directly behind the system itself.  . In practice, this is often not the case: it may turn out that the system
. In practice, this is often not the case: it may turn out that the system  not directly accessible for observation, and the state of the system itself is not determined
not directly accessible for observation, and the state of the system itself is not determined  and some other system
and some other system 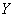 associated with her. For example, instead of directly observing air targets at the control station of air defense weapons, a tablet or a screen displaying the air situation is observed, in which the targets are depicted with conventional icons. Instead of direct observation of the spacecraft, the system of signals transmitted by its equipment is monitored. Instead of text
associated with her. For example, instead of directly observing air targets at the control station of air defense weapons, a tablet or a screen displaying the air situation is observed, in which the targets are depicted with conventional icons. Instead of direct observation of the spacecraft, the system of signals transmitted by its equipment is monitored. Instead of text  The telegram sent by the recipient observes the text.
The telegram sent by the recipient observes the text. 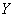 adopted which does not always coincide with
adopted which does not always coincide with  .
.
Differences between the system we are interested in  and directly observable
and directly observable 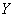 generally can be of two types:
generally can be of two types:
1) Differences due to the fact that some system states  not reflected in the system
not reflected in the system 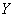 which is “poorer in detail” than the system
which is “poorer in detail” than the system  .
.
2) Differences due to errors: inaccuracies in measuring system parameters  and error when sending messages.
and error when sending messages.
An example of differences of the first type can serve as differences arising from the rounding of numerical data and in general with a rough description of the properties of the system  a display system
a display system 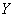 . Examples of differences of the second type can be distortions of signals arising due to noise (noise) in communication channels, due to malfunctions of transmitting equipment, due to distraction of people participating in the transmission of information, etc.
. Examples of differences of the second type can be distortions of signals arising due to noise (noise) in communication channels, due to malfunctions of transmitting equipment, due to distraction of people participating in the transmission of information, etc.
In the case when the system we are interested in  and observable
and observable 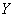 different, the question arises: how much information about the system
different, the question arises: how much information about the system  gives the observation system
gives the observation system 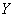 ?
?
It is natural to define this information as a decrease in the entropy of the system.  as a result of obtaining information about the state of the system
as a result of obtaining information about the state of the system 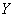 :
:
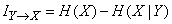 . (18.5.5)
. (18.5.5)
Indeed, before getting information about the system 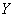 entropy system
entropy system  was
was 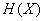 ; after receiving the information "residual" entropy became
; after receiving the information "residual" entropy became 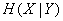 the entropy destroyed by information is information
the entropy destroyed by information is information 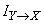 .
.
The value (18.5.5) we will call complete (or average) information about the system  contained in the system
contained in the system 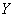 .
.
Prove that
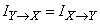 ,
,
that is, each of the two systems contains the same complete information with respect to the other.
For proof, we write the entropy of the system 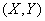 according to the theorem on p. 479, two equivalent formulas:
according to the theorem on p. 479, two equivalent formulas:
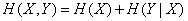 ,
,
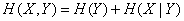 ,
,
from where
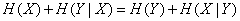 ,
,
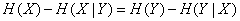 ,
,
or
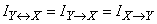 , (18.5.6)
, (18.5.6)
Q.E.D.
We introduce the notation:
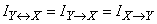 (18.5.7)
(18.5.7)
and will call information 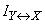 complete mutual information contained in systems
complete mutual information contained in systems  and
and 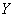 .
.
Let us see what the complete reciprocal information turns to in extreme cases of complete independence and complete dependence of the systems. If a  and
and 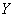 independent then
independent then 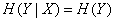 and
and
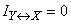 , (18.5.8)
, (18.5.8)
that is, the complete mutual information contained in independent systems is zero. This is quite natural, since it is impossible to obtain information about the system, watching instead of it another, not connected with it.
Consider another extreme case when the system state  completely determines the state of the system
completely determines the state of the system 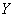 and vice versa (systems are equivalent). Then
and vice versa (systems are equivalent). Then 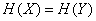 :
:

and
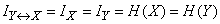 , (18.5.9)
, (18.5.9)
that is, we get the case, which we have already considered above (formula (18.5.2)), when we observe the system that directly interests us  (or equivalently,
(or equivalently, 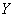 ).
).
Consider the case where between systems  and
and 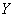 There is a strong dependence, but one-sided: the state of one of the systems completely determines the state of the other, but not vice versa. We will agree to call that system, the state of which is completely determined by the state of another, “subordinate system”. According to the state of the subordinate system, it is generally impossible to unambiguously determine the state of another. For example, if the system
There is a strong dependence, but one-sided: the state of one of the systems completely determines the state of the other, but not vice versa. We will agree to call that system, the state of which is completely determined by the state of another, “subordinate system”. According to the state of the subordinate system, it is generally impossible to unambiguously determine the state of another. For example, if the system  represents the full text of the message, composed of a series of letters, a
represents the full text of the message, composed of a series of letters, a 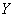 - its abbreviated text, in which all vowels are omitted, then reading in the message
- its abbreviated text, in which all vowels are omitted, then reading in the message 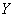 the word "stell", you can not be exactly sure, it means "table", "chair", "became" or "tired."
the word "stell", you can not be exactly sure, it means "table", "chair", "became" or "tired."
Obviously, the entropy of the subordinate system is less than the entropy of the system to which it is subordinate.
We define complete mutual information contained in systems of which one is subordinate.
Let two systems  and
and 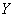 subordinate is
subordinate is  . Then
. Then 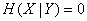 and
and
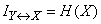 , (18.5.10)
, (18.5.10)
that is, the complete mutual information contained in systems of which one is subordinate is equal to the entropy of the subordinate system.
We derive the expression for information 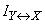 not through conditional entropy, but directly through the entropy of the combined system
not through conditional entropy, but directly through the entropy of the combined system 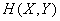 and the entropy of its components
and the entropy of its components 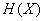 and
and 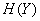 .
.
Using the entropy theorem of the unified system (p. 479), we get:
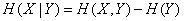 . (05/18/11)
. (05/18/11)
Substituting this expression into formula (18.5.5), we get:
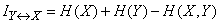 , (18/05/12)
, (18/05/12)
that is, the complete mutual information contained in the two systems is equal to the sum of the entropies of the constituent systems minus the entropy of the combined system.
On the basis of the dependences obtained, it is easy to derive a general expression for complete mutual information in the form of a mathematical expectation. Substituting in (18.5.12) the expressions for entropy:
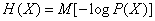 ,
, 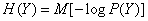 ,
,
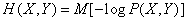 ,
,
will get
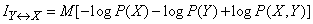
or
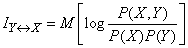 . (18.5.13)
. (18.5.13)
For the direct calculation of complete mutual information, it is convenient to write the formula (18.5.13) in the form
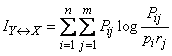 , (18.5.14)
, (18.5.14)
Where
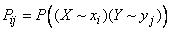 ,
,
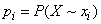 ;
; 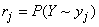 .
.
Example 1. Find complete mutual information contained in systems  and
and 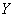 in the conditions of example 1
in the conditions of example 1  18.4.
18.4.
Decision. From example 1  18.4 using table 7 of the application we get:
18.4 using table 7 of the application we get:
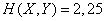 ;
; 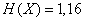 ;
; 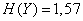 ;
;
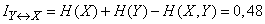 (two units).
(two units).
Example 2. Physical system  can be in one of four states
can be in one of four states 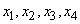 ; corresponding probabilities are given in the table
; corresponding probabilities are given in the table
|
|
|
|
|
| 0.1 | 0.2 | 0.4 | 0.3 |
When monitoring the system  states
states 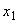 and
and 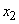 indistinguishable; states
indistinguishable; states  and
and 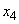 also indistinguishable. System message
also indistinguishable. System message  indicates whether it is in one of the states
indicates whether it is in one of the states 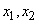 or in one of the states
or in one of the states 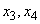 . A message was received indicating in which of the states:
. A message was received indicating in which of the states: 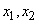 or
or 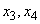 - there is a system
- there is a system  . Identify the information contained in this message.
. Identify the information contained in this message.
Decision. In this example, we are not observing the system itself.  and subordinate system
and subordinate system 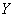 which takes a state
which takes a state 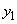 when the system
when the system  turns into one of the states
turns into one of the states 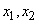 and state
and state 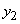 when
when  turns into one of the states
turns into one of the states 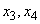 . We have:
. We have:
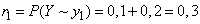 ;
;
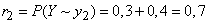 .
.
We find mutual information, that is, the entropy of the subordinate system:
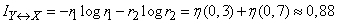 (two units).
(two units).
Entropy and amount of information .
The main feature of random events is the lack of complete confidence in the outcome of the event, which creates the uncertainty of the experiments that implement these events. The degree of uncertainty of random events varies. For example, the experience of tossing a coin. Since the degree of uncertainty of the outcome of an experience is determined by the number of outcomes (sunrise, chess), it is obvious that the function measuring this uncertainty should depend on the number of outcomes. We construct a function, for this we formulate the requirements:
1) if the number of outcomes of the experiment is k = 1, then the degree of uncertainty is f (1) = 0.
2) the more possible outcomes, the greater the degree of uncertainty.
To build a function, consider a complex experience:
α - coin flip
β - toss of the dice.
Favorable outcome will be considered the simultaneous loss of the "coat of arms" and "3". We require that the uncertainty of the first experience be added to the uncertainty of the second experience. f (αβ) = f (α) + f (β) - the logarithm function conditionally satisfies this. Then, if experience has k equal outcomes, then the degree of uncertainty is logak, a = 2, f (k) = log2k. f (2) = log22 = 1 bit - the degree of uncertainty of the experience, with 2 equilibrium outcomes.
lg10 = 1 dit; 1 dit = 3⅓ bits.
Probability: coat of arms - ½, figure - ½. Consider how much uncertainty introduces to each of the outcomes.
½ log2 2 = -½ log2½ = - pilog2pi, when log2 1 = 1. If the outcomes are not equiprobable, then H [α] = -∑ki = 1 pilog2pi (*) . The degree of uncertainty of the experiment α, having k outcomes is determined by the formula (*). H is called the entropy of experience α.
Entropy properties:
1) entropy is always positive, H [α]> 0
2) when pi à0 or pi à1, the entropy tends to 0, H [α] a0.
3) entropy reaches a maximum, if pi = pj, for any i, j all outcomes are equiprobable.
Examples: 1) there are 2 ballot boxes, each with 20 balls. In the first urn 10 white, 5 black, 5 red. In the second urn: 8 white, 8 black, 4 red. From each urn choose a ball. The outcome of each of these experiments should be considered more uncertain.
1) probability: white - ½, black - 1/4, red - 1/4.
2) probability: white - 2/5, black - 2/5, red - 1/5.
H [α1] = −1 log2½ - 1 / 4log21 / 4 - 1 / 4log21 / 4 = ½ + ½ + ½ = 1.5 bits.
H [α2] = -2/5 log22 / 5 - 2 / 5log22 / 5 - 1 / 5log21 / 5 = 1.52 bits.
Answer: the outcome of the second experiment should be considered more uncertain by 0.02 bits.
Entropy is defined as a measure of the uncertainty of the state of some systems. Obviously, as a result of receiving a message, knowledge of the state of the system increases, and the degree of uncertainty of the system decreases. If the message carries full information about the state of the system, then the uncertainty becomes equal to 0. Thus, the magnitude of the information obtained can be estimated by the change in entropy. Hence, the amount of information about the experiment α can be estimated as J [α] = H [α] -Hε [α] (1).
H [α] is the initial entropy, Hε [α] is the residual entropy.
If complete information about the object is obtained, then J [α] = H [α] (2).
In the particular case when pi = pj, for any i, j, then J [α] = -∑ki = 1pilogpi = -k * 1 / k * log21 / k = log2k, i.e. with an equilibrium outcome, J [α] = log2k.
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory