6.1 Corrective properties of redundant codes.

Lecture 6

6.1 Corrective properties of redundant codes.

Consider the essence of noise-resistant coding in the figure already considered in the previous lecture

<! [if! vml]> 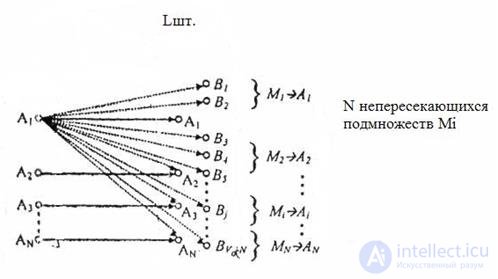<! [endif]>

Fig.6.1

In this figure, Ai (N units) denoted allowed code words, Bj (LN) units. forbidden words, and Mi ( N pieces) are some subsets whose elements are those or other forbidden code words.

It can be seen from the figure that, when transmitting a code combination Ai, it can, under the influence of interference, go into one of the combinations Bj , that is, an error can be detected ( L - N ) from the total number L of code words. This happens every time any of the N allowed code combinations is transmitted . The total number of erroneous combinations that are detected is N ( L - 1 ) and the total number of possible L * N combinations is therefore the proportion of the erroneous combinations that are detected are equal to

µ = 1- (N / L);

A similar technique is used to correct errors. To use the code as a corrective, it is necessary to split the sets Bj of the whole (LN) pcs. forbidden code combinations - on N disjoint subsets of Mi. Each of the subsets Mi is assigned to one of the code words Ai . The method of correcting or correcting errors is that when the received combination Bj belongs to M i , then it is considered that the combination A i is transmitted. With this method of decoding, there is the possibility of correcting errors.

From the figure it can be seen that with any method of breaking the error can be corrected in LN (for Bj) cases and found in N ( L - N ) cases. The ratio of the number of erroneous combinations that are corrected to the number of erroneous combinations is 1 / N.

Finally, we determine that the number of errors that are not corrected is N * (N-1) , while the part of uncorrectable errors in relation to the total number of consequences is equal to ( N -1) / L. Reported results are of a general nature and are correct for all corrective measures.

We talked about corrective properties of redundancy codes.

We now consider simple examples that associate code distance d with corrective code properties.

Obviously, with the code distance d = 1, all code combinations are allowed.

For example, when n = 3, the allowed combinations form the following set:

000,001,010,011, 100, 101, 110, 111 with a code distance of d = 1 .

Any single error transforms this combination into another allowed combination. This is a case of a non-redundant code that does not have a corrective power.

If d = 2 , then none of the allowed code combinations for a single error does not go into another allowed combination. For example, a subset of the allowed code combinations can be formed by the parity principle in it the number of units. For example, for n = 3 , d = 2 :

011 , 101 , 110- allowed combinations;

010 , 100 , 111 - forbidden combinations.

For any single error, the allowed combination turns into a forbidden one. The code detects single errors, as well as other errors of odd multiplicity.

In the general case, if it is necessary to detect errors of multiplicity up to g inclusive, the minimum Hamming distance between the allowed code combinations must be at least one greater than r , that is, d > r + 1 .

Indeed, in this case, an error, the multiplicity of which does not exceed r , is not able to translate one allowed code combination into another.

To correct a single error of a code combination, it is necessary to map a subset of the forbidden code combinations to the set of source code combinations.

To prevent these subsets from intersecting, the Hamming distance between the allowed code combinations must be at least three. When n = 3, the allowed code combinations can be, for example, 000 and 111 with d = 3 . Then the allowed combination 000 must be attributed to a subset of the forbidden code combinations 001 , 010 , 100 , resulting from a binary error in the combination 000 .

In a similarly permitted combination 111, it is necessary to assign a subset of the forbidden code combinations: 110 , 011 , 101 , resulting from the occurrence of a single error in the 111 combination:

The allowed combinations 000 correspond to prohibited combinations 001 010 100 .

If any code word from this set is accepted, then by the maximum likelihood principle it can be assumed that code word 000 was transmitted.

The allowed combinations 111 correspond to prohibited combinations 011 101 110 .

If any code word from this set is accepted, then code word 111 was transmitted according to the maximum likelihood principle.

Thus for code 000 and 111 with d = 3 one error can be corrected.

In the general case, in order to be able to correct all errors of multiplicity up to s inclusive, each of the errors should lead to a forbidden combination relating to a subset of the original allowed code combination.

The error will not only be detected, but also corrected if the distorted combination remains closer to the original than to any other allowed combination, that is, it should be:

d> = 2S + 1;

Consider the geometric interpretation of the code distance d and its relationship with the number of errors detected and corrected.

To identify arbitrary errors that change in code words, not more than r characters, it is necessary and sufficient that no r- fold errors translate one code word of the code into another, see figure 6.2

<! [if! vml]> 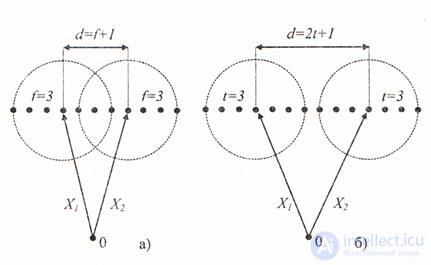<! [endif]>

Fig.6.2

This condition will be satisfied if the code combinations are chosen so that among them there are none that are at a distance less than r + 1 . If such a code is used to encode a message, then the received code word Y , which is not on the list of allowed words, is a sign of error detection. The 4 combinations considered earlier, 000 , 011 , 101 , 110 , represent the code with the detection of a single error, because for them the code distance is d = 2 . In order for the code to correct all errors, the multiplicity of which does not exceed s , the vectors of each pair Xi, Xj must be located one from another at a distance not less than 2s + 1 .

In the general case, to detect errors of multiplicity r , simultaneous correction of errors of multiplicity s , the condition

d> = r + s + 1 .

The code distance only partially characterizes the quality of the code, because, in addition to errors that are fully corrected or detected, errors of greater multiplicity are often detected or corrected.

Consider the concept of quality correction code in more detail.

One of the main characteristics of the correction code is code redundancy, which indicates the degree of extension of the code combination to achieve a specific correction ability.

If for every n characters of the output sequence of a channel coder there are k information and r check, then the relative redundancy of the code can be expressed as:

ρ = (nk) / n = r / n = 0… 1;

Codes that provide the specified correction ability with the lowest possible redundancy are called optimal.

In connection with finding optimal codes, let us estimate, for example, the possible maximum number Q of allowed or informational combinations of an n- digit binary code that has the ability to correct mutually independent multiplicity errors up to s inclusive. This is equivalent to finding the number of combinations, the code distance between which is not less than d = 2s + l.

The total number of different fixable errors for each allowed combination is

_{<! [if! vml]> 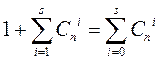<! [endif]>}

where С _n ⁱ is the number of errors of multiplicity i <s.

Each of these errors should lead to a forbidden combination that belongs to a subset Mi for a given allowed combination. Together with this allowed combination, the subset includes just so many combinations.

_{<! [if! vml]> 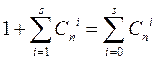<! [endif]>}

Unambiguous decoding is possible only in the case when the specified subsets do not overlap. Since the total number of different combinations of an n- digit binary code is 2 ⁿ , the number of allowed combinations cannot exceed

_{<! [if! vml]> 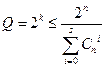<! [endif]>}

This upper bound was found by Hamming. For some specific values ​​of code distance d , the corresponding Q will be indicated in the table:

Table 6.1

<! [if! vml]> 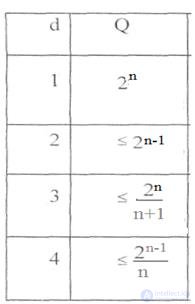<! [endif]>

Codes for which equality is achieved in the above ratio are also called densely packed .

However, it is not always advisable to strive to use codes that are close to optimal. It is necessary to consider another, no less important indicator of the quality of the correction code - the complexity of the technical implementation of the encoding and decoding processes . There must be a trade-off between the corrective properties of the code and the complexity of the technical implementation.

If information is to be transmitted but slowly operating and expensive communication lines, and the encoding and decoding devices are supposed to be performed on highly reliable and fast-acting elements, then the complexity of these devices does not play a significant role. In this case, the decisive factor is an increase in the efficiency of using the communication line; therefore, it is desirable to use correction codes with minimal redundancy.

If the correction code must be applied in a system made on elements whose reliability and speed are equal or close to the reliability and speed of elements of the coding and decoding equipment. This is possible, for example, to increase the reliability of reproduction of information from a computer storage device. Then the criterion of the quality of the correction code is the reliability of the system as a whole, that is, taking into account possible distortions and failures in the encoding and decoding devices. In this case, codes with more redundancy, but simple in technical implementation, are often more appropriate.

6.2 Classification of correction codes.

The general classification, convenient from the point of view of the following study of the most important classes of codes, is presented in Figure 6.3.

<! [if! vml]> 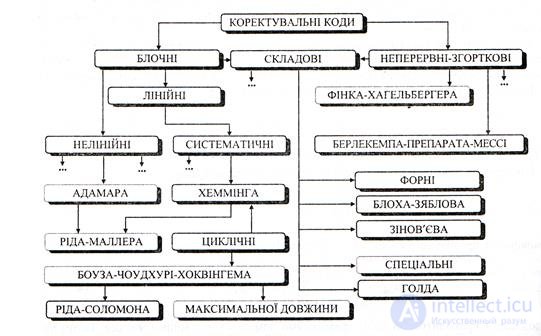<! [endif]>

Fig.6.3

Correction codes can be divided into two large classes: block and continuous.

Block codes consist of separate combinations (blocks) that are encoded and decoded independently.

Continuous or convolutional codes represent a continuous sequence of code symbols, its division into separate code combinations is not carried out .. The name of these codes comes from the fact that the original sequence of a continuous code represents a convolution of the input information sequence with the impulse response of the code. Composite (combined, derivative, product codes, special, etc.) correction codes are built on the basis of block or block and continuous codes. These codes are also called cascade codes.

A block code is called linear if all its code words form a linear vector space. Thus, a new allowed code combination can be obtained as a linear combination of other allowed code words, otherwise the code is called non-linear. A systematic code is a code in which code words consist of k information and r check characters, while the positions of the information and check characters are the same for all code words of the code. Such the formation of code combinations greatly simplifies the technical implementation of the device encoding and decoding. Therefore, systematic codes are among the most common.

Under the class of linear (systematic) codes are Hamming codes and cyclic codes, for example, Bose-Choudhury-Hokvingem codes (BCH codes). A rare case of BCH codes are maximum length codes (M-sequences). According to the established tradition, a number of subclasses of correction codes mark the names of those scientists who first proposed and investigated this or that type of encoding.

Features of construction and characteristics of many codes highlighted in the figure is a subject of further consideration.

6.3 Test questions.

1. What makes error detection different from fixing it?

2. Connection of code distance with the number of detected errors.

3. Connection of code distance with the number of corrected errors.

4. What is the meaning of Hamming estimate for the amount of code with a given code distance?