14.1 Coding of repetition lengths.

14 1 Coding length repetitions.

Encoding of lengths of sections (or repetitions) can be quite effective in compressing binary data, for example, black and white facsimile images, black and white images containing a multitude of straight lines and homogeneous sections, schemes, etc. Encoding of repetition lengths is one of the elements of the well-known JPEG image compression algorithm.

The idea of ​​data compression based on the coding of repetition lengths is that instead of coding the actual data, the numbers corresponding to the lengths of the sections in which the data retains the same value are encoded.

Suppose that you need to encode a black and white (two-color) image size of 8 x 8 elements, shown in Figure. 14.1

Fig. 14.1

We will scan this image in rows (two colors in the image will correspond to 0 and 1), resulting in a double vector data

X = (0111000011110000000100000001000000010000000111100011110111101111)

64 bits long (source code is 1 bit per image element).

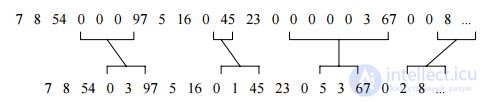
In the vector X , we select the sections where the data remain constant, and determine their lengths. The resulting sequence of lengths of plots-positive integers corresponding to the initial data vector X, will have the form r = (1, 3, 4, 4, 7, 1, 7, 1, 7, 1, 7, 4, 3, 4, 1, 4 , 14).

Now this sequence, in which a certain repeatability is noticeable (units and quadruples are much larger than other characters), can be encoded with some statistical code, for example, a Shannon-Fano code without memory, having a coding table (Table 15.1)

Table 14.1

In order to indicate that the encoded sequence starts from zero, add the prefix character 0 at the beginning of the code word. As a result, we get the code word B (r) = (0100011010110101101011001110100100) 34 bits long, that is, the resulting code rate R will be 34/64, or just over 0.5 bits per image element. When compressing images of a larger size and containing many repetitive elements, the compression efficiency can be significantly higher.

There is another method of using repetition length coding, when in digital data there are areas with a large number of zero values. Whenever a “ zero ” occurs in the data stream, it is encoded with two numbers. The first is 0, which is the flag for the start of encoding of the stream of zeros, and the second is the number of zeros in the next group. If the average number of zeros in a group is more than two, compression will take place. On the other hand, a large number of individual zeros can even lead to an increase in the size of the file being encoded:

Another simple and widely used lossless encoding method for image and audio compression is the differential encoding method.

14 2 Differential coding.

The operation of the differential encoder is based on the fact that for many types of data the difference between adjacent samples is relatively small, even if the data itself has large values. For example, one cannot expect a big difference between neighboring pixels of a digital image, for example, for landscape, household or genre photography. Another thing, if we photograph a bar code or a herd of zebras.

The following simple example shows what advantage differential coding can give (coding the difference between adjacent samples) in comparison with simple coding without memory (coding samples independently of each other).

We scan an 8-bit (256-level) digital image, and at the same time, let ten consecutive pixels have levels:

144, 147, 150, 146, 141, 142, 138, 143, 145, 142.

If we encode these levels pixel by pixel with some code without memory, using 8 bits per image pixel, we get a code word containing 80 bits.

Suppose now that before subjecting the image samples to coding, we calculate the differences between neighboring pixels. This procedure will give us the following sequence:

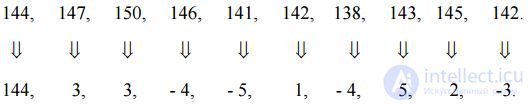
The original sequence can be easily reconstructed from a difference by simple summation (discrete integration):

To encode the first number from the resulting sequence of sample differences, as before, you need 8 bits, all other numbers can be encoded with 4-bit words (one sign bit and 3 bits for coding the modulus of a number).

Thus, as a result of coding, we will obtain a code word of length 8 + 9 * 4 = 44 bits, or almost twice as short as with individual coding of samples.

The method of differential encoding is very widely used in cases where the nature of the data is such that their neighboring values ​​differ slightly from each other, while the values ​​themselves can be arbitrarily large.

This applies to audio signals, especially to speech, images whose neighboring pixels have almost the same brightness and color, etc. At the same time, this method is completely unsuitable for encoding texts, drawings, or some kind of digital data with independent neighboring values.

14 3 Test questions .

1. For what situations is the repetition length coding method preferred?

2. For what situations is the differential encoding method preferred?