10.1 Informational characteristics of continuous message sources.

Topic 7. Information characteristics of the sources of continuous messages. Sources with maximum entropy. Maximum bandwidth communication channel with interference.

Lecture 10 .

10.1 Informational characteristics of continuous message sources.

 

Consider the issues related to information and relevant characteristics in the transmission of continuous messages (continuous functions of time), and find out what features are there in this case.

The main informational characteristics of sources and channels of continuous messages are defined in the same way as for sources and channels of discrete messages. The formula for the entropy of the source of continuous messages is obtained by passing to the limit from the formula for the entropy of a discrete source.

_{<! [if! vml]> 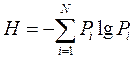<! [endif]>}

Let the one-dimensional probability distribution of the random stationary process X (t) be W (x), then the probability that X (t) will be in the interval [x _i , x _i + Δx] is equal to p _i = W (x _i ) * ∆x . If the signal is quantized into L levels, then the entropy of the source of continuous messages to one sample

<! [if! supportTextWrap]>
<! [endif]>

As a result of the passage to the limit as ∆x → 0, we obtain the value

 

<! [if! supportTextWrap]>
<! [endif]>

 

which is called the differential entropy of the source of continuous messages. Differential - because the differential distribution law W (x) participates in it .

The information transfer rate, bandwidth and other basic information characteristics of the source of the message and the transmission channel are determined by the difference of the differential entropies.

Indeed, we find, for example, mutual information between two continuous random processes X (t) and Y (t) at an arbitrary time t.

Considering that

<! [if! supportTextWrap]>
<! [endif]>

 

where W ₂ (x _i , y _j ) is the compatible probability density X and Y ;

p (x _i ) = W ₁ (x _i ) * ∆x; p (y _j ) = W ₁ (y _j ) * Δy ,

we obtain an expression for mutual information between X and Y.

 

<! [if! supportTextWrap]>
<! [endif]>

 

Applying for this expression a contraction, and then a passage to the limit, we get

 

<! [if! supportTextWrap]>
<! [endif]>

 

 

where h (X) and h (Y) are the differential entropies for counting random processes X (t) and Y (t), and

<! [if! supportTextWrap]>
<! [endif]>

- - conditional differential entropy of reference X (t) with a known reference Y (t).

AND

<! [if! supportTextWrap]>
<! [endif]>

- conditional differential entropy of the reference Y (t) with a known reference X (t).

Thus, mutual information is the final value. Note that differential entropy is not an absolute measure of its own information; it characterizes only that part of the entropy of a continuous message, which is determined by the form of the law of probability distribution W (x). Let us find the value of differential entropy for specific laws of probability distributions.

 

10.2 Entropy of the uniform distribution law.

 

Entropy of the uniform distribution law . For a uniform distribution, W (x) = 1 / (ba). Using the formula for differential entropy, we obtain

<! [if! supportTextWrap]>
<! [endif]>

 

As the interval (ba) increases, the h (X) value also increases.

 

10 3 Entropy of the Gaussian distribution law .

Entropy of the Gaussian distribution law. Let us find the probability density of a stationary random process X (t), with a limited average power, which provides the maximum h (X). in other words, it is necessary to find the maximum of the function in the following statement: the objective functional is given:

<! [if! vml]>

<! [endif]>

 

<! [if! vml]>

<! [endif]>
and limitations

 

Find a W (x) that delivers the maximum entropy h (X).

The solution of this problem is known, and leads to the fact that the desired probability density satisfying the maximization conditions is a Gaussian function

<! [if! vml]>

<! [endif]>

and maximum entropy

<! [if! supportTextWrap]>
<! [endif]>

 

Consequently, among all sources of a random signal with a limited and equal average power (dispersion), the source with the Gaussian distribution of the signal has the greatest entropy.

In practice, we always deal with signals (messages and interference) of finite length and finite energy. Moreover, if the duration of the signal is T _s , and its spectral width is ∆f , then without loss of information such a continuous message can be represented by N = T _s * 2∆f by independent samples. Thus, for a Gaussian distribution, the entropy of a continuous message segment of duration T _s will be equal to

_{<! [if! vml]> 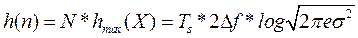<! [endif]>}

 

10 3 Test questions .

1. Explain the relativity of differential entropy.

2. What is the distribution law of the highest entropy at the same process dispersion?