Lecture
In the previous  we reviewed the complete (or average) system information
we reviewed the complete (or average) system information 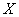 contained in the message about the state of the system
contained in the message about the state of the system 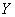 . In some cases it is of interest to evaluate private information about the system.
. In some cases it is of interest to evaluate private information about the system. 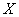 contained in a separate message indicating that the system
contained in a separate message indicating that the system 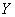 is in a specific state
is in a specific state 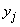 . Denote this private information
. Denote this private information 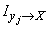 . Note that complete (or, otherwise, average) information
. Note that complete (or, otherwise, average) information 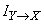 should be the expectation of private information for all possible states about which the message can be transmitted:
should be the expectation of private information for all possible states about which the message can be transmitted:
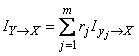 . (18.6.1)
. (18.6.1)
Give the formula (18.5.14), which is calculated 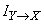 (she
(she 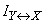 ), a view like that of formula (18.6.1):
), a view like that of formula (18.6.1):
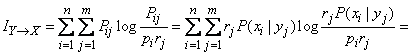
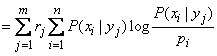 , (18.6.2)
, (18.6.2)
whence, comparing with formula (18.6.1), we obtain the expression of private information:
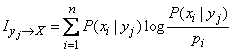 . (18.6.3)
. (18.6.3)
Expression (18.6.3) and take for the definition of private information. Let's analyze the structure of this expression. It is nothing more than averaged over all states. 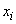 value of magnitude
value of magnitude
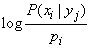 . (18.6.4)
. (18.6.4)
Averaging occurs taking into account different probabilities of values 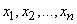 . Since the system
. Since the system 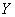 already accepted the state
already accepted the state 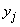 then when averaging the values (18.6.4) do not multiply by the probability
then when averaging the values (18.6.4) do not multiply by the probability 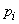 states
states 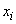 , and on conditional probabilities
, and on conditional probabilities 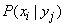 .
.
Thus, the expression for private information can be written in the form of conditional expectation:
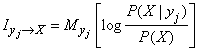 . (18.6.5)
. (18.6.5)
We prove that private information 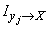 , as well as complete, can not be negative. Indeed, we denote:
, as well as complete, can not be negative. Indeed, we denote:
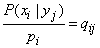 (18.6.6)
(18.6.6)
and consider the expression
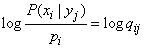 .
.
It is easy to see (see Fig. 18.6.1) that for any 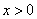
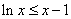 . (18.6.7)
. (18.6.7)
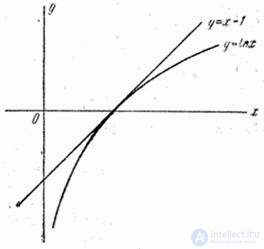
Fig. 18.6.1.
Putting in (18.6.7) 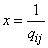 , we get:
, we get:
 ;
; 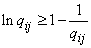 ,
,
from where
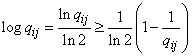 . (18.6.8)
. (18.6.8)
Based on (18.6.3) and (18.6.6) we have:
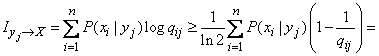
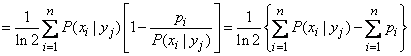 .
.
But
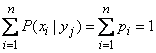 ,
,
and the expression in the brace is zero; Consequently 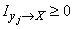 .
.
Thus, we have proved that private information about the system 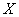 enclosed in a message about any condition
enclosed in a message about any condition 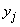 systems
systems 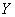 can not be negative. It follows that non-negative and complete mutual information
can not be negative. It follows that non-negative and complete mutual information 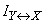 (as the mathematical expectation of a non-negative, random variable):
(as the mathematical expectation of a non-negative, random variable):
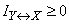 . (18.6.9)
. (18.6.9)
From the formula (18.5.6) for information: 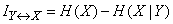 follows that
follows that
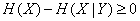 (18.6.10)
(18.6.10)
or
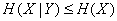 ,
,
that is, the total conditional entropy of the system does not exceed its unconditional entropy.
Thus, the position taken by us on faith in  18.3.
18.3.
For the direct calculation of private information, it is convenient to slightly convert the formula (18.6.3) by entering into it instead of conditional probabilities 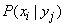 unconditional. Really,
unconditional. Really,
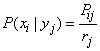 ,
,
and the formula (18.6.3) takes the form
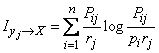 . (18.6.11)
. (18.6.11)
Example 1. System 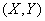 characterized by a probability table
characterized by a probability table 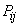 :
:
|
|
|
|
| 0.1 | 0.2 | 0.3 |
| 0.3 | 0.4 | 0.7 |
| 0.4 | 0.6 |
Find private system information 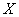 enclosed in a message
enclosed in a message 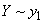 .
.
Decision. By the formula (18.6.11) we have:
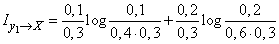 .
.
According to table 6 of the application we find
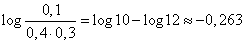 ,
,
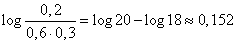 ,
,
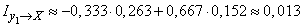 (two units).
(two units).
We defined private system information. 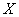 contained in a specific event
contained in a specific event 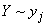 i.e. in the message “system
i.e. in the message “system 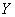 is able to
is able to 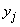 ". A natural question arises: is it possible to go even further and determine private information about the event?
". A natural question arises: is it possible to go even further and determine private information about the event? 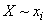 contained in the event
contained in the event 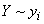 ? It turns out that this can be done, only the information “from an event to an event” obtained in this way will have somewhat unexpected properties: it can be both positive and negative.
? It turns out that this can be done, only the information “from an event to an event” obtained in this way will have somewhat unexpected properties: it can be both positive and negative.
Based on the structure of formula (18.6.3), it is natural to determine the information “from event to event” as follows:
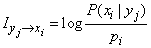 , (18.6.12)
, (18.6.12)
that is, private information about an event, obtained as a result of reporting another event, is equal to the logarithm of the ratio of the probability of the first event after the message to its probability before the message (a priori).
From the formula (18.6.12) it is clear that if the probability of an event 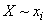 as a result of the message
as a result of the message 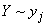 increases, i.e.
increases, i.e.
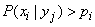 ,
,
that information 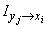 is positive; otherwise, it is negative. In particular, when the occurrence of an event
is positive; otherwise, it is negative. In particular, when the occurrence of an event 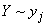 completely excludes the possibility of an event
completely excludes the possibility of an event 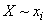 (i.e., when these events are incompatible),
(i.e., when these events are incompatible),
Information 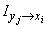 can be written as:
can be written as:
 , (18.6.13)
, (18.6.13)
which implies that it is symmetric with respect to 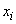 and
and 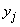 and
and
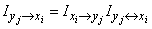 . (18.6.14)
. (18.6.14)
Thus, we have introduced three types of information:
1) complete system information 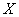 contained in the system
contained in the system 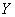 :
:
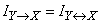 ;
;
2) private information about the system 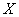 contained in the event (message)
contained in the event (message) 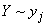 :
:
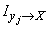
3) private information about the event 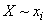 contained in the event (message)
contained in the event (message) 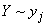 :
:
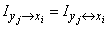 .
.
The first two types of information are non-negative; the latter can be both positive and negative.
Example 2. In the urn 3 white and 4 black balls. 4 balls were taken out of the urn, three of them turned out to be black, and one - white. Determine the information enclosed in the observed event.  in relation to the event
in relation to the event 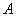 - the next ball drawn from the urn will be black.
- the next ball drawn from the urn will be black.
Decision.
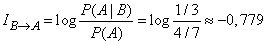 (two units).
(two units).
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory