Lecture
Lecture 3 .
3 1 Redundancy of information , the reasons for its occurrence .
To find the maximum throughput of the communication system, you must be able to determine the maximum amount of information that can be transmitted using the symbols of this alphabet per unit of time. It is known that the maximum amount of information per message symbol H = logN can be obtained only in the case of equiprobable and independent characters. Real sources of messages rarely fully satisfy this condition, so the information load on each of their characters is usually less than what they could carry.
As a rule, the primary source symbols, when transmitted to a communication channel, are encoded to make them look necessary for transmission to a channel, for example, they are encoded into a binary code. In this case, one primary symbol corresponds to the code word of the encoder of the primary source.
Since the information load on each symbol of the primary source is usually less than that which they could transfer, the symbols are underloaded and the message itself has information redundancy.
The concept of redundancy in information theory and coding is introduced to quantitatively describe the information reserve of the code from which the message is composed. The very formulation of such a task became possible precisely because the information is a measurable quantity, whatever the particular type of the message under consideration.
Statistical redundancy is due to the unequal distribution of the symbols of the primary alphabet and their interdependence.
For example, for an English alphabet consisting of 26 letters, the maximum value of entropy
H max = log 2 m = log 2 26 = 4.7 bits
When taking into account the frequency of occurrence of letters in texts, the transmitted information can be significantly compressed, reduced.
The ratio μ = H / H max is called the compression coefficient, or relative entropy, and the value
<! [if! vml]>  <! [endif]>
<! [endif]>
redundancy.
From this expression it is obvious that redundancy is less for those messages that have more entropy of the primary alphabet.
Entropy can be defined as the information load on the message symbol. Redundancy determines the underload of characters. If H = H max , then according to the expression of underload does not exist and D = 0.
In other cases, the same number of code words can be given more characters. For example, by the code word of three binary bits we can transmit 5 and 8 characters.
In fact, to transmit the primary symbol in binary code, it is sufficient to have the length of the code combination when encoding the primary symbols.
<! [if! vml]> 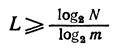 <! [endif]>
<! [endif]>
where N is the total number of transmitted characters, m is the number of characters of the secondary alphabets. For N = 5
<! [if! vml]> 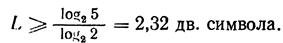 <! [endif]>
<! [endif]>
However, this figure should be rounded to the nearest whole number, since the code length cannot be expressed as a fractional number. Rounding up.
In general, rounding redundancy
<! [if! vml]> 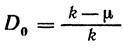 <! [endif]>
<! [endif]>
<! [if! vml]> 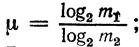 <! [endif]>
<! [endif]>
k - rounded to the nearest integer value of μ .
For our example
<! [if! vml]> 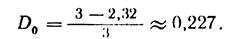 <! [endif]>
<! [endif]>
The digit 0,227 characterizes the degree of code underload.
Consider what can be done to reduce the redundancy of the primary alphabet (source of characters). Consider a message source, issuing the symbols A with a probability of occurrence p (A) = 0.9 and B with p (B) = 0.1
In this case, the entropy of the source is H = 0.47 bps, H max = log2 = 1bit / s.
Redundancy D = 1- (0.47 / 1) = 0.53 .
How to reduce it?
3 2 Ways to reduce redundancy .
We distinguish in the messages of this source two-place blocks of the type AA, AB, BA, BB. Since the symbols A and B are independent, the corresponding probabilities of their appearance are p (AA) = 0.81, p (AB) = 0.09 , p (BA) = 0.09, p (BB) = 0.01 .
In this case, N = 4 ,
H = ∑p i * log (p i ) = 1.14bit / sim,
H max = 2bit / s.
And redundancy
D = 1- (1.14 / 2) = 0.43.
The transition to the block (two-character) encoding of messages of the primary source reduced its redundancy. It can be shown that with a sufficiently large block length, the source redundancy will be sufficiently small.
The redundancy inherent in the nature of the primary source cannot be completely eliminated. However, the redundancy due to the uneven appearance of characters automatically decreases as the length of the code block increases.
This method of reducing the source by encoding messages in blocks is the basis for determining potential coding characteristics for communication channels without interference.
Conclusions: 1. The redundancy of messages composed of equiprobable characters is less than the redundancy of messages composed of not equiprobable characters.
2. Information statistical redundancy of the primary source of messages is a natural phenomenon and such redundancy is incorporated in the statistical characteristics of the primary alphabet.
3. Reducing the redundancy of the message, you can increase the speed of its transmission over the communication channel.
For further discussion, we need the notion of message source performance.
What is the performance of the source. Let the source generate 1 symbol in time τ = 1 µs . Then, if the entropy of the source is for example 2bit / character, then its performance
System. = N / τ = 2Mbit / s .
3 3 Shannon 's theorem for a channel without interference .
The information transmission system, in which the equipment does not introduce any distortions, and the communication channel - attenuation and interference, is called an information system without noise. In such a system, no matter how the signals are encoded, there will be no loss of information. But this does not mean that in such a system all technical problems of information transfer are automatically solved. In order to unambiguously decode received messages, as well as to transfer large amounts of information with less time and material costs, codes must, in particular, satisfy the following requirements:
1. Different characters of the primary alphabet from which messages are composed must have different code combinations.
2. The code must be constructed so that the beginning and end of the code words can be clearly separated.
3. The code should be as short as possible. The smaller the number of elementary code symbols required to transmit a given message, the closer the information transfer rate is to the speed that can theoretically be achieved on a given communication channel.
The first requirement is obvious, since with the same code words for different letters of the alphabets it will not be possible to decode them unambiguously.
The second requirement can be satisfied as follows:
- introducing into the code an additional separator character - a pause, which significantly lengthens the codes, and consequently, the time of message transmission;
- by creating a code in which the end of one code combination cannot be the beginning of another;
- or by creating a code in which all letters are transmitted by combinations of equal length, i.e., uniform code.
It should be noted that uniform codes have known advantages; The length of each letter can be determined by simple counting of elementary symbols, which makes it possible to automate the decoding process and construct simple decoding devices. However, uniform codes have one major drawback: all the code words of the alphabets represented by them have an equal length, regardless of the probability of the appearance of individual characters of the encoded alphabet. Such a code can be optimal only for the case of equiprobable and mutually independent message symbols, which is quite common in telemechanics and never in the transmission of text messages.
In order to find conditions that satisfy the third, basic requirement for codes, it is necessary to find out within what limits the minimum average length of a code word for a given alphabet is located, and also to find conditions under which this length can be reduced.
According to N = m n, in order to transmit N non-repeating messages using m characters of the secondary alphabet, they must be combined into n pieces in a code word. In the case of an equiprobable primary source of N characters, its entropy
H = logN .
Obviously, with this, the length of the code word of the source coder
n = logN / log (m).
Our task is to build a code for a given source of N characters with an average word length close to this value.
For a primary source of messages with an unequal distribution of characters at the output, the possible minimum of the average codeword length
L = H / log (m)
Since in practice you have to transfer messages composed of alphabets with some real entropy, and the developer of the communication system does not depend on increasing or decreasing it directly in the primary alphabet, it is desirable to encode the symbols of the primary alphabet in this way to use the information reserve embedded in the primary alphabet.
This idea was implemented in codes in which the redundancy contained in the primary alphabet is completely or almost completely eliminated by the rational construction of code words in the secondary alphabet.
In this sense, the extremely short are the so-called optimal codes - codes with zero (or close to zero) redundancy. A classic example of code with zero redundancy can be the Shannon-Fano code, the construction of which we will consider in the following lectures.
Thus the value
L = H / log (m)
can serve as a measure of the length of the code word. For the case when N is an integer power of 2,
N = 2 k ,
k is an integer and k is the minimum length of the code word L for encoding the characters of the primary source in a binary alphabet.
For binary alphabets (m = 2)
<! [if! vml]> 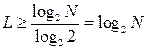 <! [endif]>
<! [endif]>
For m- valued equally probable alphabet, the length of the code word
<! [if! vml]> 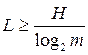 <! [endif]> (BUT)
<! [endif]> (BUT)
Summarizing, we can say that in the general case the average minimum length of the code word L for a primary source of N characters composed of an alphabet with m characters
<! [if! vml]> 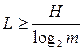 <! [endif]>
<! [endif]>
On the other hand, it can be shown that
<! [if! vml]> 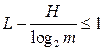 <! [endif]>
<! [endif]>
or
<! [if! vml]> 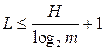 <! [endif]> (AT)
<! [endif]> (AT)
The proof (see, for example, the Tsymbala textbook, ch.14.1413, 114) is based on an obviously understandable relation
[X] -X <1,
where [X] is the integer part of X , that is, the difference between the rounding of the number X to the integer in a large direction and the number X itself is less than 1.
Expressions (A) and (B) are respectively the upper and lower bounds of the minimum necessary average length of the code word. Using these expressions, we get
<! [if! vml]> 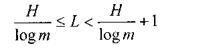 <! [endif]> (C).
<! [endif]> (C).
Let us now consider the conditions under which the difference between the upper and lower limits will decrease, that is, the conditions under which the average minimum length of a codeword will approach the value of H / log (m).
To do this, we first find out the nature of redundancy, which is expressed by the inequality
<! [if! vml]> 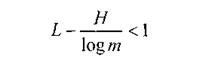 <! [endif]>
<! [endif]>
Suppose that equiprobable symbols of some primary alphabet are transmitted using the uniform binary code m = 2 . For the transmission of eight letters of the alphabet the minimum length of the code word
<! [if! vml]> 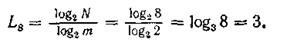 <! [endif]>
<! [endif]>
To transfer five letters
L 2 = log 2 5 = 2.322
that is, the minimum length cannot be transmitted by less than three characters. In this case, the compression ratio
µ = 2.322 / 3 = 0.774
and redundancy
D = 1-µ = 1-0.774 = 0.226
The number 0,226 characterizes the degree of underload of the code. Expression
<! [if! vml]> 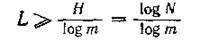 <! [endif]>
<! [endif]>
valid for codes with equiprobable and mutually independent characters.
Let us now consider the case of block-coding (see the example from the first part of the lecture, where each of the blocks consists of M independent letters a 1 , a 2 , ..., a m ).
The expression for the entropy of the message of all the letters of the block, according to the rule of addition of entropy,
<! [if! vml]> 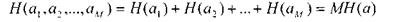 <! [endif]>
<! [endif]>
By analogy with formula (C), we write the expression for the average length of such a code block
<! [if! vml]> 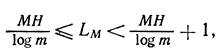 <! [endif]>
<! [endif]>
where L M - the average number of characters in the block.
For such block coding, obviously, the ratio
L M = L * M ,
then
L = Lm / M.
It is easy to see that now L can be obtained by dividing all parts of inequality (C) by M. Then the general expression for the average number of elementary symbols per code per symbol of the primary source of messages
<! [if! vml]> 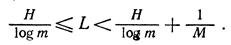 <! [endif]> (D)
<! [endif]> (D)
It is clear from this that when M → ∞, the average number of elementary symbols of a code word spent on the transmission of a single letter is infinitely close to
<! [if! vml]> 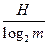 <! [endif]>
<! [endif]>
Expression (D) is the main expression of the fundamental Shannon coding theorem in the absence of noise. The theorem itself can be formulated as follows:
When encoding a set of signals with entropy H in the alphabet, consisting of m characters, in the absence of noise, the average codeword length cannot be less than
<! [if! vml]> 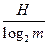 <! [endif]> ,
<! [endif]> ,
exact achievement of the specified border is impossible; but when coding with sufficiently long blocks, this boundary can be arbitrarily approached.
For binary codes, the basic coding theorem can be formulated as follows: when encoding messages in a binary alphabet, with an increase in the number of code words, the average number of binary digits per symbol of the original alphabet approaches the entropy of the message source.
If the encoded alphabet is equiprobable and N = 2 i (where i is an integer), then the average number of binary characters per letter is exactly equal to the entropy of the message source.
Findings:
1. The longer the primary codeword, the more accurate the value
<! [if! vml]> 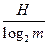 <! [endif]>
<! [endif]>
characterizes the average length of the code word.
2. The more primary symbols in a block, the smaller the difference between the upper and lower bounds, which determine the average number of elementary code symbols per letter of the message.
3. From whatever number of letters the alphabet consists, it is advisable to encode messages not by letter, but block by block.
4. The entropy of the primary alphabet can characterize the possible limit for the reduction of a code word in the secondary alphabet.
3 4 Test questions .
1. What are the reasons for the redundancy of sources of information.
2. What are the basic requirements for codes that reduce the redundancy of the primary source of messages.
3. Formulate the main practical conclusion from the theorem of Shannon for coding in the channel without interference.
Comments
To leave a comment
Information and Coding Theory
Terms: Information and Coding Theory