11.1 Bandwidth of a communication channel with interference for continuous messages

Lecture 11 .

11 1 Bandwidth interference channel for continuous communications

Consider a communication channel with additive Gaussian noise n (t), to the input of which information is received in the form of a continuous signal S (t). The output of such a channel is a random process y (t), each implementation of which can be represented as

y (t) = S (t) + n (t).

The speed of transmission of continuous signals (messages) we define as the difference between the corresponding performance of the channel output and noise in the channel:

R = V * [h (y) -h (n)]

where V = 1 / T _s is the message transmission rate in the channel, which is determined by the transmission time of the signal with duration T _s , and h (y) and h (n) are the differential entropy of the channel output and the noise in the channel, respectively.

Let the effective channel bandwidth, which is selected in accordance with the maximum width of the signal spectrum F _max , be ∆f and the signal transmission time be T _{s .} In this case, the noise performance

R _n (n) = V * h (n), and

_{<! [if! vml]> 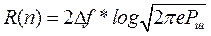<! [endif]>}

where Rsh is the noise power in the ∆f band

The bandwidth of the communication channel is by definition equal to

_{<! [if! vml]> 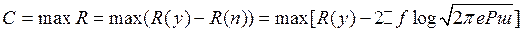<! [endif]>} (*)

where the maximum is found according to all laws of the distribution W (y) - probability density of the process

y (t) = S (t) + n (t)

at the output of the communication channel (at the input of the receiver).

Find the bandwidth of the communication channel under the condition that the average signal power is limited and the noise in the channel is white normal noise.

As before, we will assume that all information losses occur only due to noise. In this case, the maximization of the bandwidth described above reduces to the formation of the signal S (t), so that the process at the output of the communication channel y (t) = S (t) + n (t) has a normal distribution, since such a signal has maximum entropy. This is an extremely important question to consider in more detail.

It is well known from statistics that the process y (t) = S (t) + n (t) has a normal distribution, provided that the noise n (t) is normally distributed, in at least two cases. First, if S (t) is a deterministic function. However, in this case, the probability of the realization of p [S (t)] = 1 , and therefore, the implementation of S (t) does not carry any information to the recipient,

The second case is when S (t) is a Gaussian process. The rule of composition of Gaussian laws applies here: when adding two Gaussian processes, the resulting process is also Gaussian, and the mathematical expectations and variances are summed up.

Since the signal S (t) and noise n (t) are independent, the average power of the total oscillation y (t) is determined by the sum of their powers: P _y = Ps + P _w .

Since noise has a Gaussian distribution, in order for the sum signal to have maximum entropy, it is necessary that the information or useful signal also have a Gaussian distribution. In this case, the performance R _y total fluctuations

y (t) = S (t) + n (t).

which represents a random process at the receiver input, is maximal and equals

_{<! [if! vml]> 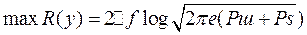<! [endif]>} (**)

Thus, based on the expressions (*) and (**), the throughput of a Gaussian communication channel is determined by the relation:

_{<! [if! vml]> 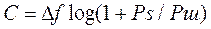<! [endif]>} bit / c (***)

The expression (***) represents the Shannon formula, widely known in communication theory, for the capacity of a continuous channel with Gaussian interference. This formula relates the width of the signal spectrum and the signal-to-noise ratio at the output of the communication channel (or at the receiver input) with the bandwidth of the continuous channel. It follows that the same bandwidth can be obtained with different ratios of pairs ∆f and Ps / Psh , that is, there is a possibility of a kind of exchange between the bandwidth and the signal-to-noise ratio to achieve a given channel bandwidth.

The Shannon formula also implies that the bandwidth can be increased by expanding the channel bandwidth, which is selected in accordance with the width of the signal spectrum. Hence the problem of synthesizing noise-like pulsed signals with a maximum width of the spectrum for transferring the maximum amount of information. These conclusions are a kind of bridge between information theory and signal coding theory.

Let us consider the limiting characteristics of throughput as ∆f changes. Considering that Psh = N ₀ * ∆f , where N ₀ is the spectral power density of white noise, the expression for throughput takes the form:

C = ∆f log ₂ (1 + Ps / N ₀ ∆f)

whence it is seen that monotonously depends on ∆f .

To find the maximum of this function, it suffices to find the limit

<! [if! vml]>

<! [endif]>

The ratio represents the limiting (maximum possible) value of the channel capacity at a given Ps / N ₀ ratio at the receiver input.

<! [if! vml]>

<! [endif]>
Denote

We will carry out the normalization of the bandwidth of the channel to the quantity h ₀ ²

The plot of normalized throughput versus ∆f / h ₀ ² is:

From the analysis of the graph it follows that the channel bandwidth quickly grows with the channel bandwidth expanded only in the initial part of the curve, where the signal power is greater than the noise power.

Note that, as studies show, the transmission rate in many existing communication systems is still too far from the theoretically possible values ​​of throughput.

11 2 Test questions .

1. What determines the transmission channel bandwidth with noises?

2. What should be done to pass a large amount of information through a very narrowband communication channel?

Topic 8 . Information encoding methods with compression .