Topic 4. Encoding of the source of discrete messages in the channel with interference. General principles of robust coding

Topic 4. Encoding of the source of discrete messages in the channel with interference. General principles of robust coding.

Lecture 5 .

5.1 Coding information for a channel with interference. Shannon's theorem for a noisy channel.

In this lecture we will proceed to the study of noise-resistant coding. It is intended for detecting and correcting errors of symbols in code words that occur in the transmission channel under the influence of interference and noise.

Consider first what mistakes occur most often and which less often.

To do this, consider the simplest channel model with interference. This is the Binary Symmetric Channel (SCMK). Channel symmetry means that the error probability, for 0 and for 1, is the same and equals p .

When transmitting information through the SCMK, the interference is able with some probability p to turn 0 into 1 or 1 into 0 . The transmission of information through the CJMS can be represented as the following graph, shown in Fig. 5.1:

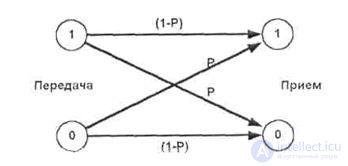
Fig.5.1

The calculation of the probability of distortion of the code word in the SCMK

Suppose a codeword consists of n binary characters. The probability of non-distortion of the entire code word, as it is easy to prove, is equal to:

The probability of distortion of one character (one-time error):

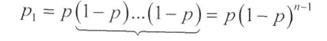
And for simultaneous distortion of several characters (multiple error)

Pr = p ^r * (1-p) ^(nr)

If the error probability is p <0.5 , (that is, the channel is not too bad), this expression implies that its probability decreases rapidly with increasing error rate (r) . Thus, small-time errors ( 1, 2, 3 characters) are much more likely than multiple errors. With them, and should be fought in the first place.

Encoding information for a channel with interference. Shannon's theorem for a noisy channel.

An error in a code combination appears when it is transmitted over a communication channel due to the replacement of one element by another under the influence of interference. For example, a 2-fold error occurs when replacing (distorting) two elements. For example, if code combination 01101 is taken as 01 01 1, then a double error occurs.

Recall the main characteristics of the communication channel. The bandwidth of a communication channel is defined as the maximum amount of information that a channel can miss per unit of time. Transmission speed is the amount of information that a channel actually passes per unit of time. That is, bandwidth is the maximum transfer rate.

Source performance is the amount of information generated by a source per unit of time.

The theory of robust coding is based on the results of research conducted by Shannon and formulated as a two-part theorem.

Shannon's theorem

1. For any performance of the source of the message, less than the bandwidth of the channel, there is a coding method that allows you to ensure the transfer of all the information generated by the source of messages, with an arbitrarily small probability of error.

2. There is no coding method that allows the transmission of information with an arbitrarily low probability of error if the performance of the message source is greater than the channel capacity.

From the theorem of Shannon, it follows that the interference in the channel does not impose restrictions on the accuracy of the transmission. The limitation is imposed only on the transmission rate at which arbitrarily high transmission accuracy can be achieved. That is, even with large noise in the channel, you can accurately, but slowly transmit information.

The theorem does not give us a method or method for constructing codes that ensure error-free transmission of information when exposed to interference, but it substantiates the fundamental possibility of such coding, which allows us to optimize the development of specific error-correcting codes.

At any finite information transfer rate, up to the channel capacity, an arbitrarily small probability of error is achieved only with an unlimited increase in the length of the encoded character sequences. Thus, error-free transmission in the presence of interference is only possible theoretically.

Ensuring the transfer of information with a very low probability of error and sufficiently high efficiency is possible only when encoding extremely long sequences of characters.

In practice, the accuracy of information transfer and the effectiveness of communication channels is limited by two factors:

1. the size and cost of equipment encoding / decoding;

2. the delay time of the transmitted message.

Varieties of error-correcting codes

Codes that provide the possibility of detecting and correcting errors, called immunity . These codes are used to:

1) error corrections - correction codes;

2) error detection.

Correction codes and error detection codes are based on the introduction of redundancy.

Noise-resistant codes are divided into two classes:

1) block;

2) continuous.

In the case of block codes, the coding procedure consists in converting or coding a sequence of information symbols of the input code word into a noise-resistant code word, but of a longer length. The large length of the error-correcting code is due to the introduction of additional or correction symbols when coding, which provide error detection and correction.

Only information symbols of the input word take part in coding operations and the output sequence of the error-correcting code word depends only on them.

A block is uniformly uniform if its length n remains constant for all information code words of length k characters,

Distinguish between systematic and non-systematic block codes. When coding with systematic codes, the output sequences consist of characters whose role can be clearly demarcated. These are information symbols that coincide with the symbols of the sequence, which is fed to the input of the channel coder, and redundant (check) characters, which are entered into the original sequence by the channel coder and are used to detect and correct errors.

When coding with non-systematic codes, it is impossible to divide the characters of the input sequence into information and verification.

Continuous - call such codes in which the introduction of redundant characters in the encoded sequence of information characters is carried out continuously, without dividing it into independent blocks. Continuous codes can also be separable and non-separable. We will not consider them.

5.2 General principles of the use of redundancy.

The ability of the code to detect and correct errors is due to the presence of redundant characters in it.

The figure below illustrates the construction principles of error-correcting codes.

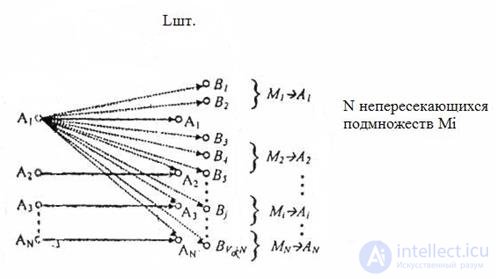
Fig.5.1

The figure illustrates the robust coding process by increasing the number of output code sequences associated with the original information code words.

The input of the encoder receives a sequence of k information binary symbols. At the output, it corresponds to a sequence of n binary symbols, and n> k .

There can be N = 2 ^k different input and L = 2 ⁿ different output sequences.

From the general number 2 ⁿ , the output sequences are only N = 2 ^k . sequences correspond to input. They are called allowed code combinations .

The remaining LN possible output sequences for the transmission are used. They are called forbidden code combinations .

Distortions of information in the process of transmission are reduced to the fact that some of the transmitted characters are replaced by others - incorrect.

Since each of the N = 2 ^k allowed combinations as a result of the interference can be transformed into any other, there are always L * N possible cases of transmission. This number includes:

1 ) N = 2 ^k cases of error free transmission;

2) N * (N-1) = 2 ^k (2 ^k -1) cases of transition to other allowed combinations, which corresponds to undetected errors;

3) N * (LN) = 2 ^k (2 ⁿ - 2 ^k ) cases of transition to unresolved combinations that can be detected.

Consequently, part of the detected erroneous code combinations of the total number of possible transmission cases is

N (LN) / (N * L) = (LN) / L = 1 -N / L.

Example: Determine the detecting ability of a code, each combination of which contains only one redundant character (n = k + l).

Solution : 1. The total number of output sequences is 2 ^{(k + 1)} , i.e. twice the total number of encoded input sequences.

2. For a subset of allowed code combinations, you can take, for example, a subset of combinations containing an even number of ones (or zeros).

3. When coding, one character (0 or 1) is added to each sequence of k information symbols such that the number of ones in the code combination is even. Receiving a word with an odd number of units translates the allowed code combination into a subset of forbidden combinations, which is found on the receiving side because of the odd number of units. Some of the errors identified are

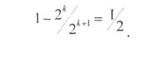
or 0.5 of the total number of possible code combinations.

Any decoding method can be considered as a rule for splitting the entire set of forbidden code combinations into N = 2 ^k disjoint subsets of Mj, each of which is associated with one of the allowed combinations. Upon receipt of the expanded combination belonging to the subset Mj , it is decided that the allowed combination Aj was transmitted; . The error will be corrected in cases where the resulting combination is really formed from Aj , i.e. Ln cases.

Total cases of transition to unresolved combinations

L (LN) = 2 ^k (2 ⁿ - 2 ^k ).

Thus, in the presence of redundancy, any code is able to correct errors.

The ratio of the number of erroneous code combinations corrected by code to the number of erroneous combinations detected is equal to

(LN) / N (LN) = 1 / N = 2 ^k .

The method of splitting into subsets depends on which errors should be corrected by a specific code.

Most of the codes developed are intended to correct mutually independent errors of a certain multiplicity and packets (or packets) of errors.

Mutually independent errors are such distortions in the transmitted codeword of characters, in which the probability of occurrence of any combination of distorted characters depends only on the number of distorted characters and the probability of distortion of a single character p .

With mutually independent errors, the probability of misrepresenting any g characters in an n-bit code combination, as already indicated for the binary symmetric channel model:

P _r = p ^r * (1-p) ^(nr)

where p is the probability of distortion of one character; r is the number of distorted characters; n is the number of binary symbols of the code word.

If we take into account that p << 1, then in this case errors of lower multiplicity are most probable. They should be detected and corrected first.

5.3 Relation of code correcting ability to code distance

With mutually independent errors, the most likely transition to a code combination that differs from this one in the smallest number of characters.

The degree of difference of any two code combinations is characterized by the distance between them in the Hamming sense, or simply by the code distance .

Code distance is expressed by the number of characters in which the combinations differ from one another, and is denoted by d .

To get the code distance between two binary code combinations, it is enough to count the number of units in the sum of these combinations modulo 2. For example

The minimum distance taken over all pairs of code-enabled code combinations is called the minimum code distance.

A more complete picture of the properties of the code is provided by the matrix of distances D , whose elements d _ij (i, j = 1,2, ..., n) are equal to the distances between each pair of all m allowed combinations.

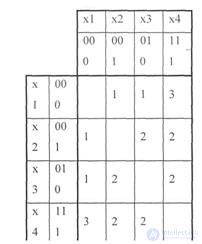
Example: To present a code X1 = 000 by a symmetric distance matrix ; X2 = 001; X3 = 010; X4 = 111

The decision . . The minimum code distance for the code is d = 1.

This follows from the consideration of the symmetric matrix of all possible code distances between code words.

Table 5.1

Decoding after reception is performed in such a way that the adopted code combination is identified with the allowed one that is located at the shortest code distance from it.

Such decoding is called maximum likelihood decoding .

5.4 Test questions.

1. What causes the effect of interference in the transmission channel?

2. What is the main practical conclusion from the theorem of Shannon for a noisy channel?

3. What is the main method of improving the noise immunity of codes?

4. What is code distance?

5. How does code distance relate to code noise immunity?